Практическое занятие №9-10. «Нормальные формы для формул алгебры высказываний (ч.1-2)»

Введем дополнительные (неэлементарные) логические операции:

• 
  Штрих Шеффера или антиконъюнкция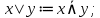
  
• 
  Стрелка Пирса (штрих Лукасевича) или антидизъюнкция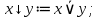
  
• 
  Сумма по модулю два (сумма Жегалкина) антиэквивалентность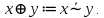
  

Таблица истинности для всевозможных булевых функций от двух переменных:

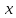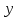		0		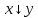		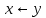		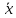		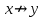		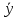		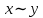		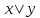	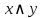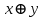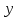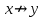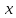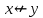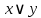1
0	0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
0	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	0	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

---

В формулах действует следующий порядок старшинства операций: отрицание «–» (если оно относится к одному высказыванию, например ), штрих Шеффера «| », стрелка Пирса « 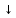», конъюнкция « 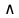», дизъюнкция « 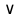», сумма по модулю два « 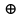», импликация « 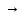», эквивалентность « ».

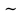Определение. 1. Нормальная форма логической формулы – это такакя форма записи логической формулы, при которой не содержится знаков импликации, эквивалентности и отрицания неэлементарных формул. Существует в двух видах:

• 
  конъюнктивная нормальная форма (КНФ) -- конъюнкция нескольких дизъюнкций.
  
• 
  дизъюнктивная нормальная форма (ДНФ) -- дизъюнкция нескольких конъюнкций.
  

Определение. 2. Совершенная конъюнктивная нормальная форма (СКНФ) -- это КНФ, удовлетворяющая трем условиям:

• 
  не содержит одинаковых элементарных дизъюнкций;
  
• 
  ни одна из дизъюнкций не содержит одинаковых переменных;
  
• 
  каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
  

Замечание. Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.

Правила построения СКНФ по таблице истинности:

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

Определение. 3. Совершенная дизъюнктивная нормальная форма (СДНФ) -- это ДНФ, удовлетворяющая трем условиям:

• 
  не содержит одинаковых элементарных конъюнкций;
  
• 
  ни одна из конъюнкций не содержит одинаковых переменных;
  
• 
  каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
  

Замечание. Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.

Правила построения СДНФ по таблице истинности:

---

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные.

Определение. 4. Карты Карно (схемы Вейча) это наглядное представление логической функции в виде карты, которая удобна для оптимизации.

Карты Карно представляют сбой определённую таблицу истинности обычно для двух, трёх и четырёх переменных и отличаются друг от друга способом обозначения строк и столбцов таблиц истинности.



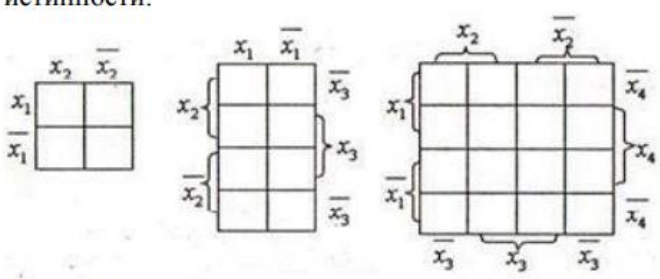
Расположение групп переменных x не имеет значения, необходимо лишь, чтобы каждая клетка отличалась от любой соседней лишь на одну переменную. Число клеток карты равно числу всевозможных интерпретаций переменных и в каждую клетку записывается значение формулы, соответствующее данной интерпретации переменных. Если какая-то из возможных комбинаций присутствует в СДНФ, то в соответствующей клетке ставится «1», в противном случае – « 0».

Логические схемы. Устройства, реализующие элементарные булевы функции, называют логическими элементами. Их входы соответствуют булевым переменным, а выход -- реализуемой функции.

В технике для обозначения логических элементов используют различные графические символы и названия, которые учитывают свойства и специфические особенности конкретных элементов. В теории принимаются упрощённые изображения в виде прямоугольников или других фигур, внутри которых помещаются условные названия или символы соответствующей функции (табл.1).

Таблица 1

Логические элементы, реализующие элементарные булевы функции

Функция	Нормальная форма	Контактная схема	Графическое изображение элемента	Название элемента
Отрицание				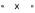Инвертор
Конъюнкция		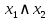		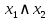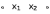Совпадение
Дизъюнкция	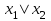		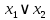	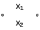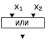Разделение
Импликация	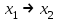		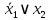	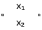Разделение с запретом
Эквивалентность	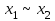		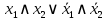	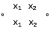Равнозначность
Отрицание импликации			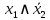	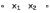Совпадение с запретом
Сумма по модулю 2	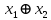		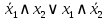	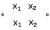Неравнозначность
Штрих Шеффера		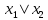		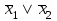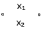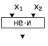Разделение с двумя запретами
Стрелка Пирса	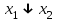		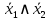	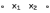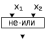Совпадение с двумя запретами

---

Например, на рис. 1a показана схема, реализующая функцию 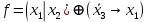, которая имеет три входных, один выходной и три внутренних узла. Обычно для упрощения узлы на схемах не изображаются и во избежание излишних пересечений входы рассредоточиваются с указанием связанных с ними переменных (рис.1.b).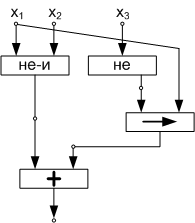



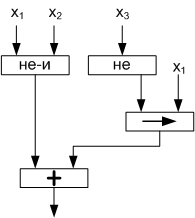
Рис. 1a Рис. 1b

Корректно построенные схемы должны удовлетворять следующим условиям:

• 
  не допускать замкнутых контуров, которые могут привести к неоднозначности сигналов на входах элементов;
  
• 
  любой вход элемента должен быть связан только с одним входом схемы или выходом другого элемента;
  
• 
  выходы элементов, не являющиеся выходами схемы и не связанные со входами других элементов, считаются лишними и исключаются из схемы.
  

1. 
   Выражая через конъюнкцию, дизъюнкцию и инверсию остальные связки, цепочкой равносильных преобразований заданную булеву формулу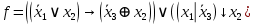 привести:
   a) к дизъюнктивной нормальной форме (ДНФ), по возможности сокращая количество литералов.
   b) к конъюнктивной нормальной форме (КНФ) также используя закон: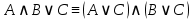
   .
   

Решение. a) Для начала, используя основные равносильности и приоритет операций избавимся от , 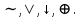Получим: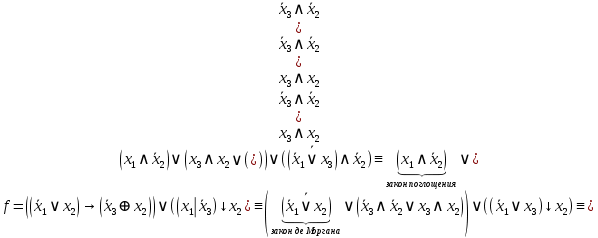

ДНФ:

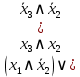
b) В полученной ДНФ раскроем скобки и сгруппируем так, чтобы получить КНФ:



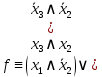
Вынесем общий множитель за скобки, поучим:

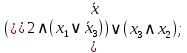
Раскроем скобки относительно дизъюнкции:

---

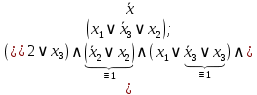
Так как 1 не влияет на конъюнкцию, то лишние множители можно опустить.

КНФ:

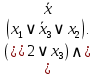
Ответ. а) ДНФ: b) КНФ:

2. 
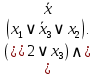
   Для заданной булевой формулы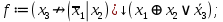 необходимо:
   

1. 
   построить таблицу истинности;
   
2. 
   вектору значений построить СДНФ и СКНФ;
   
3. 
   упростить выражение для СДНФ и СКНФ, используя карту Карно;
   
4. 
   составить схему устройства, реализующего заданную СДНФ и СКНФ после упрощения.
   

Решение.

1. 
   Построим таблицу истинности:
   

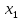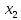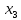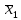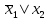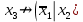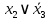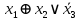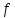0	0	0	1	1	0	1	1	0
0	0	1	1	1	0	0	0	1
0	1	0	1	0	0	1	1	0
0	1	1	1	0	1	1	1	0
1	0	0	0	1	0	1	0	1
1	0	1	0	1	0	0	1	0
1	1	0	0	1	0	1	0	1
1	1	1	0	1	0	1	0	1

---

Смотрите также файлы

• Классный час Государственные символы Российской Федерации.docx

• Открытый социальноэкономический колледж (ано по Открытый социальноэкономический колледж) Дисциплина безопасность жизнедеятельности.docx

• 3 Выполнен Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Выберите основную жалобу при болезнях желудка b. Тошнота, рвота Вопрос 4.docx

• Ооо мтц технология безопасности.doc

• Англия как главный спонсор нацистского режима.docx