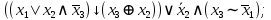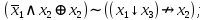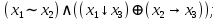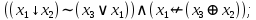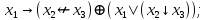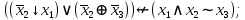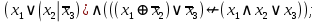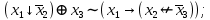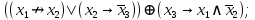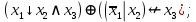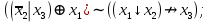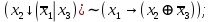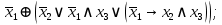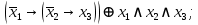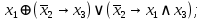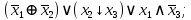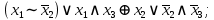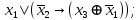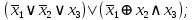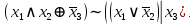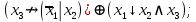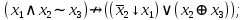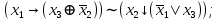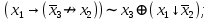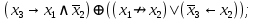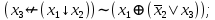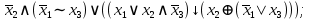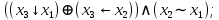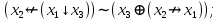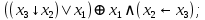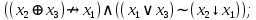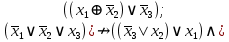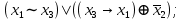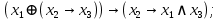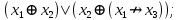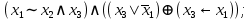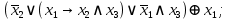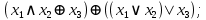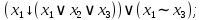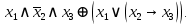Файл: Занятие 910. Нормальные формы для формул алгебры высказываний (ч. 12) Введем дополнительные (неэлементарные) логические операции.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 30

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



  1. Построение СДНФ:

Найдём наборы, на которых функция принимает истинное значение:
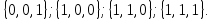
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
;
;


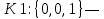
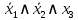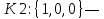
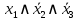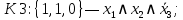
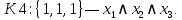
Объединим конъюнкции с помощью операции ИЛИ и получим СДНФ:



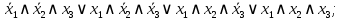
Построение СКНФ:

Найдём наборы, на которых функция принимает ложное значение: .
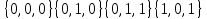В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:


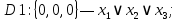
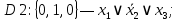
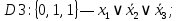
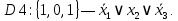
Объединим дизъюнкции с помощью операции И и получим СКНФ:



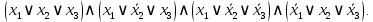
  1. Построим карту Карно для заданной функции, по ее вектор-значению: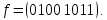


Для этого клетки наборов, на которых функция принимает значение 1, заполняется единицами; остальные клетки ­­­­– нулями.













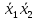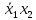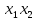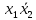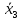0
0
1
1
0



1
0
1
0
1


00
01
11
10


Минимизация ДНФ: Выделим на карте Карно прямоугольные области из единиц наибольшей площади, и выпишем соответствующие им конъюнкции:

Область 1:























0
0
1
1
0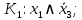







1
0
1
0
1







00
01
11
10






(так как переменные, которые не сохраняют свои значения на карте, в конъюнкции должны отсутствовать).

Область 2:


























0
0
1
1
0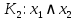
.






1
0
1
0
1










00
01
11
10











Область 3:






















0
0
1
1
0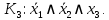







1
0
1
0
1







00
01
11
10






Объединим их с помощью операции и получим минимизированную ДНФ: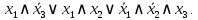



Минимизация КНФ: Выделим на карте Карно прямоугольные области из нулей наибольшей площади, и выпишем соответствующие им дизъюнкции ( причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием):

Область 1:






















0
0
1
1
0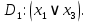







1
0
1
0
1







00
01
11
10






Область 2:






















0
0
1
1
0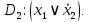







1
0
1
0
1







00
01
11
10






Область 3:






















0
0
1
1
0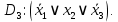







1
0
1
0
1







00
01
11
10






Объединим их с помощью операции и получим минимизированную КНФ:

.

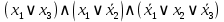  1. Составим схему устройства, реализующего заданную СДНФ и СКНФ после упрощения

Схема для минимальной ДНФ: .

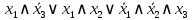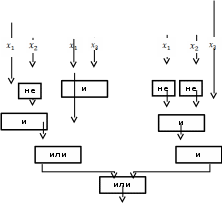
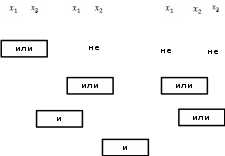
Схема для минимальной КНФ: .



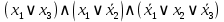Ответ. a) ;
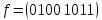b) СДНФ:
СКНФ: ;
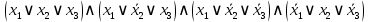c) МДНФ:
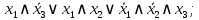
МКНФ: .

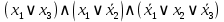Задачи для самостоятельного решения.



  1. Выражая через конъюнкцию, дизъюнкцию и инверсию остальные связки, цепочкой равносильных преобразований привести заданную булеву формулу:
    a) к дизъюнктивной нормальной форме (ДНФ), по возможности сокращая количество литералов.
    b) к конъюнктивной нормальной форме (КНФ) также используя закон:
    .












































  1. Для заданной булевой формулы необходимо:

    1. построить таблицу истинности;

    2. вектору значений построить СДНФ и СКНФ;

    3. упростить выражение для СДНФ и СКНФ, используя карту Карно;

    4. составить схему устройства, реализующего заданную СДНФ и СКНФ после упрощения.








































Смотрите также файлы