Добавлен: 09.11.2023
Просмотров: 47
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА»
(РУТ (МИИТ))
Кафедра: «Теплоэнергетика и водоснабжение на транспорте»
КУРСОВАЯ РАБОТА
По дисциплине: «ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА»
Тема: «Термодинамические циклы»
Рецензент Студент
К.т.н., доцент Драбкина Е.В. Соколов А.И.
Шифр: 1910-ц/ЭНб-2409
.
.
(подпись) (подпись)
.
.
(дата) (дата)
Москва 2022
Задача №1.
Для заданного кругового процесса (цикла), совершаемого рабочим телом в соответствии с табл. П1 и П3, определить:
Параметры состояния (P, V, T) в переходных точках;
Изменение внутренней энергии, энтальпии и энтропии в процессах;
Величину работы и теплоты для всех процессов (
,
, 
);Термический и относительный термический КПД;
Построить цикл в PV и TS координатах.
Исходные данные (последняя цифра шифра 9, вариант 1 в табл. П3):
м3/кг; 
ºС (
К); 
; 
кДж/кг.Процессы: 1-2 (dq=0, Р2>Р1), 2-3 (P=const), 3-4 (Т=const), 4-1 (v=const);
Объемный состав газа:
, 
,
.Решение.
Средняя молекулярная масса смеси газов равна сумме произведений объемных долей на молекулярные массы отдельных газов, составляющих смесь:
,
кг/кмоль, 
кг/кмоль, 
кг/кмоль.Получим:
кг/кмоль=0,03064 кг/моль.Газовую постоянную смеси газов определим по формуле:
,
(Дж/моль·К) – универсальная газовая постоянная.Получим:
Дж/кг·К.Далее определим изохорную и изобарную теплоемкость смеси. Для этого определим объемные теплоемкости каждого из компонентов смеси, используя формулу Майера. Имеем:
;
,где
- число степеней свободы молекулы каждого газа.
Дж/кг·К, 
Дж/кг·К, 
Дж/кг·К.Для
(
):
Дж/кг·К;
Дж/кг·К.Для
(
):
Дж/кг·К;
Дж/кг·К.Для
(
):
Дж/кг·К;
Дж/кг·К.Получим для смеси:
;
;
Дж/кг·К;
Дж/кг·К.Показатель адиабаты смеси:
.Далее определим параметры в основных точках цикла.
1-2: процесс адиабатный,
К , 
м3/кг, 
.Точка 1:
По уравнению Менделеева-Клапейрона:
;
;
Па=0,747 бар.Точка 2:
;
м3/кг.Из уравнения адиабаты следует, что:
;
;
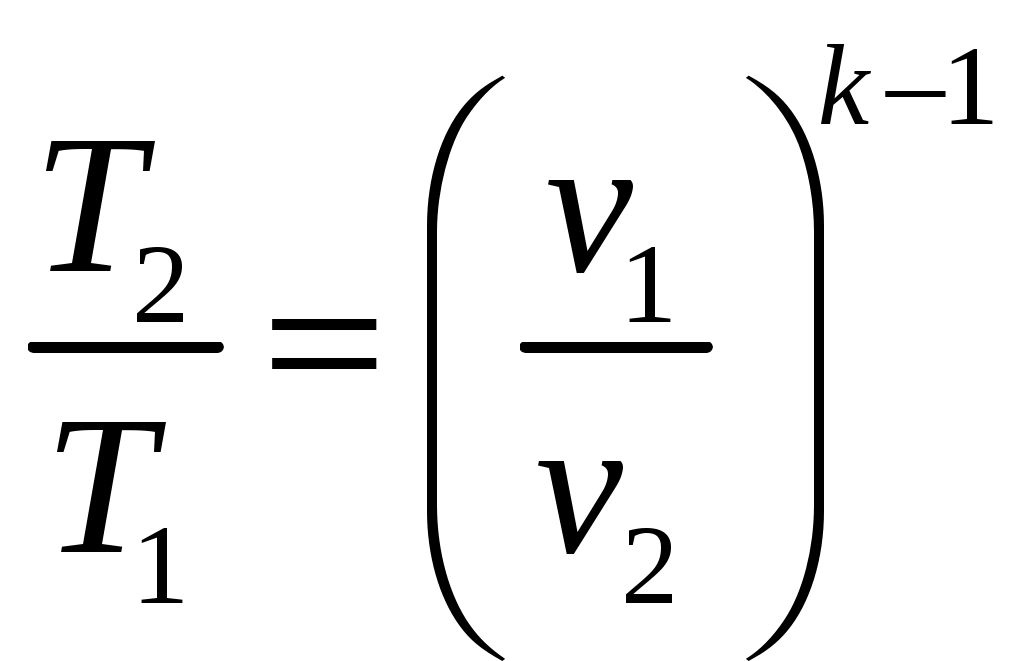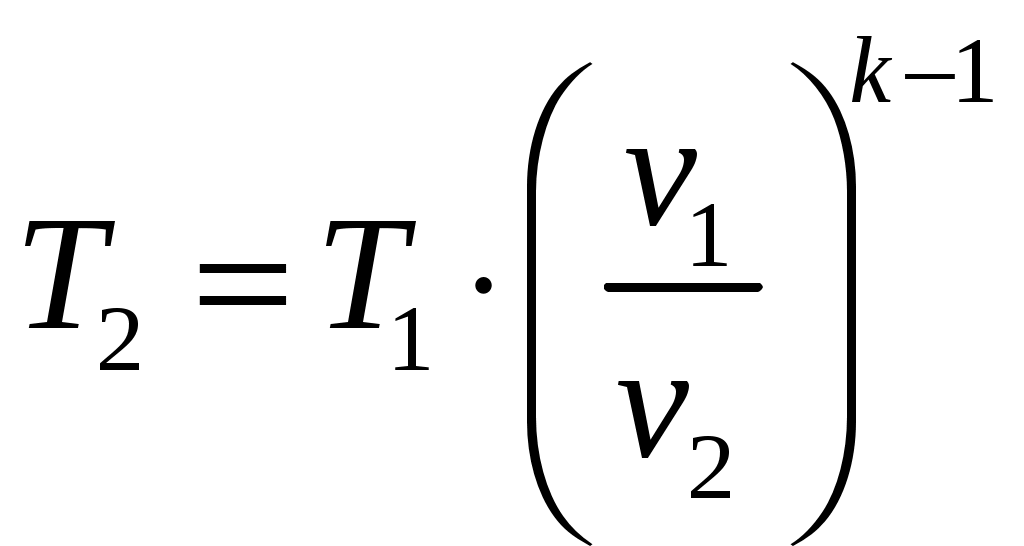К.По уравнению Менделеева-Клапейрона:
;
;
Па=23,039 бар.Для обратимого адиабатного процесса
, поэтому он также является изоэнтропным, поэтому:
и 
;
Дж/кг·°С.В адиабатном процессе работа определяется следующим образом:
;
Дж/кг= -339,7кДж/кг.
По второму закону термодинамики:
;
;
кДж/кг;
;
Дж/кг =468,7кДж/кг.Техническая работа:
кДж/кг.2-3: процесс изобарный,
бар, 
м3/кг, 
К, 
кДж/кг.Количество теплоты, сообщенное телу в изобарном процессе при постоянной теплоемкости, равно:
.Отсюда выразим температуру
:
;
К.
По уравнению Менделеева-Клапейрона:
;
;
м3/кг.Работа определяется следующим образом:
;
Дж/кг =192,6кДж/кг.Для изобарного процесса при постоянной теплоемкости изменение энтропии находится следующим образом:
;
Дж/кг·К;
Дж/кг·К.По второму закону термодинамики:
;
;
кДж/кг.Техническая работа:
кДж/кг.3-4: процесс изотермический,
К, 
бар, 
м3/кг, 
м3/кг.По уравнению Менделеева-Клапейрона:
;
;
Па=3,671 бар.Энтальпия и внутренняя энергия смеси газов в изотермическом процессе не меняются, то есть:
и 
.В изотермическом процессе количество подведенной к рабочему телу теплоты численно равно работе изменения объема: