Файл: Отчет по лабораторной работе 3 по дисциплине Динамика полета на тему Исследование системы улучшения устойчивости и управляемости бокового движения. Демпфер рыскания.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 36

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)
Кафедра №301

Отчет по лабораторной работе № 3

по дисциплине «Динамика полета»

на тему: «Исследование системы улучшения устойчивости и управляемости бокового движения. Демпфер рыскания»

Выполнили: студенты гр. М30-301С-18

Сазонова Е.В, Романычев А.В., Воропаева С.М.

Принял: доцент кафедры 301

______________ П.В. Мулин.

Москва, 2021 г.

Постановка задачи исследования:

  1. Создать схему имитационного моделирования изолированного движения рыскания в среде MATLAB-SIMULINK. Отобразить схему в отчете.

  2. Построить графики реакции на единичное ступенчатое воздействие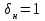 по координатам 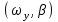и .

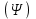  3. Создать схему имитационного моделирования изолированного движения рыскания с демпфером в среде MATLAB-SIMULINK. Отобразить схему моделирования в отчете.

  4. Для желаемого значения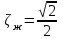 из уравнения (1) найти значение .

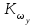  5. Выбрать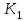 из условия обеспечения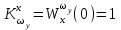

  6. Построить графики реакции на единичное ступенчатое воздействие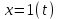 по координатам 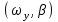и 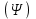для двух случаев:





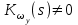
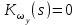
  1. Определить перерегулирование, время переходного процесса .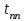

Исходные данные:


Значения параметров объекта управления взять из таблицы











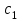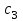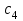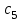0.3
0.4
0.7
0.1
0.03



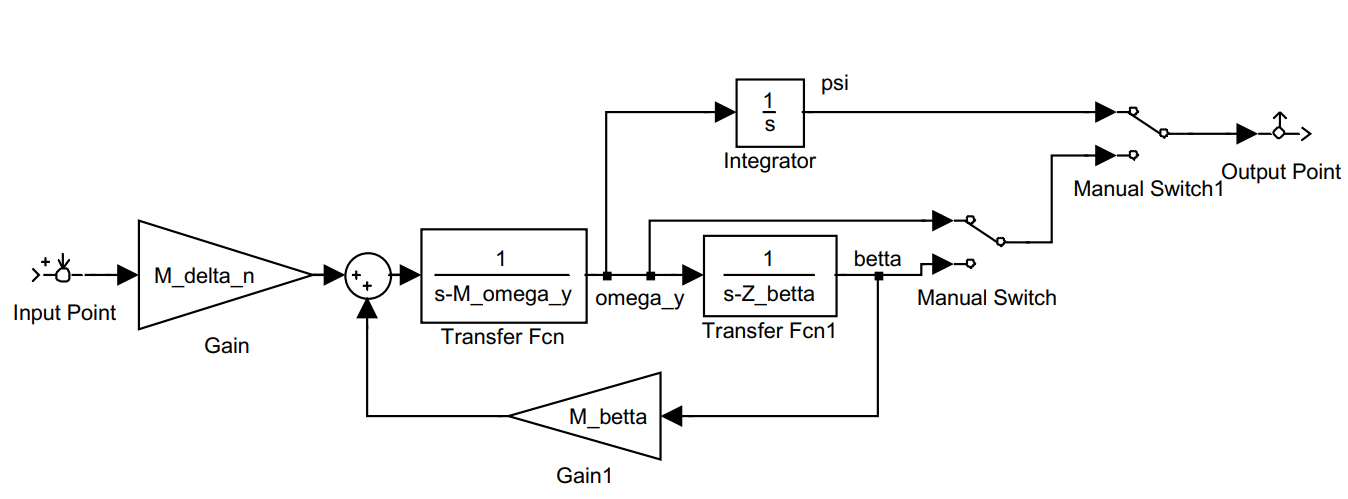
Рисунок 1. Simulink-модель схемы имитационного моделирования изолированного движения рыскания



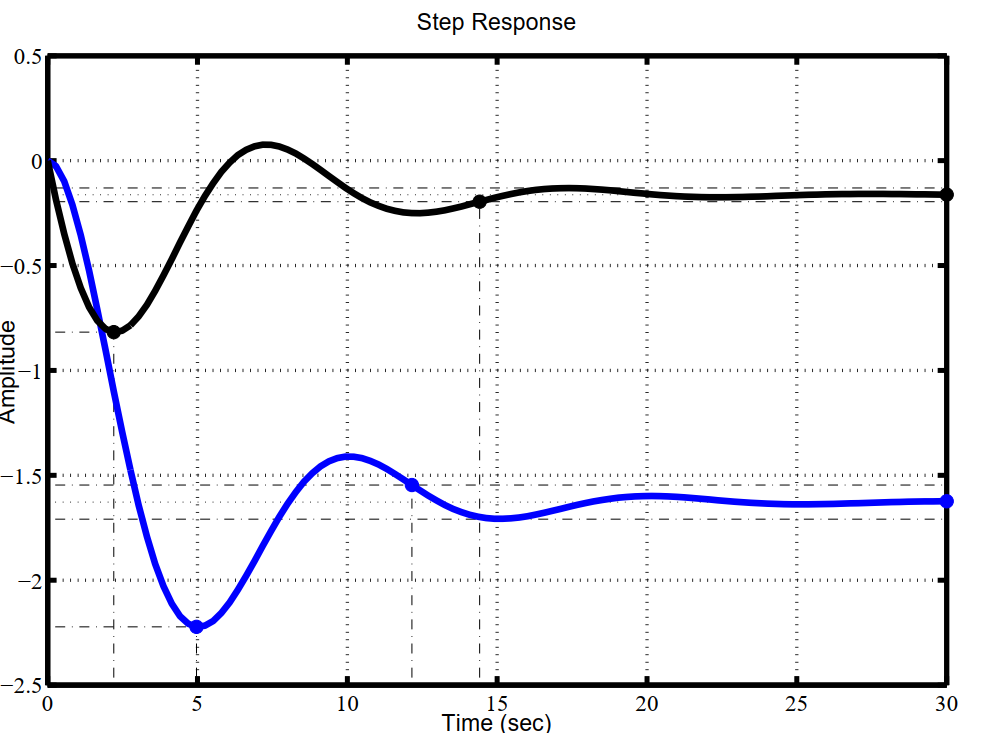
Рисунок 2. Графики переходных процессов по координатам



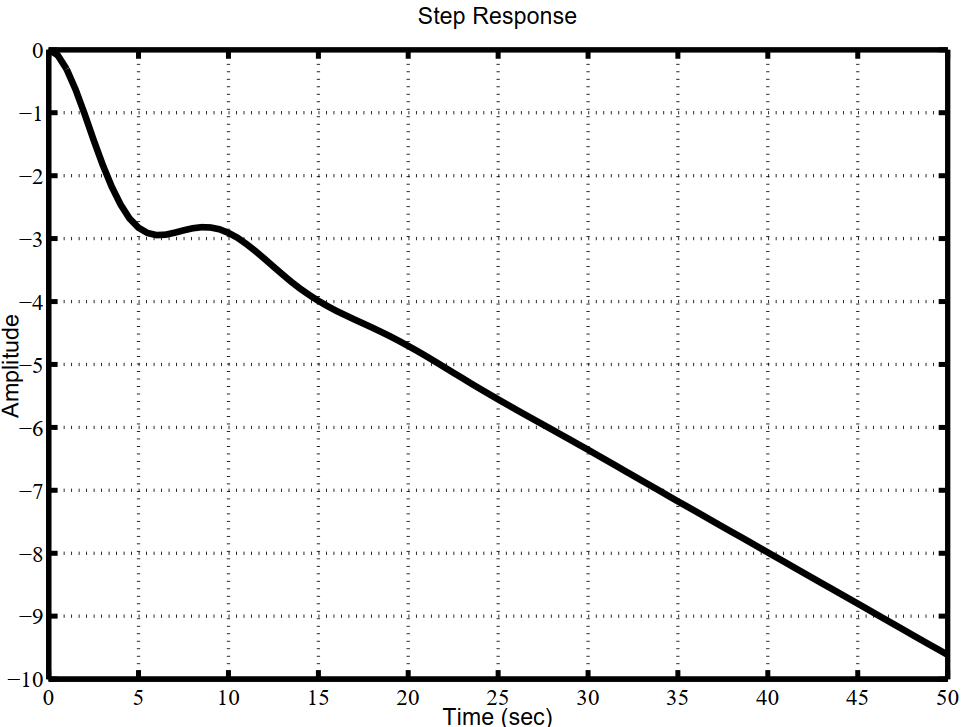
Рисунок 3. График переходного процесса по координате



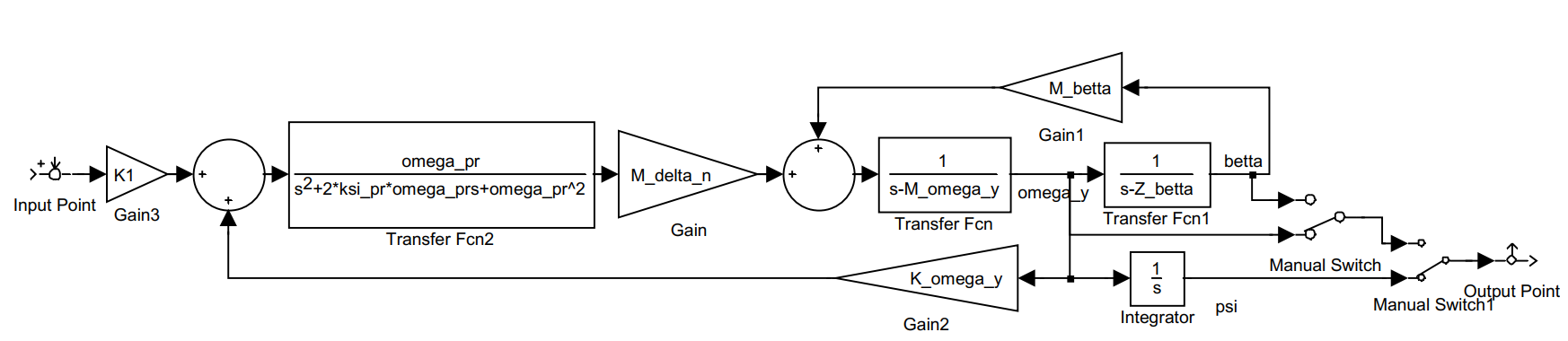
Рисунок 4. Simulink-модель схемы имитационного моделирования изолированного движения рыскания с демпфером

Из уравнения 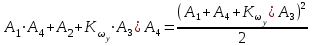для желаемого значения 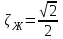найдем значение .

Из условия 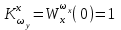найдем значение .

Список команд:

syms K_omega_y

A1=0.3;

A2=0.4;

A3=0.7;

A4=0.1;

A7=0.03;

M_delta_n=-A3;

M_omega_y=-A1;

M_betta=-A2;

Z_betta=-A4;

K_omega_y=vpa(solve(A1*A4+A2+K_omega_y*A3*A4-((A1+A4+K_omega_y*A3)^2)/2), 4)

Полученный результат:

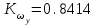
Из условия обеспечения найдем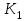


Список команд:

syms K_omega_y K1 s

A1=0.3;

A2=0.4;

A3=0.7;

A4=0.1;

A7=0.03;

M_delta_n=-A3;

M_omega_y=-A1;

M_betta=-A2;

Z_betta=-A4;

omega_pr=20;

ksi_pr=0.707;

K_omega_y=0.8414

A_pr=omega_pr^2;

B_pr=s^2+2*ksi_pr*omega_pr*s+omega_pr^2;

W_pr=A_pr/B_pr;

W1=1/(s-M_omega_y);

W2=1/(s-Z_betta);

W_omega_y=collect(K1*W_pr*M_delta_n*W1/(1-W1*W_pr*M_delta_n*K_omega_y-W1*W2*M_betta),s)

W_omega_y=subs(W_omega_y,s,0)

K1=vpa(solve(W_omega_y-1),4)

Полученный результат:



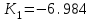
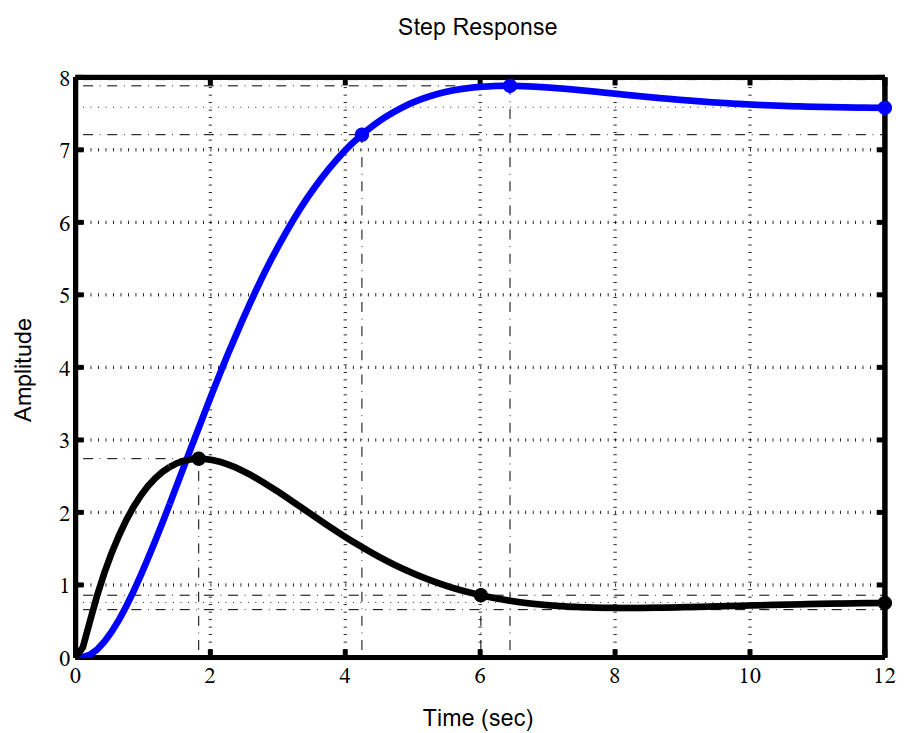
Рисунок 4. Графики переходных процессов по координатам при



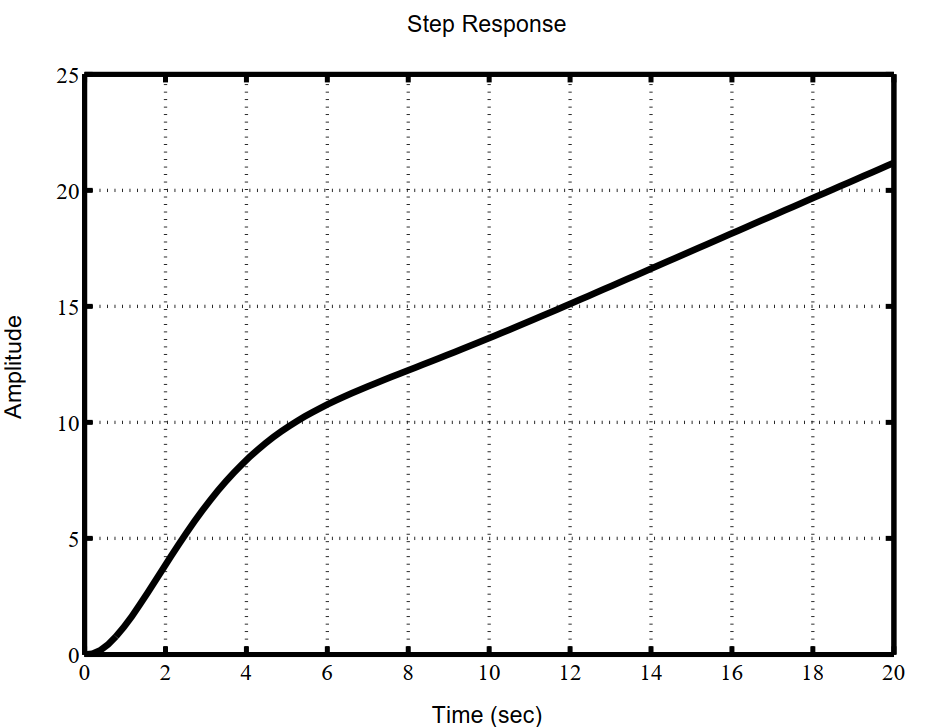
Рисунок 5. График переходного процесса по координате при



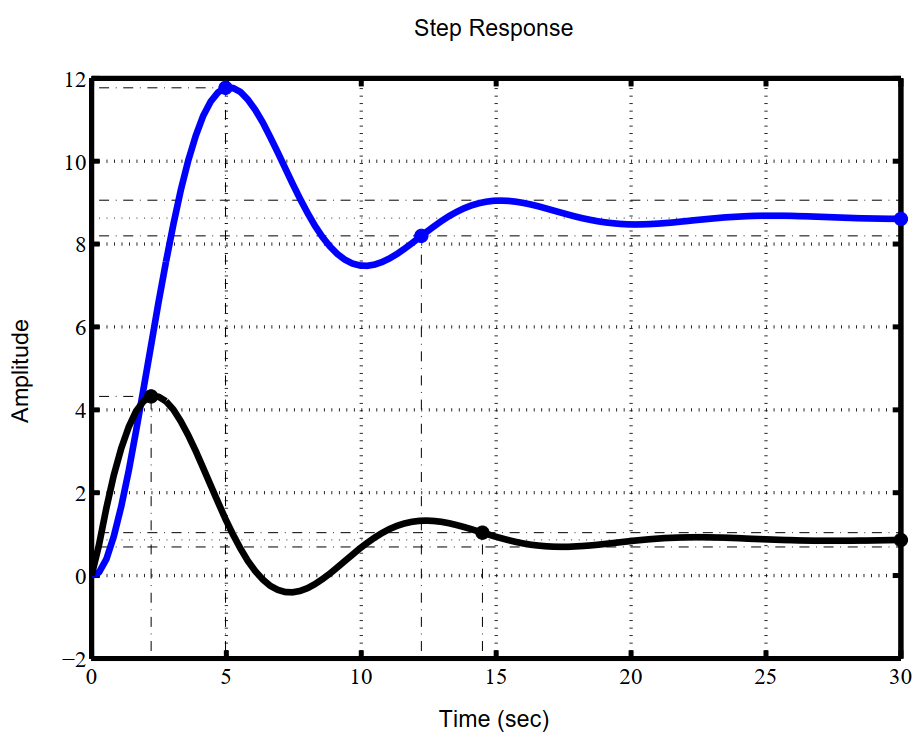
Рисунок 6. Графики переходных процессов по координатам при



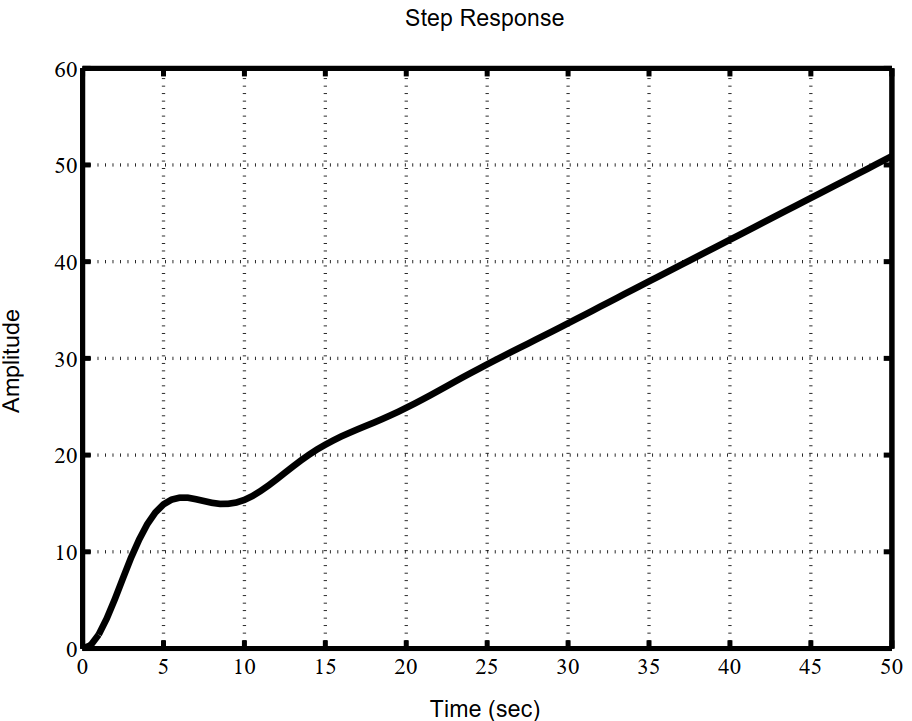
Рисунок 7. График переходного процесса по координате при

Смотрите также файлы