Файл: Решение Выборочная доля равна, где m число фирм с затратами на рекламу 5 и менее у е. n объем выборки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 8
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАДАНИЕ 8.
Вариант 1. Данные по фирмам 1-10 являются 10%-ной бесповторной выборкой. Для генеральной совокупности определите пределы, в которых могут находиться:
- доля фирм с затратами на рекламу 5 и менее у.е.;
- средний объем затрат на рекламу.
Расчеты выполнить с вероятностью 0,954.
Рассчитать численность выборки, если ошибку доли увеличить на 15%.
Решение:
1. Выборочная доля равна:
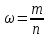 ,
,где m – число фирм с затратами на рекламу 5 и менее у.е.;
n – объем выборки.
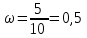
Определим среднюю ошибку выборки:
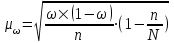

Предельная ошибка выборки:
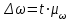
Т.к. Р=0,954, то t=2
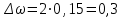
Доверительные пределы доли предприятий:
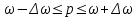
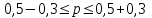
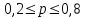
Вывод. С вероятностью 0,954 можно утверждать, что в генеральной совокупности фирм доля фирм с затратами на рекламу 5 и менее у.е. будет находиться в пределах от 20% до 80%.
2. Формула расчета средней ошибки выборочной средней следующая:
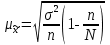 ,
,где N – число единиц в генеральной совокупности;
n – число единиц в выборочной совокупности.

Предельная ошибка выборки:
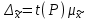
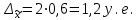
Доверительные интервалы средней:
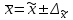 ,
,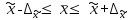 ,
,где
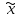
– выборочная средняя,
 – генеральная средняя.
– генеральная средняя.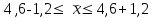
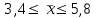
Вывод. На основании проведенного выборочного обследования фирм с вероятностью 0,954 можно утверждать, что для генеральной совокупности фирм средний объем затрат на рекламу находится в пределах от 3,4 у.е. до 5,8 у.е.
3. Необходимый объем выборочной совокупности вычислим по формуле:
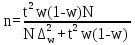

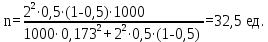
Объем выборки должен быть не менее 33 фирм, чтобы с вероятностью Р=0,95 гарантировать, что ошибка не превысит 17,3% .