МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра АИУС

Расчетно-графическое задание

Дисциплина: Системы обнаружения, наведения и ориентации летательных аппаратов

Тема: Геометрические преобразования изображений

Факультет: ЛА Преподаватель:

Группа: АУМ-11 Борисова И.В.

Студент:

Шабалов С.Д.

Новосибирск, 2022

1. 
   ЦЕЛЬ РАБОТЫ
   

Средствами MATLAB выполнить преобразование поворота и масштабирования с интерполяцией по ближайшему соседу и билинейной интерполяцией. Моделирование выполнить для различных изображений, реальных и тестовых и разных параметров преобразования (углов и коэффициентов масштабирования). Проанализировать полученные результаты на расхождение с исходными изображениями.

Расчетно-графическое задание должно содержать: титульный лист, краткое теоретическое изложение по теме аффинных преобразований и моделирования в MATLAB, текст программы, исходные изображения, полученные результаты, выводы.

2. 
   ТЕОРИЯ
   

Преобразование плоскости называется аффинным, если

• 
  оно взаимно однозначно;
  
• 
  образом любой прямой является прямая.
  

Преобразование называется взаимно однозначным, если

• 
  разные точки переходят в разные;
  
• 
  в каждую точку переходит какая-то точка.
  

Общий вид аффинного преобразования - матрица 3x3, последний столбец которой равен ( 0 0 1 )^T, задает аффинное преобразование плоскости:

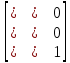
По одному из свойств, аффинное преобразование можно записать в виде:

f(x) = x * R + t,

где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом:

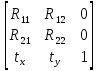
При аффинном преобразовании площади всех фигур изменяются в |R|.

Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Разберем более подробно природу этой матрицы и возможности, которые она нам дает.

---

Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R_1,1, R_1,2), вектор (0, 1) переходит в (R_2,1, R_2,2). Новый базис — это строки матрицы R.

Сжатие/растяжение:

Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (a_x * x, a_y * y). Матрица преобразования запишется следующим образом:

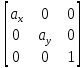
где   a_x – растяжение по оси x,

a_y – растяжение по оси y.

Поворот:

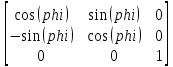
При угле phi = π эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования).

Параллельный перенос:

Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом: 

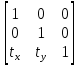
Кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос.
Image Processing Toolbox™ предоставляет полный набор стандартных алгоритмов и приложений для рабочего процесса для обработки изображений, анализа, визуализации и разработки алгоритмов. Вы можете выполнять сегментацию изображений, улучшение изображения, шумоподавление, геометрические преобразования и регистрацию изображений, используя глубокое обучение и традиционные методы обработки изображений. Набор инструментов поддерживает обработку 2D, 3D и изображений произвольного размера. Приложения Image Processing Toolbox позволяют автоматизировать обычные рабочие процессы обработки изображений. Вы можете интерактивно сегментировать данные изображений, сравнивать методы регистрации изображений и выполнять пакетную обработку больших наборов данных. Функции визуализации и приложения позволяют просматривать изображения, 3D-объемы и видео.

Базовой структурой данных в MATLAB® является массив, упорядоченный набор реальных или сложных элементов. Этот объект естественным образом подходит для представления изображений, вещественных упорядоченных наборов данных о цвете или интенсивности.

MATLAB хранит большинство изображений в виде двумерных матриц, в которых каждый элемент матрицы соответствует одному дискретному пикселю в отображаемом изображении. (Пиксель является производным от элемента изображения и обычно обозначает единственную точку на дисплее компьютера.) Например, изображение, состоящее из 200 строк и 300 столбцов с разноцветными точками, будет сохранено в MATLAB в виде матрицы размером 200 на 300.

---

Некоторые изображения, такие как изображения truecolor, представляют изображения с использованием трехмерного массива. В изображениях truecolor первая плоскость в третьем измерении представляет интенсивность красных пикселей, вторая плоскость представляет интенсивность зеленых пикселей, а третья плоскость представляет интенсивность синих пикселей. Это соглашение делает работу с изображениями в MATLAB аналогичной работе с любым другим типом числовых данных и делает всю мощь MATLAB доступной для приложений обработки изображений.

Программное обеспечение Image Processing Toolbox™ определяет несколько основных типов изображений включая двоичные изображения, изображения в оттенках серого, изображения истинного цвета, многоспектральные изображения и изображения ярлыков. Эти типы изображений определяют способ, которым MATLAB® интерпретирует элементы массива как значения интенсивности пикселей.

3. 
   ХОД РАБОТЫ
   

Текст программы:

% шахматнаядоскабелая

check = checkerboard(64) > 0.5;

imshow (check)

imwrite(check, 'check.png') % изображение 512x512

F = imread(' '); % перебор реальных и тестовых изображений

f = im2double(F);

% билинейная интерполяция (по умолчанию)

t_30 = [cos(pi/6) sin(pi/6) 0; -sin(pi/6) cos(pi/6) 0; 0 0 1]; % матрица поворота на 30град

tform_30 = maketform('affine', t_30);

Ft_30 = imtransform(F, tform_30); % поворот изображения на 30град

figure; imshow(Ft_30)

t_135 = [cos(3*pi/4) sin(3*pi/4) 0; -sin(3*pi/4) cos(3*pi/4) 0; 0 0 1]; % матрицаповоротана 135град

tform_135 = maketform('affine', t_135);

Ft_135 = imtransform(F, tform_135); % поворотизображенияна 135град

figure; imshow(Ft_135)

t_scale_dif = [0.8 0 0; 0 0.6 0; 0 0 1]; % матрицамасштабирования (разныймасштабпоосям)

tform_scale_dif = maketform('affine',t_scale_dif);

Ft_scale_dif = imtransform(F, tform_scale_dif); % масштабированиеизображения

i = (size(F,1)-size(Ft_scale_dif,1))/2;

j = (size(F,2)-size(Ft_scale_dif,2))/2;

Ft_scale_dif_full = padarray(Ft_scale_dif, [i j], 'both'); % заполнениекраев

figure; imshow(Ft_scale_dif_full)

t_scale = [0.6 0 0; 0 0.6 0; 0 0 1]; % матрица масштабирования (одинаковый масштаб)

tform_scale = maketform('affine',t_scale);

Ft_scale = imtransform(F, tform_scale); % масштабированиеизображения

i = (size(F,1)-size(Ft_scale,1))/2;

j = (size(F,2)-size(Ft_scale,2))/2;

Ft_scale_full = padarray(Ft_scale, [i j], 'both');

figure; imshow(Ft_scale_full)

% интерполяция по ближайшему соседу

Ft_30_n = imtransform(F, tform_30, 'nearest'); % поворот изображения на 30град

figure; imshow(Ft_30_n)

---

Ft_135_n = imtransform(F, tform_135, 'nearest'); % поворот изображения на 135град

figure; imshow(Ft_135_n)

Ft_scale_dif_n = imtransform(F, tform_scale_dif, 'nearest'); % масштабированиеизображения

i = (size(F,1)-size(Ft_scale_dif_n,1))/2;

j = (size(F,2)-size(Ft_scale_dif_n,2))/2;

Ft_scale_dif_full_n = padarray(Ft_scale_dif_n, [i j], 'both'); % заполнениекраев

figure; imshow(Ft_scale_dif_full_n)

Ft_scale_n = imtransform(F, tform_scale, 'nearest'); % масштабированиеизображения

i = (size(F,1)-size(Ft_scale_n,1))/2;

j = (size(F,2)-size(Ft_scale_n,2))/2;

Ft_scale_full_n = padarray(Ft_scale_n, [i j], 'both');

figure; imshow(Ft_scale_full_n)
Результаты программы:

Рис. 1. check.png
Рис. 2. Поворот на 30 градусов, билинейная интерполяция	Рис. 3. Поворот на 30 градусов, интерполяция по ближайшим соседям
Рис. 4. Поворот на 135 градусов, билинейная интерполяция	Рис. 5. Поворот на 135 градусов, интерполяция по ближайшим соседям
Рис. 6. Масштабирование с разным масштабом, билинейная интерполяция	Рис. 7. Масштабирование с разным масштабом, интерполяция по ближайшему соседу
Рис. 8. Масштабирование с одинаковым масштабом, билинейная интерполяция	Рис. 9. Масштабирование с одинаковым масштабом, интерполяция по ближайшему соседу
Рис. 10. ракушки.png
Рис. 11. Поворот на 30 градусов, билинейная интерполяция	Рис. 12. Поворот на 30 градусов, интерполяция по ближайшим соседям
Рис. 13. Поворот на 135 градусов, билинейная интерполяция	Рис. 14. Поворот на 135 градусов, интерполяция по ближайшим соседям
Рис. 15. Масштабирование с разным масштабом, билинейная интерполяция	Рис. 16. Масштабирование с разным масштабом, интерполяция по ближайшему соседу
Рис. 17. Масштабирование с одинаковым масштабом, билинейная интерполяция	Рис. 18. Масштабирование с одинаковым масштабом, интерполяция по ближайшему соседу

---

ВЫВОД
Анализируя рисунки (результаты применения интерполяции) можно сделать вывод, что при применении билинейной интерполяции происходит сглаживание изображения, если сравнивать его с оригиналом. В случае интерполяции по ближайшему соседу на выходе получаем изображение с увеличенной резкостью.

Можно заметить полосы, которые появляются в случае изменения масштаба (на шахматной доске от светло серого до черного).

Если поворот изображения не кратен 90⁰, то можно заметить, что происходит потеря пикселей, отсюда можно сделать вывод, что нужно избегать потери пикселей, используя дополнительные методы обработки изображений

---

Смотрите также файлы

• Samdu ozbekiston fenlandiya pegagigika inisitetuti aniqtabiy fanlar va jismoniy madaniyat fakulteti matimatikainformatika talim yonalishi 109 guruh talabalarining malumotlari.docx

• Расчёт и проектирование балочной стрелы.docx

• Сетевые информационные технологии.pdf

• Жалпы орта білім беру дегейіні 1011сыныптарына арналан аза дебиеті пнінен.doc

• Таныстырылымды зара алыптастырушы баалау проформасы.docx