Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Омский государственный технический университет»

ЛАБОРАТОРНАЯ РАБОТА № 7

«Теория электрических цепей»

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ПЕРИОДИЧЕСКИХ НЕСИНУСОИДАЛЬНЫХ СИГНАЛОВ


Выполнили:

Исаева Е.В.

Загребнев И.В.

Группа: ПР-222

Проверил: Гонтовой Е.А.

Омск, 2023

Цель работы: Изучение способа представления периодических несинусоидальных сигналов в виде совокупности гармонических составляющих (дискретного частотного спектра).

Исходные данные:

Амплитуда исследуемого сигнала e_m = 3+N, гдеN =1, e_m = 4 [В];

Частота исследуемого сигнала f =f_D = 1100 [Гц].


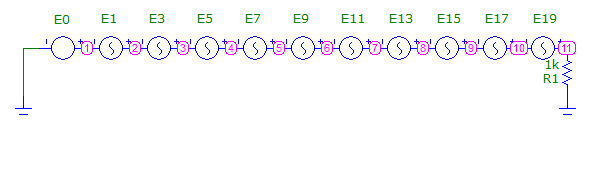
Рис.1. Схема исследуемой электрической цепи

1. 
   Произведем теоретический расчёт дискретного частотного спектра сигнала, для этого необходимо определить постоянную составляющую сигнала и амплитуды первых 10 гармоник:
   

E0 = e_m/2=2 [В]

E1 = 2 * e_m/π = 2,546479 [В]

E3 = 2 * e_m/3*π = 0,848826 [В]

E5 = 2 * e_m/5*π = 0,509296 [В]

E7 = 2 * e_m/7*π = 0,363783 [В]

E9 = 2 * e_m/9*π = 0,282942 [В]

E11 = 2 * e_m/11*π = 0,231498 [В]

E13 = 2 * e_m/13*π = 0,195883 [В]

E15 = 2 * e_m/15*π = 0,169765 [В]

E17 = 2 * e_m/17*π = 0,149793 [В]

E19 = 2 * e_m/19*π = 0,134025 [В]

2. 
   В соответствии с формулой: ψ_k = 0 для k = 1, 2, 3, …; все гармоники имеют нулевые начальные фазы:
   

ψ₁ = ψ₃ = ψ₅ = ψ₇ = ψ₉ = ψ₁₁ = ψ₁₃ = ψ₁₅ = ψ₁₇ = ψ₁₉ = 0
Определим частоты первых 10 гармоник:

f1 = f = 390 [Гц]	f11 = 11∙f = 11∙390 = 4290 [Гц]
f3 = 3∙f = 3∙390 = 1170 [Гц]	f13 = 13∙f = 13∙390 = 5070 [Гц]
f5 = 5∙f = 5∙390 = 1950 [Гц]	f15 = 15∙f = 15∙390 = 5850 [Гц]
f7 = 7∙f = 7∙390 = 2730 [Гц]	f17 = 17∙f = 17∙390 = 6630 [Гц]
f9 = 9∙f = 9∙390 = 3510 [Гц]	f19 = 19∙f = 19∙390 = 7410 [Гц]

---

Табл.1. Результаты расчета амплитуды и частот первых 10 гармоник

Гармоники	Амплитуда гармоники, В	Частота гармоники Гц	Начальная фаза гармоники, град.
0	2	0	-
1	2,546479	390	0
3	0,848826	1170	0
5	0,509296	1950	0
7	0,363783	2730	0
9	0,282942	3510	0
11	0,231498	4290	0
13	0,195883	5070	0
15	0,169765	5850	0
17	0,149793	6630	0
19	0,134025	7410	0

3. 
   В результате моделирования, было получено три осциллограммы:
   

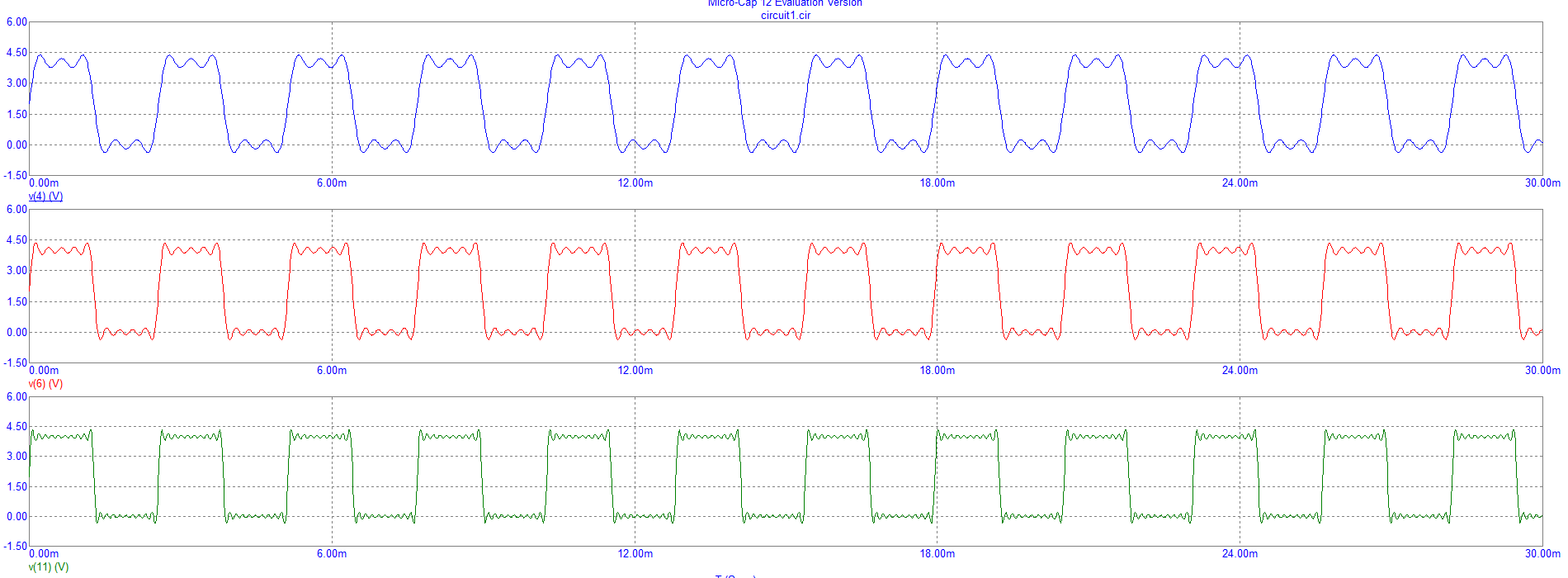
Рис.2. Осциллограммы трех, пяти и десяти гармоник.
Первая осциллограмма показывает сигнал трех гармоник.

Вторая осциллограмма показывает сигнал пяти гармоник.

Третья осциллограмма показывает сигнал десяти гармоник.
Вывод

Был изучен способ представления периодических несинусоидальных сигналов в виде совокупности гармонических составляющих (дискретного частотного спектра). Полученные данные показали, что чем больше гармоник в дискретном частотном спектре, тем точнее восстановление исследуемого сигнала.

---

Смотрите также файлы

• Упражнения по боевому развертыванию боевых расчетов.docx

• Виды съемок Репортажная съемка.pptx

• Отчет по учебной практике по специальности 38. 02. 03 Операционная деятельность в логистике уп. 01. 01 по планированию и организации логистического.docx

• Научный стиль текста Сфера функционирования научного текста.docx

• Общая теория связи.docx