Файл: исследование устойчивости замкнутой цифровой системы управления по курсу цифровые системы управления.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 14
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА №31
ПРЕПОДАВАТЕЛЬ
| доцент | | | | Бойков В.И. |
| должность, уч. степень, звание | | подпись, дата | | инициалы, фамилия |
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №5
«ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЗАМКНУТОЙ ЦИФРОВОЙ СИСТЕМЫ УПРАВЛЕНИЯ»
по курсу: ЦИФРОВЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
| СТУДЕНТ ГР. № | 3023 | | 11.05.2023 | | Хорубко А.Д. | |
| | номер группы | | подпись, дата | | инициалы, фамилия | |
Санкт-Петербург
2023
Цель работы
Изучение методов исследования устойчивости замкнутой цифровой системы и расчета цифровой системы с конечной длительностью переходных процессов. Исследование влияния величины шага квантования по времени на динамические свойства системы.
Исходные данные
Вариант 9
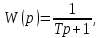
где:
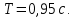
Ход работы
Вывод аналитически дискретную передаточную функцию G(z) инерционного звена первого порядка, включенного по схеме с идеальным квантователем с периодом h и фиксатором нулевого порядка на входе, использовав приближенный метод Эйлера. Параметры передаточной функции W(p) инерционного звена представлены ниже.
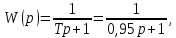
где:
Заменяется параметр
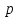на следующее выражение: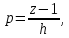
где:
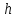- период квантования.Таким образом, дискретная передаточная функция G(z) инерционного звена первого порядка имеет вид:
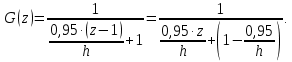
Вывод аналитически дискретную передаточную функцию H(z) замкнутой по выходу цифровой системы с передаточной функцией прямого тракта G(z) и пропорциональным регулятором с коэффициентом передачи К.
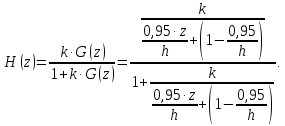
Использовав корневой критерий устойчивости линейной дискретной системы с передаточной функцией H(z) требуется получить аналитическую зависимость коэффициента передачи К регулятора от параметров передаточной функции и периода квантования h системы.
В полученном выражении
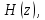знаменатель приравнивается к нулю и выводится переменная z.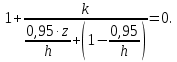
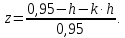
Определение
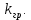Тогда, в этом случае 
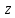будет принимать граничные значения от -1 до 1.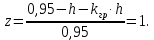
Таким образом,
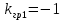
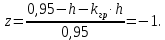
Таким образом,
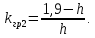
При
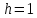коэффициента передачи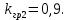 
Определение оптимальный коэффициент передачи. В этом случае выражение имеет вид:
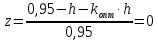
Таким образом,
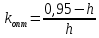
При
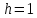
коэффициента передачи
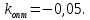
Точное выражение дискретного аналога передаточной функции инерционного звена первого порядка, включенного по схеме с идеальным квантователем с периодом h и фиксатором нулевого порядка на входе, имеет вид
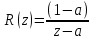,где:
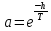- параметр передаточной функции.Вывод аналитически дискретную передаточную функцию F(z) замкнутой по выходу цифровой системы с передаточной функцией прямого тракта R(z) и пропорциональным регулятором с коэффициентом передачи К.
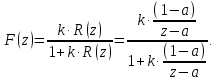
Используя корневой критерий устойчивости линейной дискретной системы с передаточной функцией F(z) получить аналитическую зависимость коэффициента передачи К регулятора от параметра передаточной функции Т и периода квантования h системы.
В полученном выражении
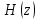, знаменатель приравнивается к нулю и выводится переменная z.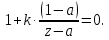
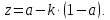
Определение
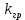. Тогда в этом случае 
будет принимать граничные значения от -1 до 1.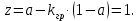
Таким образом,
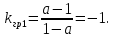
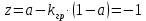
Таким образом,
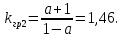
Определение оптимального коэффициента передачи. В этом случае выражение имеет вид:
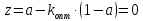
Таким образом,
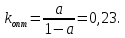
Собрана схема исследования замкнутой цифровой системы (Рисунок 1). Верхняя часть схемы представляет модель исследуемой дискретной системы. Нижняя часть схемы содержит модель ее точного дискретного аналога. Сравнение реакций обоих моделей реализована путем вычисления ошибки (разности реакций), которая подана на второй вход осциллоскопа для визуального контроля. Это разность должна быть равна нулю.
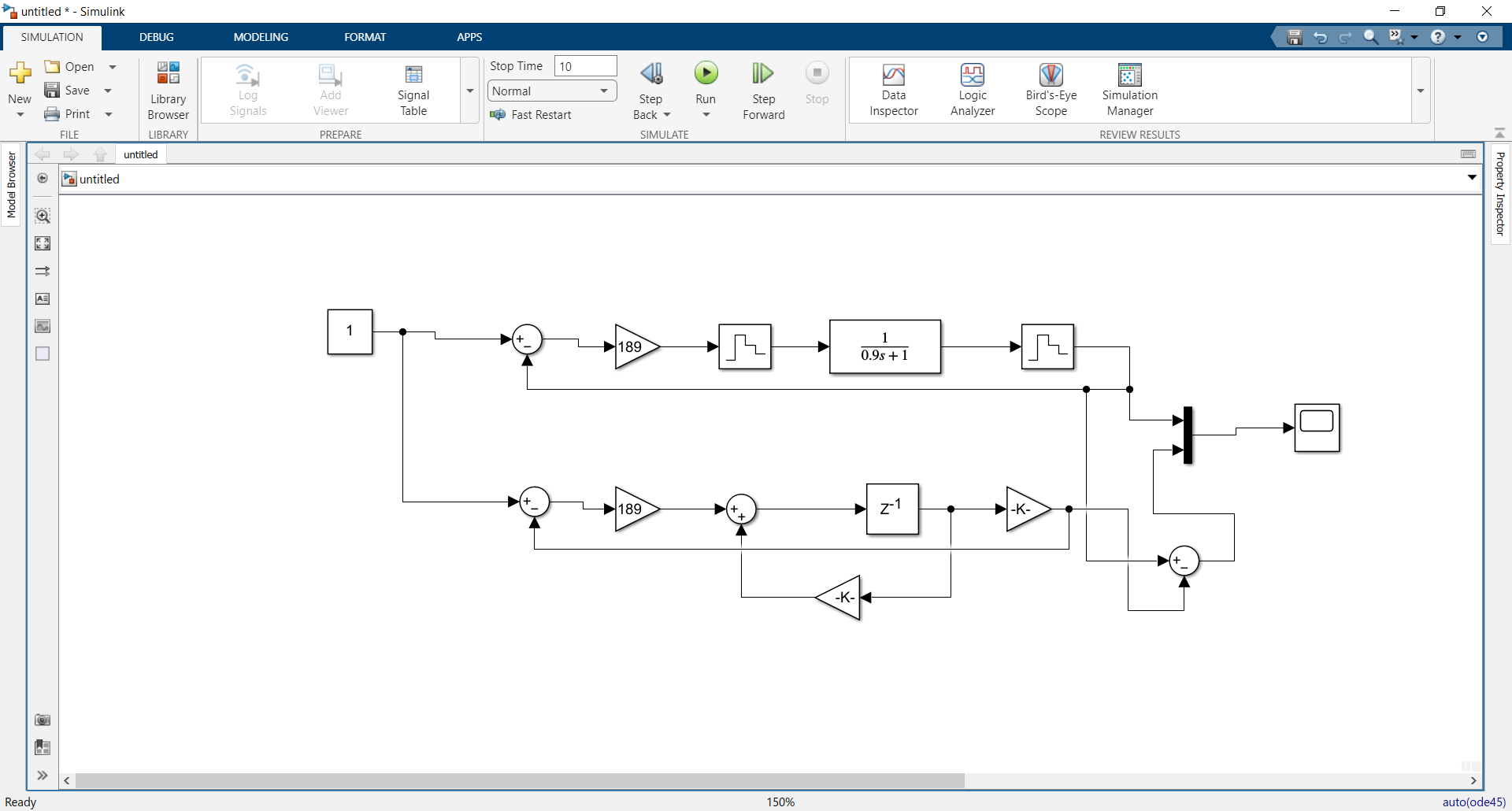
Рисунок 1 - Схема исследования замкнутой цифровой системы.
В настройках симуляции установлено: Solver options: Fixed-step; Solver: ode4(Runge-Kutta); Addition options: Fixed-step size: 0.01.
Выполнено исследование областей устойчивости/неустойчивости дискретной системы. Для этого, устанавливая последовательно значения периода квантования h равными: 8Т, 4Т, 2Т, Т, 0.1, 0.05 и 0.01 нужно вычислить граничные значения коэффициента регулятора К по приближенному (Эйлер) и точному выражениям. Проверим правильность вычисления точного значения К методом моделирования. Значение периода квантования нужно устанавливать в обоих блоках Zero-OrderHold , а также в блоке Delay.
При h=8T граничное значение коэффициента регулятора Кгр=-0,73
При h=4T граничное значение коэффициента регулятора Кгр=-0,47
При h=2T граничное значение коэффициента регулятора Кгр=0,05
При h=T граничное значение коэффициента регулятора Кгр=1,1
При h=0,1 граничное значение коэффициента регулятора Кгр=18
При h=0,05 граничное значение коэффициента регулятора Кгр=37
При h=0,01 граничное значение коэффициента регулятора Кгр=189
На плоскости двух параметров h – Kпостроить область устойчивости, исследуемой линейной дискретной системы.
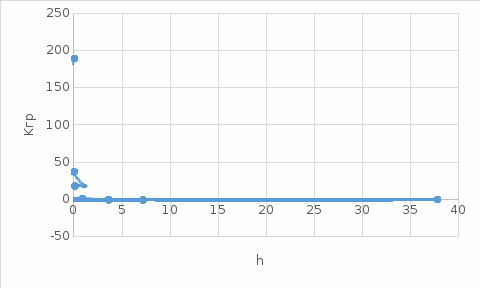
Рисунок 2 – Область устойчивости, исследуемой линейной дискретной системы двух параметров h – K.
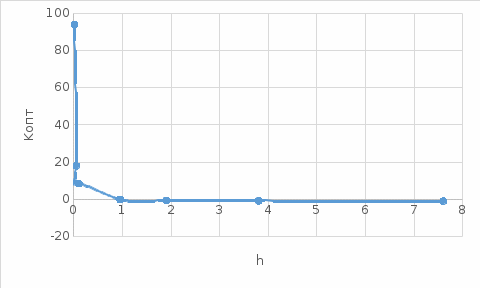
Рисунок 3 – Область устойчивости, исследуемой линейной дискретной системы двух параметров h – Kопт
Для значения параметра h=0.5Tпо формулам для корня характеристического полинома (точной и приближенной) вычислим значения коэффициента регулятора, обеспечивающего в замкнутой системе нулевой корень.
Таким образом, используя схему на (Рисунок 1), произведено моделирование переходных процессов в исследуемой дискретной системе с вычисленными настройками регулятора.
Рисунок 3 – Переходные процессы в исследуемой дискретной системе.
Вывод
В ходе проведения работы были произведены исследования устойчивости замкнутой цифровой системы и расчета цифровой системы с конечной длительностью переходных процессов.
Для приближённого выражения дискретной системы получена аналитическая зависимость коэффициента передачи К регулятора от параметров передаточной функции и периода квантования h системы:
Для точного аналога дискретной системы получена аналитическая зависимость коэффициента передачи К регулятора от параметров передаточной функции и периода квантования h системы:
Для исследуемой линейной дискретной системы построена область устойчивости на плоскости двух параметров h – K, изображённая на (Рисунок 2), при значениях периода квантования h равными: 8Т, 4Т, 2Т, Т, 0.1, 0.05; 0.01 и соответствующих им граничных значений коэффициента регулятора Кгр.