Файл: Литература 7 Задание а) Найти все возможные разложения функции f ( z ) в ряд Лорана (ряд Тейлора) по степеням zz.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Задание 3
Литература 7
Заданиеа) Найти все возможные разложения функции f(z) в ряд Лорана (ряд Тейлора) по степеням z–z0. Указать области, в которых справедливы полученные разложения.б) Используя разложение функции f(z) в ряд Лорана в окрестности точки z=, определить тип особой точки z= и найти вычет функции в этой точке.в) Определить, является ли точка z0 изолированной особой точкой функции f(z). Если да, то, используя разложение функции f(z) в ряд Лорана в окрестности точки z0, определить тип особой точки z0 и найти вычет функции f(z) в этой точке. 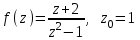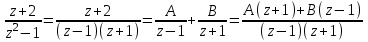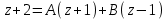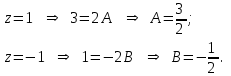.Решениеа) Разложим заданную дробь на сумму простейших: .Отсюда .Придаем переменной z различные значения, получим:Таким образом, 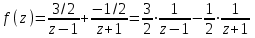. (1)У нас z0=1; функция f(z) теряет аналитичность в точке z0 и в точке z1=-1, отстоящей от z0 на расстоянии 2, поэтому имеем два кольца (рис.1): 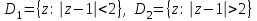. z1 z0Рис.1Первая дробь уже разложена по степеням z–1, поэтому рассматриваем только вторую дробь 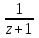.Далее будем пользоваться формулой 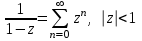. (2)Если 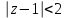, то используя формулу (2), получим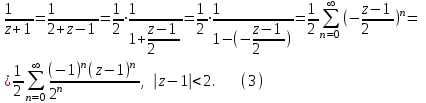Если 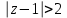, то преобразуя дробь к виду, где можно применить формулу суммы геометрической прогрессии (2), имеем
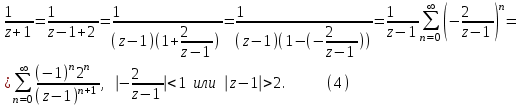
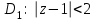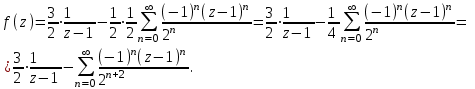
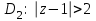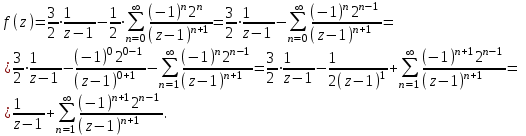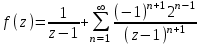
В области разложение функции f(z) в ряд Лорана в силу формул (1) и (3) имеет вид:Этот ряд содержит как положительные, так и отрицательные степени z–1. В области разложение функции f(z) в ряд Лорана в силу формул (1) и (4) имеет вид: Этот ряд содержит только отрицательные степени z–1. б) Разложение функции f(z) в ряд Лорана в окрестности точки z= получено нами в пункте а):Так как главная часть ряда Лорана в окрестности бесконечной точки не содержит бесконечное число членов, то точка z= является устранимой особой точкой.Как известно, вычет функции в изолированной особой точке равен коэффициенту при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 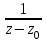для , и этому коэффициенту, взятому с противоположным знаком, для .Тогда .в) Точка z0=1 является изолированной особой точкой, поскольку .Используя ее разложение в ряд Лорана ,делаем вывод, что оно содержит 1 член главной части, поэтому точка является простым полюсом и вычет в ней равен .Ответ: а) В области : ;в области
Задание 3
Литература 7
В области разложение функции f(z) в ряд Лорана в силу формул (1) и (3) имеет вид:Этот ряд содержит как положительные, так и отрицательные степени z–1. В области разложение функции f(z) в ряд Лорана в силу формул (1) и (4) имеет вид: Этот ряд содержит только отрицательные степени z–1. б) Разложение функции f(z) в ряд Лорана в окрестности точки z= получено нами в пункте а):Так как главная часть ряда Лорана в окрестности бесконечной точки не содержит бесконечное число членов, то точка z= является устранимой особой точкой.Как известно, вычет функции в изолированной особой точке равен коэффициенту при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при для 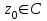, и этому коэффициенту, взятому с противоположным знаком, для 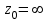.Тогда 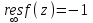.в) Точка z0=1 является изолированной особой точкой, поскольку 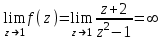.Используя ее разложение в ряд Лорана 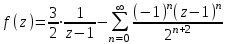,делаем вывод, что оно содержит 1 член главной части, поэтому точка является простым полюсом и вычет в ней равен 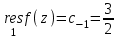.Ответ: а) В области 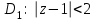: 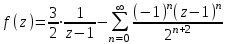;в области
: 
;
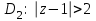
б) z= – устранимая особая точка; 
;
в) z0=1 – простой полюс; 
.
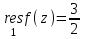Литература
-
Араманович И.Г., Лунц Г.Л., Эльсгольц Л.Э. Функция комплексного переменного. Операционное исчисление. Теория устойчивости.–М.: Наука, 1968.– 415 с. -
Багров В.Г., Белов В.В., Задорожный В.Н., Трифонов А.Ю. Методы математической физики.–Томск: Изд-во НТЛ, 2002.– 672 с. -
Высшая математика. Том 3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. Учеб. для вузов: В 3 т. / Я. С. Бугров, С. М. Никольский; Под ред. В. А. Садовничего. — 6-е изд., стереотип. — М.: Дрофа, 2004.– 512 с. -
Киркинский А.С. Дифференциальные уравнения. Функции комплексной переменной: Учебное пособие.–Алт.гос.техн.ун-т им.И.И.Ползунова. – Барнаул, 2010.– 239 с. -
Краснов М.Л., Киселев А.И., Макаренко Г.И. Операционное исчисление. Теория устойчивости: Задачи и примеры с подробными решениями. Учебное пособие. Изд. 3-е, испр. и доп. - М.: Едиториал УРСС, 2003.–176 с. -
Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного переменного: Задачи и примеры с подробными решениями. Учебное пособие. Изд. 3-е, испр. - М.: Едиториал УРСС, 2003. – 208 с. -
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного.— Изд. 5-е, испр. — М.: Наука, 1987. — 688 с. -
Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной: Учеб.: Для вузов.– 6-е изд., стереот.–М.: ФИЗМАТЛИТ, 2010.– 336 с. -
Чудесенко, В. Ф. Сборник заданий по специальным курсам высшей математике: типовые расчеты : учебное пособие / В. Ф. Чудесенко. - 4-е изд., стер. - СПб. : Лань, 2007. - 192 с. -
Вентцель Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные приложения. - М.: Наука, 1988. - 416 с. -
Вентцель Е.С. Теория вероятностей и математическая статистика: – Учебник. - 5-е изд., стереотип. - М.: Высш. шк., 1999. - 576 с. -
Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с. -
Герасимович А.И. Математическая статистика. – Мн.: Выш. шк., 1983. - 279с. -
Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высш. шк., 1977. – 479 с. -
Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: - Учеб. пособие. 5-е изд. - М.: Высш. шк., 1999. – 276 с.