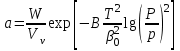ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 29
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3.1. Химическое и фазовые равновесия
Химические реакции сопровождаются превращением одних веществ в другие, отличающиеся от исходных по химическому составу и свойствам. Они делятся на гомогенные и гетерогенные. Гомогенные реакции протекают в пределах одной фазы. Химические реакции, протекающие с участием двух или более фаз, называются гетерогенными.
Химические реакции делятся на необратимые и обратимые. Химические реакции, как правило, обратимы: наряду с прямой реакцией протекает и реакция в обратном направлении. В момент времени, когда скорости прямой и обратной реакций становятся равными, наступает состояние химического равновесия. Условием равновесия любой химической реакции при постоянных температуре и давлении является соблюдение равенств:
dG=0; ∑idni=0, (3.1.1)
где dG – изменение энергии Гиббса; i – химические потенциалы участвующих в реакции веществ; dni – изменение молярных количеств участвующих в реакции веществ.
Количественной характеристикой химического равновесия служит величина, называемая константой равновесия.
В общем случае обратимой реакции
1А1 + 2А2 + …+ iАi = 1B1 + 2B2 + …+ iBi (3.1.2)
при условии термодинамического равновесия концентрации всех реагирующих веществ, согласно закону действующих масс, связаны соотношением:
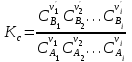, (3.1.3)где Кс – концентрационная константа равновесия;
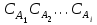и 
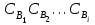– концентрация реагентов, ν1, ν2, … νi и ν1', ν2', … νi' – стехиометрические коэффициенты.Константу равновесия можно выразить также через отношение мольных долей или через их количество.
При анализе реакций, протекающих в газовой фазе, константу равновесия выражают через парциальные давления:
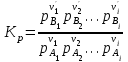. (3.1.4)Для реальных систем закон действующих масс (3.1.3) выполняется строго, если концентрации заменяются термодинамическими активностями, а парциальные давления – летучестями соответствующих веществ:
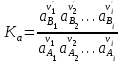, (3.1.5)
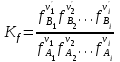. (3.1.6)Равновесие системы может смещаться при изменении концентрации реагирующих веществ, температуры и давления (для газовых реакций). Качественно зависимость химического равновесия от внешних условий описывается принципом Ле Шателье-Брауна: если на систему, находящуюся в термодинамическом равновесии, воздействовать извне, изменяя какой–либо из параметров, то в системе усилится то из направлений процесса, которое ослабляет влияние произведенного воздействия. Например, повышение температуры системы нагреванием стимулирует тот из процессов (прямой или обратный), который протекает с поглощением теплоты. Повышение давления стимулирует тот из процессов, который приводит к уменьшению объема.
Химические реакции протекают самопроизвольно при постоянных давлении и температуре в направлении уменьшения энергии Гиббса. Вычислить изменение энергии Гиббса, а также предсказать направление протекания реакции при заданных условиях, если известны относительные парциальные давления реагирующих веществ в момент их смешения и стандартная константа равновесия можно по уравнению изотермы реакции:
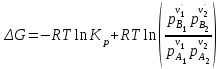. (3.1.7)В стандартном состоянии при всех парциальных давлениях, равных 1 ата, уравнение (3.1.7) запишется в виде:
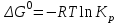. (3.1.8)В случае отсутствия табличных значений
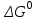их рассчитывают, используя уравнение:
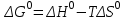, (3.1.9)где
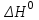и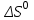 
– стандартные изменения энтальпии и энтропии реакции.На рис. 3.1 приведен пример вычисления константы равновесия реакции:
NH3 + HCl = NH4Cl. (3.1.10)
Рис. 3.1. Вычисление константы равновесия реакции
В случае химической реакции, протекающей при постоянных температуре и давлении, изменение энтальпии равно взятому с обратным знаком тепловому эффекту реакции.
На рис. 3.2 приведен пример вычисления теплового эффекта реакции, выполненный в системе Маthcad.
В отличие от химического равновесия при фазовом равновесии химического взаимодействия между веществами не происходит, а протекают лишь процессы перехода веществ из одной фазы в другую. Фазовые переходы бывают следующего типа: т1↔т2, т↔ж, т↔г, ж1↔ж2, ж↔г.
Рис. 3.2. Вычисление теплового эффекта реакции
Условием фазового равновесия является соблюдение при постоянных температуре и давлении равенств:
dG=0; ∑idni=0, (3.1.11)
где i – химический потенциал i-го компонента системы; ni – число молей i-го компонента.
В гетерогенной системе при Р=cоnst и Т=cоnst равновесие характеризуется равенством химических потенциалов каждого компонента во всех фазах:
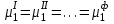, (3.1.12)где
,
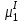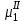– химический потенциал i-го компонента в первой и второй фазах, Ф – число фаз.На равновесие химико-технологической системы обычно оказывают влияние температура, давление и концентрация. Число независимых параметров, которое можно произвольно изменять без нарушения равновесия системы, может быть найдено по правилу фаз:
Ф + S = К + 2, (3.1.13)
где S – число степеней свободы; К – число компонентов системы.
Связь между давлением, объемом и температурой физически однородной системы в состоянии термодинамического равновесия определяется уравнением состояния:
f(P,V,T) = 0. (3.1.14)
Примером уравнения состояния идеального газа служит уравнение Клайперона:
РV =nRT, (3.1.15)
где R – универсальная газовая постоянная; Р и V – давление и объем газа; n – число молей идеального газа; Т – абсолютная температура.
Одно из первых уравнений состояния реального газа − уравнение Ван-дер-Ваальса:
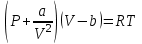, (3.1.16)где а и b – постоянные, зависящие от природы газа, учитывающие влияние сил притяжения между молекулами и конечность их объема.
Для жидкостей из-за сложности учета всех особенностей взаимодействия молекул пока не удается теоретически получить общее уравнение состояния.
Для получения уравнения состояния твердых тел используют теорию колебаний кристаллической решетки. Однако до сих пор не существует универсального уравнения состояния твердых тел.
В соответствии с уравнением (3.1.14) экспериментальные данные давления, объема и температуры для равновесной системы должны быть представлены в виде пространственной координаты. Подобные диаграммы мало удобны для практического применения. Для характеристики состояния однокомпонентной системы чаще используют плоскую фазовую диаграмму, представляющую собой проекцию пространственной диаграммы состояния на плоскость Р-Т. На рис. 3.3. в качестве примера приведена плоская диаграмма состояния воды.
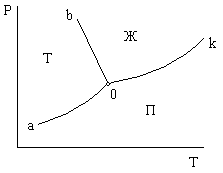
Рис. 3.3. Диаграмма состояния воды
На диаграмме (рис. 3.3) видно три поля однофазного состояния: жидкого (ж), парообразного (п) и твердого (т). Линии соответствуют двухфазному состоянию системы: 0а – линия возгонки, 0b – линия плавления, 0k – линия испарения. В точке 0 с координатами Р=610,48 Па и Т=273,16 К в равновесии находятся три фазы. В этой точке система безвариантна. Таким же свойством обладает и критическая точка k: Р=221,406∙105 Па и Т=647,35 К. Например, в системе Н2О(ж) = Н2О(п) в соответствии с уравнением (3.1.13) имеем: Ф = 1−2+2 =1. Следовательно, каждой температуре отвечает единственное значение давления насыщенного пара. Если изменить только один параметр, например Р (при Т=const) или T (при Р=const), то равновесие нарушается, т.к. исчезнет одна из фаз. Это приведет к увеличению числа степеней свободы на единицу, т.е. создает возможность менять одновременно давление и температуру независимо друг от друга.
Для двухкомпонентной системы, на равновесие в которой из внешних факторов оказывают влияние только давление и температура, правило фаз выражается уравнением:
С = 4 – Ф. (3.1.17)
Уравнение состояния для двухкомпонентной системы должно содержать в отличие от уравнения (3.1.14) число молей компонентов n1 и n2 :
f(P,V,T,n1,n2) = 0. (3.1.18)
Гомогенные области двухкомпонентных систем представляют собой растворы. Растворы по физическому состоянию могут быть газообразные, жидкие и твердые. В химической технологии наиболее часто встречаются следующие виды растворов: растворы газов в жидкостях; растворы газов в твердых телах; растворы, образованные двумя жидкостями и др.
Межфазное равновесие для идеальных растворов описывается законом Генри:
р* = Ех, (3.1.19)
где р* – парциальное давление компонента в газовой фазе над равновесной с газом жидкостью; Е – константа Генри; х – мольная доля компонента в жидкости.
Числовые значения Е зависят от температуры и природы жидкости.
Идеальные растворы подчиняются закону Рауля:
р* = Рх, (3.1.20)
где р* – парциальное давление компонента в парогазовой смеси над жидкостью в равновесных условиях; Р – давление насыщенного пара чистого компонента, Р=f(Т).
Влияние растворенных веществ на растворимость газа в системе газ–жидкость учитывается в эмпирическом уравнении Сеченова И.М.:
lnx = lnx0 – kC, (3.1.21)
где х, х0 – растворимость газа в растворе и чистом растворителе; С – концентрация раствора; k – эмпирический коэффициент.
В системе газ–твердое тело количество адсорбированного вещества зависит от концентрации адсорбтива и температуры. В общем виде эта зависимость имеет вид:
а = f(С,Т). (3.1.22)
При постоянном значении температуры системы зависимость (3.1.22) упрощается:
а = f(С) при Т=const. (3.1.23)
Концентрация поглощаемого вещества может быть заменена его парциальным давлением в парогазовой смеси. Тогда имеем:
а = f(р) при Т=const. (3.1.24)
Приведем наиболее используемые для практических расчетов процесса адсорбции уравнения изотерм.
Мономолекулярная адсорбция на однородных поверхностях из газовой фазы описывается уравнением Ленгмюра:
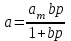, (3.1.25)где аm – предельное значение адсорбции; b – адсорбционный коэффициент.
Для описания адсорбции на неоднородных поверхностях используется эмпирическое уравнение Фрейндлиха:
a = kpn, (3.1.26)
где k и n – константы.
Для полимолекулярной адсорбции паров на твердых поверхностях используется уравнение Бранауера-Эммета-Теллера (уравнение БЭТ):
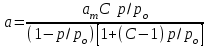, (3.1.27)где ро – давление насыщенного пара при температуре адсорбции; С – константа.
Дубининым М.М. разработана теория объемного заполнения микропор и получено следующее уравнение изотеры адсорбции:
