Добавлен: 09.11.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача. Ориентированный граф задан связями между его вершинами (например, A B означает наличие дуги из вершины А в вершину B). Нарисовать этот граф, представить его в виде матрицы смежности, вывести степень вершины каждого графа, а также полустепени захода и исхода для каждой вершины, проверить граф на наличие в нем Эйлерова пути, для заданной вершины выполнить обход графа в ширину и в глубину.
10. Граф
A B B C A E E B B F C D D H H G F C G F F E
Начальная вершина обхода C.
По условию задачи нам дан ориентированный граф. Выполним его чертёж, отмечая стрелками направления входа и захода в вершины графа.
Н
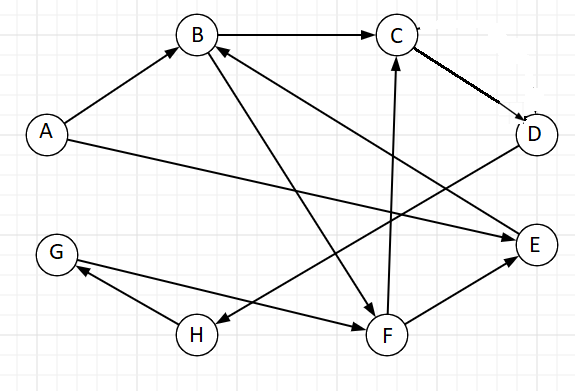
а основании этого строим матрицу смежности, ставя единицу там, где есть связь между вершинами в соответствии столбец – строка.
Искомая матрица смежности задаётся в виде таблицы:
| | A | B | C | D | E | F | H | G |
| A | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| B | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| E | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Множество вершин графа (их – 8):
V = A, B, C, D, E, F, G , H, V = 8
Множество рёбер графа (их – 11):
E = A B; B C; A E; E B; B F; C D; D H; H G; F C; G F; F E = 9
Найдём полустепени исхода и захода вершин:
d - A =1; d + A = 2; d - B = 2; d + B = 2; d – C = 1; d + C = 2; d – D = 1; d + D = 1; d - E = 2; d + E = 1; d – H = 1; d + H = 1; d – F = 2; d + F = 2;
Следовательно, степени вершин равны:
dA = 3, dE = 1, dB = 4, dG = 1, dC = 3, dH = 2, dD = 2, dF = 4;
Сумма степеней вершин графа: 3 + 1 + 4 + 1 + 3 + 2 + 2 + 4 = 18 = 2∙E = 2∙9
В графе нет эйлерового пути, так как при обходе из вершины A выпадает ребро А,Е.
Обход в глубину
Пусть вершина C является начальной вершиной обхода (красим её в серый цвет).
Таким образом, включаем вершину C в список обработанных вершин.
Так как граф – ориентированный, то окрашиваем в серый цвет достижимую из точки C вершину D.
Далее идём в вершину H, окрашиваем её . Следовательно, пройдены три вершины.
Дальше мы проходим вершину G, окрасив её. Попав в вершину G и окрасив её, мы проходим в вершину F. Затем идем в вершину Е, затем в вершину В. Завершаем обход с результатом (С; D; H; G; F; E; B)
Обход в ширину
-
пусть стартовая вершина – С -
включаем С в список обработанных вершин: список = (С) -
помещаем в очередь смежные с С вершины, т.е. D: очередь = (D) -
извлекаем из очереди вершину D? т.к. она не обработана, добавляем ее в список: список = (C, D) -
смежные с D вершины – это H, помещаем в очередь вершину H: очередь = (Н) -
извлекаем из очереди вершину Н, т.к. Н не обработана, помещаем ее в список: список = (С, D, H) -
смежные с H вершины – это G; помещаем в очередь вершину G: очередь = (G) -
извлекаем из очереди вершину G, т.к. G не обработана, помещаем ее в список: список = (С, D, H, G) -
смежные с G вершины – это F; помещаем в очередь вершину F: очередь = (F) -
извлекаем из очереди вершину F, т.к. F не обработана, помещаем ее в список: список = (С, D, H, G, F) -
смежные с F вершины – это E и C; С – обработана, помещаем в очередь вершину Е: очередь = (Е) -
извлекаем из очереди вершину Е, т.к. Е не обработана, помещаем ее в список: список = (С, D, H, G, F, Е) -
смежные с Е вершины – это В; помещаем в очередь вершину В: очередь = (В) -
извлекаем из очереди вершину В, т.к. В не обработана, помещаем ее в список: список = (С, D, H, G, F, Е, В) -
Смежные с В вершины С и F, т.к. они уже обработаны очередь становится пустой, то поиск заканчивается с результатом (С, D, H, G, F, Е, В)