ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 12
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Уфимский государственный авиационный технический университет
Факультет авионики, энергетики и инфокоммуникаций
Кафедра телекоммуникационных систем
Расчетно-графическая работа
по дисциплине
| Подп. и дата | |
| Подп. и дата | |
| Взаим. инв. № | |
| Инв. № подл. | |
| Инв. № дубл. | |
Проектирование цифрового фильтра нижних частот
1202.403208.000 ПЗ
| Группа ИКТ-412 | Фамилия И.О. | Подпись | Дата | Оценка |
| Студентка | Боисланова Д.А. | | | |
| Консультант | Комиссаров А.М. | | | |
| Принял | Комиссаров А.М. | | | |
Уфа 2017
С
 одержание
одержаниеЗадание на расчетно-графическую работу…………………………………....3
Исходные данные………………………………………………………………3
Расчетная часть………………………………………………………………....5
Заключение………………………………………………………………….....18
Расчетная часть………………………………………………………………....5 2
Расчетная часть 5
6.Построим импульсную и переходную характеристики ЦФНЧ: 17
18
Заключение 21
З
 адание на расчетно-графическую работу
адание на расчетно-графическую работу-
определить передаточные функции аналогового прототипа и цифрового фильтра; -
рассчитать их модули и построить графики АЧХ; -
определить разностное уравнение; -
построить импульсную и переходную характеристики.
Исходные данные
Вариант 6
| Данные для проектирования цифрового БИХ-фильтра НЧ (фильтр Баттерворта) | ||||
| Верхняя граница затухания в полосе пропускания, 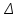 a [дБ] a [дБ] | Нижняя граница затухания в полосе задерживания, a0 [дБ] | Граничная частота полосы пропускания, fг.п [Гц] | Граничная частота полосы задерживания, fг.з [Гц] | Частота дискретизации, fд [Гц] |
| 0,044 | 30 | 1160 | 2840 | 8000 |
Таблица 1 - Исходные данные
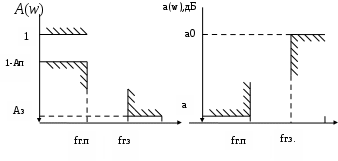
Рисунок 1 - Схемы допусков на амплитудно-частотную характеристику A(w) и характеристику затухания a(w)
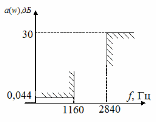

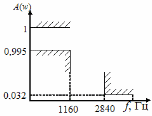
Рисунок 2 - Схемы допусков на амплитудно-частотную характеристику A(w) и характеристику затухания a(w) для данного варианта
АЧХ A(w) и характеристика затухания a(w) связаны между собой соотношением:
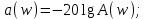
Связь между параметрами Aп иa, а также Aз иa0можно установить, используя:
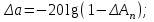
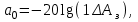
Отсюда получим:
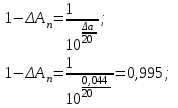
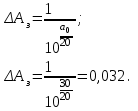
Р
 асчетная часть
асчетная часть-
Расчет нормированных «цифровых» граничных частот:
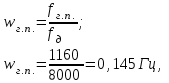
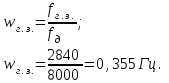
-
Расчет параметра преобразования:
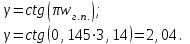
-
Нахождение граничной «аналоговой» частоты Ωk полосы задерживания АФ-прототипа:
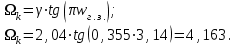
-
Определение передаточной функции T(s) аналогового нормированного фильтра-прототипа нижних частот типа B.
4.1. Определение модуля коэффициента отражения |p| по заданной
величине ∆а = 0,044 дБ (из таблицы П.1.1 стр.241 учебника Л. М. Гольденберга «ЦОС»):
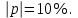
4.2. Определение вспомогательного параметра L с помощью величин
а0 = 30 дБ и |p| = 10% по общей номограмме (по рисунку П.1.1 стр.241 учебника Л. М. Гольденберга «ЦОС»):
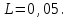
4
 .3. Определение порядка n передаточной функции с помощью
.3. Определение порядка n передаточной функции с помощьюзаданной величины Ωk = 4,163 и полученной величины L= 0,05 (по рисунку П.1.2 стр.242 учебника Л. М. Гольденберга «ЦОС»):
n = 4.
4.4. Записываем передаточную функциюT(s) фильтра в общем виде:
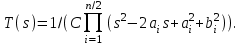
4.5. Определяем численные значения коэффициентов передаточной
функции T(s) (из таблицы П.1.2 стр.241 учебника Л. М. Гольденберга «ЦОС»):
С = 0,10050378;
а1 = 0,6796636758;
а2 = 1,6408532639;
±b1 = 1,6408532638;
±b2 = 0,6796636757.
4.6. Записываем передаточную функцию T(s) аналогового нормирован-
ного ФНЧ с численными значениями коэффициентов:
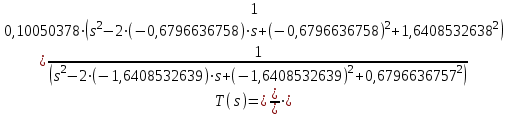
Проведем расчет в программе Maple 13 с использованием следующих подстановок:
s= j;
Расчет АЧХ:
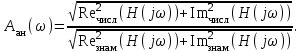


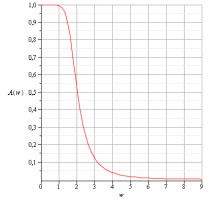
Рисунок 3 - АЧХ аналогового прототипа
-
О пределим передаточную функцию H(z) цифрового ФНЧ
пределим передаточную функцию H(z) цифрового ФНЧ
с помощью билинейного преобразования.
Проведем расчет в программе Maple 13 с использованием следующих подстановок:
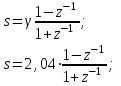
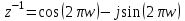 .
.






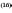










Рисунок 4 - АЧХ цифрового фильтра Баттерворта
Проверим:
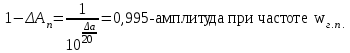 ;
;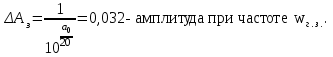
-
П
 остроим импульсную и переходную характеристики ЦФНЧ:
остроим импульсную и переходную характеристики ЦФНЧ:
Передаточная функция цифрового фильтра:
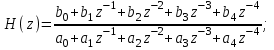
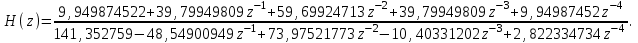
Значит, коэффициенты разностного уравнения будут равны:
b0 =
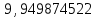 ;
;b1 =
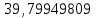 ;
;b2 =
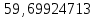 ;
;b3 =
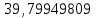 ;
;b4 =
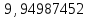 ;
;a0 =
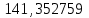 ;
;a1 =
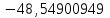 ;
;a2 =
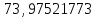 ;
;a3 =
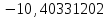 ;
;a4 =
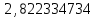 .
.Перейдем к разностному уравнению вида:
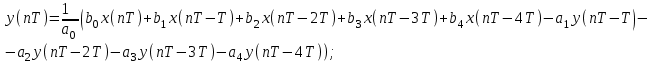
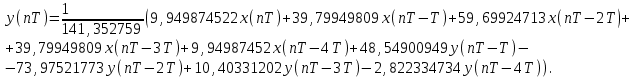
а) Импульсная характеристика
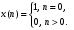
Д
 ля построения импульсной характеристики ЦФНЧ воспользуемся пакетом Microsoft Excel.
ля построения импульсной характеристики ЦФНЧ воспользуемся пакетом Microsoft Excel.Таблица 2 - Данные в Microsoft Excel для построения импульсной характеристики
| n | x(nT) | y(nT) |
| -4 | 0 | 0 |
| -3 | 0 | 0 |
| -2 | 0 | 0 |
| -1 | 0 | 0 |
| 0 | 1 | 0,07039 |
| 1 | 0 | 0,305738 |
| 2 | 0 | 0,490513 |
| 3 | 0 | 0,29521 |
| 4 | 0 | -0,06382 |
| 5 | 0 | -0,14642 |
| 6 | 0 | -0,00495 |
| 7 | 0 | 0,064333 |
| 8 | 0 | 0,015187 |
| 9 | 0 | -0,02589 |
| 10 | 0 | -0,01201 |
| 11 | 0 | 0,00926 |
| 12 | 0 | 0,007255 |
| 13 | 0 | -0,00272 |
| 14 | 0 | -0,00381 |
| 15 | 0 | 0,000464 |
Строим импульсную характеристику цифрового фильтра
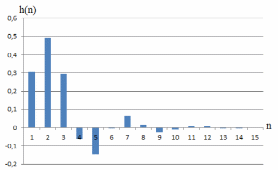
Рисунок 5 - Импульсная характеристика ЦФНЧ
б) Переходная характеристика
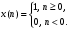
Для построения переходной характеристики ЦФНЧ воспользуемся пакетом Microsoft Excel.
Т
 аблица 3 - Данные в Microsoft Excel для построения переходной характеристики
аблица 3 - Данные в Microsoft Excel для построения переходной характеристики| n | x(nT) | y(nT) |
| -4 | 0 | 0 |
| -3 | 0 | 0 |
| -2 | 0 | 0 |
| -1 | 0 | 0 |
| 0 | 1 | 0,07039 |
| 1 | 1 | 0,376128 |
| 2 | 1 | 0,866641 |
| 3 | 1 | 1,161851 |
| 4 | 1 | 1,098026 |
| 5 | 1 | 0,951607 |
| 6 | 1 | 0,946653 |
| 7 | 1 | 1,010986 |
| 8 | 1 | 1,026173 |
| 9 | 1 | 1,00028 |
| 10 | 1 | 0,988273 |
| 11 | 1 | 0,997533 |
| 12 | 1 | 1,004788 |
| 13 | 1 | 1,002067 |
| 14 | 1 | 0,998257 |
| 15 | 1 | 0,998721 |
| 16 | 1 | 0 |
| 17 | 1 | 0 |
| 18 | 1 | 0 |
| 19 | 1 | 0 |
| 20 | 1 | 0,07039 |
| 21 | 1 | 0,376128 |
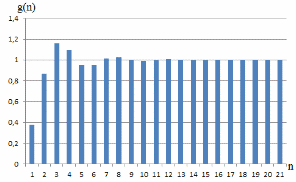
Рисунок 6 - Переходная характеристика ЦФНЧ
Из графика переходной характеристики видно, что при трубке точности 5% время переходного процесса tпер. ≈ 4 с.
З
 аключение
аключениеВ данной расчетно-графической работе был спроектирован цифровой ФНЧ Баттерворта (типа B) 4-го порядка. Для этого была рассчитана передаточная функция аналогового фильтра низкой частоты и построена его АЧХ.
Затем с помощью билинейного преобразования получили передаточную функцию цифрового фильтра, построили его амплитудно-частотную характеристику. Используя разностное уравнение, исследовали импульсную и переходную характеристику полученного ФНЧ.
Спроектированный цифровой БИХ-фильтр полностью удовлетворяет заданным начальным условиям, обеспечивает требуемую полосу пропускания и задержки.