ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 24
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное АВТОНОМНОЕ образовательное учреждение высшего образования «Национальный исследовательский ядерный университет «МИФИ» |
| Волгодонский инженерно-технический институт – филиал федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский ядерный университет «МИФИ» (ВИТИ НИЯУ МИФИ) |
ФАКУЛЬТЕТ _Атомной энергетики и машиностроения__________
КАФЕДРА _Информационных и управляющих систем________
СПЕЦИАЛЬНОСТЬ _Системный анализ и управление _______________
ОТЧЕТ
ПО
ЛАБОРАТОРНОЙ РАБОТЕ
ПО ДИСЦИПЛИНЕ Математические методы системного анализа_________
РАБОТЫ ВЫПОЛНИЛ СТУДЕНТ
Кулинченко Данил Анатольевич, САУ-22-ДМ____________________
фамилия, имя, отчество, группа, подпись
РАБОТЫ ПРИНЯЛ ПРЕПОДАВАТЕЛЬ
Шпицер Владимир Яковлевич, д. т. н., профессор ______________________
фамилия, имя, отчество, ученая степень, ученое звание, должность
Волгодонск
2022 г.
Лабораторная работа №1
Тема работы: «Система, представленная сигналом»
Цель работы: «Исследовать поведение системы, основываясь на выходном сигнале; создать модель, способную к предсказанию поведения системы»
Постановка задачи:
1. Предсказать поведение системы на некотором промежутке времени.
2. Проанализировать свойства сигнала.
Ход работы:
1. Рассмотрим промышленный сигнал, представленный на рисунке 1
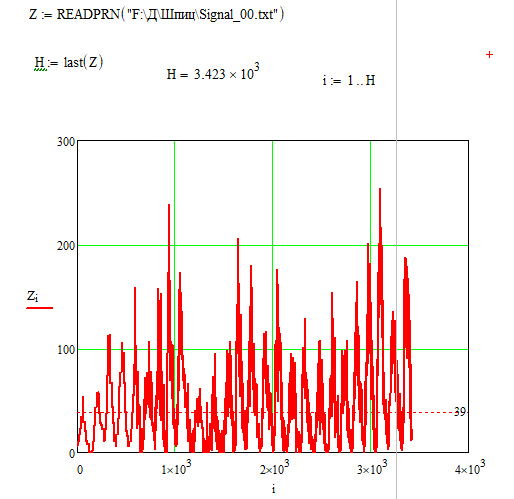
Рисунок 1 – Исходный сигнал
2. Выделим фрагмент сигнала в 300 точек. Таким образом, будем считать, что в данный момент времени известны значения сигнала только в этом промежутке.
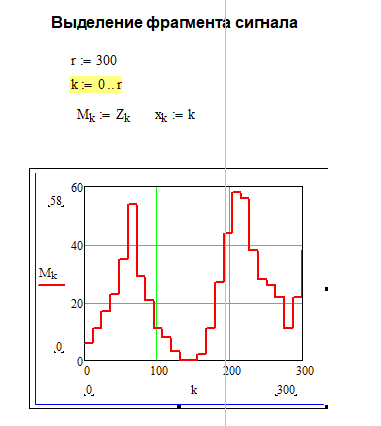
Рисунок 3 – Буфер обрабатываемых значений сигнала
3. Таким образом, для предсказания поведения системы можно применить линейное и полиномиальное предсказание.
Перейдём к построению на основании сглаженной версии сигнала прогностических моделей. Построим линейную регрессию с помощью функции slope, возвращающей коэффициент a линейной регрессии (a*x+b), и функции intercept, возвращающей коэффициент b. Таким образом, найдя точку пересечения полученной линейной модели с заданным предельным уровнем сигнала, можно предсказать момент времени превышения нормативного уровня x = 795.5
Кроме того, предсказать поведение системы можно с помощью квадратичной регрессии. В данном случае были использованы функции regress (возвращает вектор коэффициентов для построения регрессии) и interp (возвращает результат регрессии) и была выбрана вторая степень полинома.
Преимуществом линейной модели является её простота, кроме того, в данном случае точность предсказания, обеспечиваемая линейной моделью, незначительно отличается от точности предсказания, обеспечиваемой полиномиальной моделью.
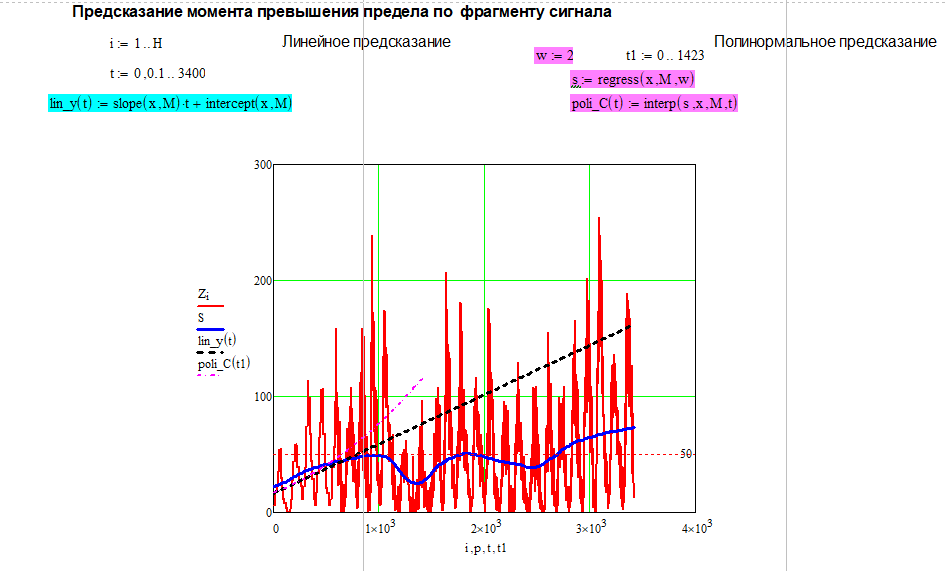
Рисунок 4 – Предсказание поведения системы на основе линейной и полиномиальной моделей
4. Перейдём к исследованию свойств сигнала. Определим степень предсказуемости сигнала на промежутке в 30 точек по известным значениям в 270 точках. Для начала определим предсказуемость мощности исходного сигнала. Видно, что данный сигнал является недетерминированным.
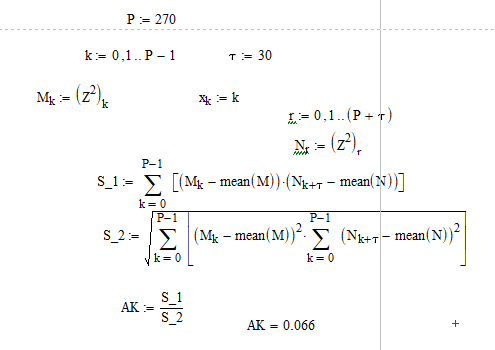
Рисунок 5 – Определение предсказуемости исходного сигнала
5. Теперь определим предсказуемость линейной модели сигнала. Данная модель также является хорошо детерминированной.

Рисунок 6 – Определение предсказуемости линейной модели
6. Теперь определим предсказуемость полиномиальной модели сигнала. Данная модель является более детерминированной, чем линейная.
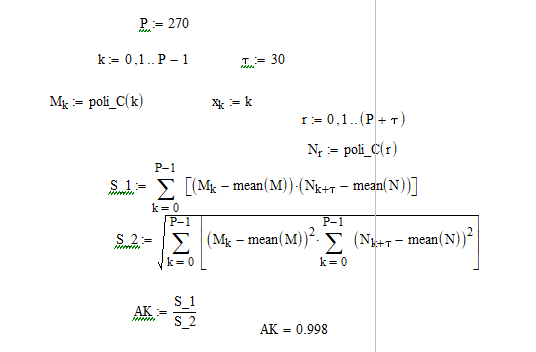
Рисунок 7 – Определение предсказуемости полиномиальной модели
7. Далее исследуем регулярность сигнала и его моделей. Исходный сигнал является шумовым.

Рисунок 8 – Определение регулярности мощности исходного сигнала
8. Определим регулярность линейной и полиномиальной моделей сигнала. Обе модели являются регулярными, однако коэффициент линейной модели меньше коэффициента полиномиальной модели.
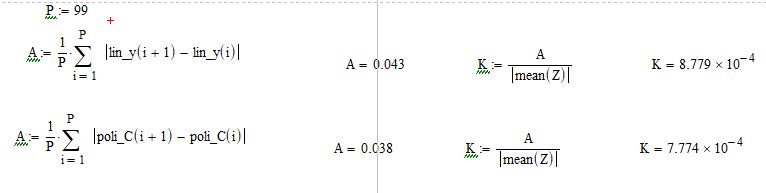
Рисунок 9 – Определение регулярности линейной и полиномиальной моделей
Вывод: В ходе выполнения данной лабораторной работы по данному промышленному сигналу было исследовано поведение системы: были построены линейная и полиномиальная модель.
Было установлено, что применение сплайнов пригодно для интерполяции исходного сигнала, но не пригодно для предсказания поведения системы. Линейная модель отличается простотой и регулярностью, а полиномиальная модель со второй степенью полинома регрессии – хорошей детерминированностью. Однако обе модели являются пригодными для предсказания поведения системы и повышают регулярность и предсказуемость данных о системе.