Файл: Задания по геометрии за 8 класс Работа 1.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 11

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задания по геометрии за 8 класс

Работа №1

  1. Периметр параллелограмма 50 см. Одна из его сторон на 5 см больше другой. Найдите длины сторон параллелограмма.

  2. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4 : 5.

  3. Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон.

  4. В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ, ∠ADB = ∠BDC = 30°. Найдите длину AD, если периметр трапеции 60 см.

  5. * В параллелограмме ABCD биссектрисы углов АВС и BCD пересекаются в точке M1. На прямых АВ и CD взяты точки К и Р так, что А – В – К, D – С – Р. Биссектрисы углов КВС и ВСР пересекаются в точке М2, М1М2 = 8 см. Найдите AD.

Работа №2

  1. Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 30°. Найдите площадь параллелограмма.

  2. Вычислите площадь трапеции ABCD с основаниями AD и ВС, если AD = 24 см, ВС = 16 см, ∠A = 45°, ∠D = 90°.

  3. Дан треугольник АВС. На стороне АС отмечена точка С так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см.

  4. * Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон.

Работа №3

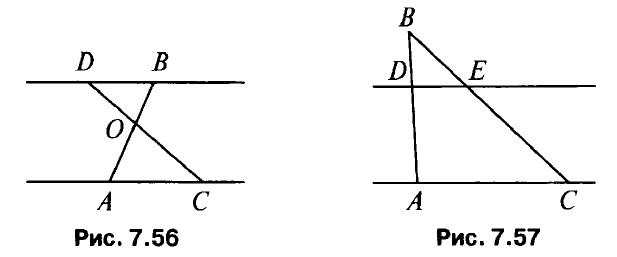
  1. Дано: АО = 6,8 см, СО = 8,4 см, ОВ = 5,1 см, OD = 6,3 см (рис. 7.56).
    Доказать: АС||BD. Найти: a) DB : АС, б) PAOC : PDBO, в) SDBO : SAOC.

  2. Диагонали ромба ABCD пересекаются в точке О, BD = 16 см. На стороне АВ взята точка К так, что ОК ⊥ АВ и ОК = 4√3 см. Найдите сторону ромба и вторую диагональ.

  3. В выпуклом четырехугольнике ABCD АВ = 9 см, ВС = 8 см, CD = 16 см, AD = 6 см, BD = 12 см. Докажите, что ABCD — трапеция.

  4. * В равнобедренном треугольнике MNK с основанием МК, равным 10 см, MN = NK = 20 см. На стороне NK лежит точка А так, что AК : AN =1 : 3. Найдите AM.



Работа №4

  1. На стороне ВС треугольника АВС выбрана точка D так, что BD : DC = 3 : 2, точка К — середина отрезка АВ, точка F — середина отрезка AD, КF = 6 см, ∠ADC = 100°. Найдите ВС и ∠AFK.

  2. В прямоугольном треугольнике ABC ∠C = 90°, АС = 4 см, СВ = 4√3 см, СМ — медиана. Найдите угол ВСМ.

  3. В равнобедренной трапеции основания равны 8 см и 12 см, меньший угол равен α. Найдите периметр и площадь трапеции.

  4. В равнобедренном треугольнике АВС с основанием АС медианы пересекаются в точке О. Найдите площадь треугольника АВС, если ОА = 13 см, ОВ = 10 см.

  5. * В трапеции ABCD (ВС||AD) АВ ⊥ BD, BD = 2√5, AD = 2√10, СЕ — высота треугольника BCD, a tg∠ECD = 3. Найдите BE.

Работа №5

  1. В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см, 4 см, 5 см. Определите вид треугольника.

  2. Точки А и В делят окружность с центром О на дуги AMВ и АСВ так, что дуга АСВ на 60° меньше дуги AMВ. AM — диаметр окружности. Найдите углы АМВ, АВМ, АСВ.

  3. Хорды АВ и CD пересекаются в точке Е так, что АЕ = 3 см, BE = 36 см, СЕ : DE = 3 : 4. Найдите CD и наименьшее значение радиуса этой окружности.

  4. * В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию, — 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника.

Итоговая работа №6

  1. Боковая сторона равнобедренного треугольника равна 10 см, а его основание 12 см. Найдите его площадь.

  2. Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК и КС, равные соответственно 8 см и 4 см. Найдите периметр параллелограмма.

  3. В трапеции ABCD углы А и В прямые. Диагональ АС — биссектриса угла А и равна 6 см. Найдите площадь трапеции, если угол CDA равен 60°.

  4. В окружности проведены две хорды АВ и CD, пересекающиеся в точке К, КС = 6 см, АК = 8 см, ВК + DK = 28 см. Найдите длины ВК и DK.

  5. Квадрат со стороной 8 см описан около окружности. Найдите площадь прямоугольного треугольника с острым углом 30°, вписанного в данную окружность.

Смотрите также файлы