Файл: Идентификация законов распределения случайных величин.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 9
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский государственный технический университет им. Н. Э. Баумана
(национальный исследовательский университет)»
(МГТУ им. Н. Э. Баумана)

ИДЕНТИФИКАЦИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНЫХ ВЕЛИЧИН
Домашнее задание № 1 по курсу
«Метрология, стандартизация и сертификация»
Вариант - 4
Москва, 2023
Исходные данные
Результаты измерения сопротивлений резисторов номиналом 20 кОм в составе партии из 260 шт. сведены в статистический ряд. Идентифицировать закон распределения результатов измерений. Исходные данные ряда представлены в таблице 1.
Таблица 1 – Исходные данные
| Ri | 19,85;19,92 | 19,92;19,99 | 19,99;20,06 | 20,06;20,13 | 20,13;20,20 | 20,20;20,27 | 20,27;20,34 | 20,34;20,41 |
| ni | 6 | 9 | 33 | 71 | 79 | 41 | 16 | 5 |
Расчет
-
Найдем статистические частоты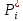 по формуле (1):
по формуле (1):
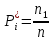 n = 260 | (1) |
Полученные значения представлены в таблице 2.
Таблица 2 – Статистический ряд
| Ri | 19,85;19,92 | 19,92;19,99 | 19,99;20,06 | 20,06;20,13 | 20,13;20,20 | 20,20;20,27 | 20,27;20,34 | 20,34;20,41 |
| ni | 6 | 9 | 33 | 71 | 79 | 41 | 16 | 5 |
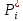 | 0,023 | 0,035 | 0,127 | 0,273 | 0,304 | 0,158 | 0,061 | 0,019 |
-
Построим гистограмму как графическое представление статистической плотности распределения. Вид гистограммы на рис. 1 свидетельствует о том, что возможной теоретической моделью данного распределения является нормальный закон, который и примем с целью идентификации. -
Определим статистические оценки числовых параметров нормального распределения — математического ожидания ???? и дисперсии ????.
Среднее арифметическое значение погрешности m* найдем по формуле (2):
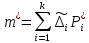 где 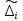 – среднее арифметическое погрешности – среднее арифметическое погрешности 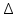 в i-м разряде (интервале). в i-м разряде (интервале).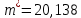 угл.с угл.с | (2) |
Статистическое СКО S найдем с помощью формулы (3):
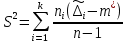 | (3) |
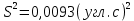
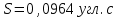
-
Найдем теоретические вероятности попадания случайной величины в каждый из интервалов, используя формулу (4) и таблицу функции Лапласа.
Теоретическая вероятность в интервале (xi, xi+1) при нормальном законе распределения:
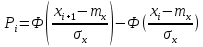 | (4) |
Таблица 3 – Результаты расчетов теоретических вероятностей
| i | ni | xi, xi+1 |  | 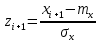 | Ф(zi) | Ф(zi+1) | Pi |
| 1 | 6 | 19,85;19,92 | -2,99 | -2,26 | -0,49859 | -0,48813 | 0,01045 |
| 2 | 9 | 19,92;19,99 | -2,26 | -1,54 | -0,48813 | -0,43767 | 0,05045 |
| 3 | 33 | 19,99;20,06 | -1,54 | -0,81 | -0,43767 | -0,29092 | 0,14674 |
| 4 | 71 | 20,06;20,13 | -0,81 | -0,084 | -0,29092 | -0,03337 | 0,25755 |
| 5 | 79 | 20,13;20,20 | -0,084 | 0,64 | -0,03337 | 0,2396 | 0,27298 |
| 6 | 41 | 20,20;20,27 | 0,64 | 1,37 | 0,23960 | 0,41434 | 0,17474 |
| 7 | 16 | 20,27;20,34 | 1,37 | 2,09 | 0,41434 | 0,48186 | 0,06751 |
| 8 | 5 | 20,34;20,41 | 2,09 | 2,82- | 0,48186 | 0,49759 | 0,01573 |
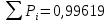 | |||||||
В рассматриваемом примере
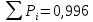 , так как табличные аргументы функции Лапласа обычно позволяют учесть только два разряда после запятой.
, так как табличные аргументы функции Лапласа обычно позволяют учесть только два разряда после запятой.-
Определим меру расхождения между теоретическими вероятностями и статистическими частотами.
В качестве меры расхождения между теоретическими вероятностями и статистическими частотами на практике используется критерий 2 Пирсона («хи-квадрат»):
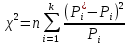 | (5) |
где n – объем выборки, количество измерений;
k – число разрядов (интервалов) статистического ряда;
 – эмпирическая (статистическая) частота появления случайной величины X (результата измерения) в i-ом интервале;
– эмпирическая (статистическая) частота появления случайной величины X (результата измерения) в i-ом интервале; 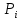 – вероятность попадания величины X в i-й интервал, рассчитанная по предполагаемому теоретическому распределению (в частности, для нормального закона распределения).
– вероятность попадания величины X в i-й интервал, рассчитанная по предполагаемому теоретическому распределению (в частности, для нормального закона распределения).Оформим вычисления в виде таблицы 4.
Таблица 4 – Результаты вычисления критерия
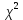
| i | ni | xi, xi+1 |  | 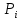 | 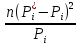 |
| 1 | 6 | 19,85;19,92 | 0,023 | 0,01045 | 3,9576 |
| 2 | 9 | 19,92;19,99 | 0,035 | 0,05045 | 1,2935 |
| 3 | 33 | 19,99;20,06 | 0,127 | 0,14674 | 0,6962 |
| 4 | 71 | 20,06;20,13 | 0,273 | 0,25755 | 0,2433 |
| 5 | 79 | 20,13;20,20 | 0,304 | 0,27298 | 0,9073 |
| 6 | 41 | 20,20;20,27 | 0,157 | 0,17474 | 0,4325 |
| 7 | 16 | 20,27;20,34 | 0,061 | 0,06751 | 0,1377 |
| 8 | 5 | 20,34;20,41 | 0,019 | 0,01573 | 0,2024 |
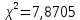 | |||||
-
Находим число степеней свободы распределения «хи-квадрат» по формуле (6):
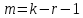 | (6) |
где k – число интервалов эмпирического распределения (вариационного ряда);
r – число параметров теоретического распределения, определяемых по опытным данным (в случае нормального закона распределения число оцениваемых по выборке параметров r = 2).
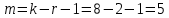
-
Для уровня значимости α = 0,02 по таблице 2 – распределения найдем критическое значение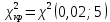 при числе степеней свободы m = 5.
при числе степеней свободы m = 5.
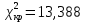
-
Так как фактически наблюдаемое значение 2 меньше критического, то гипотеза не противоречит опытным данным и закон распределения опытных данных можно считать нормальным. -
Запишем теоретический закон распределения и построим график плотности распределения вероятностей результатов измерения, как графическое представление теоретической плотности распределения.
Для описания теоретического закона распределения воспользуемся формулой (7), в которой неизвестные параметры распределения ???????? и ???????? заменим статистическими оценками числовых параметров нормального распределения ????∗ и S, рассчитанными в п.3:
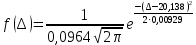 | (7) |
Для наглядности теоретический график плотности распределения вероятностей и гистограмму (как графическое представление статистической плотности распределения) построим на одной диаграмме.
Для приведения графиков статистического и теоретического распределений к одному масштабу используем нормированные значения
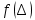 н.
н.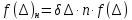
Где
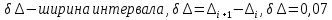
n - количество измерений.
Диаграмма представлена на рисунке 2.
Таблица 5 – Сводная таблица результатов измерений