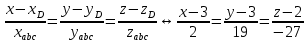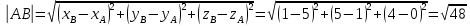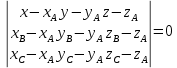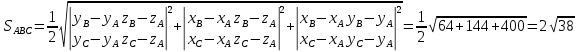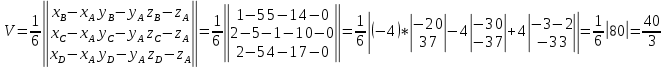Файл: Контрольная работа 1 Тарасов А. В. Омск 2022 Найти матрицу Dab2C.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 16

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая образовательная организация высшего

образования «Сибирский институт бизнеса и информационных технологий»

Дисциплина: высшая математика

Тема: Контрольная работа №1

Выполнил:

Тарасов А.В.

Омск 2022

8. Найти матрицу D=AB-2C





Находим произведение A*B



Матрицу С умножаем на 2 и получаем


Находим матрицу





18. Дана невырожденная матрица А. Найти обратную матрицу А-1 и пользуясь правилом умножения матриц, показать, что А*А-1=Е, где Е – единичная матрица.





Находим обратную матрицу





Перемножаем А*А-1





Получаем единичную матрицу, следовательно решение верно

28. Решить систему линейных уравнений с тремя неизвестными



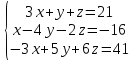
Запишем систему линейных уравнений в матричном виде для решения методом Крамера



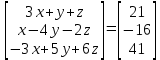
Получаем матрицу





Определитель матрицы равен







Находим x


=4


Находим y


=1


Находим z


=8


38. Построить треугольник, вершины которого находятся в точках А(0;4), В(-2;4), С(-2;-2).

Найти:

  1. Уравнения сторон треугольника АВС

  2. Координаты точки М пересечения медиан

  3. Длину и уравнение высоты, опущенной из вершины А

  4. Площадь треугольника

  1. Уравнения сторон треугольника находим по формуле

АВ:



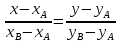
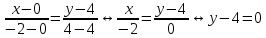
AC:



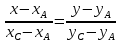
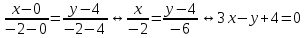
BC:





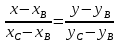
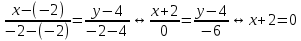
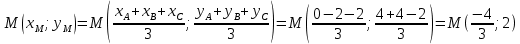
  2. Находим площадь треугольника



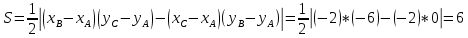
  1. Вычислим длину высоты опущенной из точки А



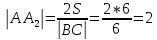
Составляем уравнение высоты АА2



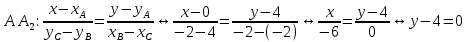
48. Даны координаты точек A(5;1;0), B(1;5;4), C(2;-1;0), D(2;4;7). Найти

  1. длину ребра АВ

  2. Уравнение плоскости, проходящей через точки А, В и С

  3. Уравнение высоты опущенной из точки D на плоскость АВС

  4. Площадь грани АВС

  5. Объем пирамиды ABCD

Решение:





Подставляем значения и получаем: (x-5)(4*0-4*(-2))-(y-1)((-4)*0-4*(-3))+(z-0)((-4)*(-2)-4*(-3))=0

8x-12y+20z-28=0

2x-3y+5z-7=0

  1. Уравнение высоты опущенной из точки D на плоскость ABC выглядит следующим образом






Смотрите также файлы