ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2021
Просмотров: 123
Скачиваний: 1
Будівельна механіка в прикладах і задачах
Спеціальність – 0921 – “Будівництво”
Тема: Статично визначена арка
Лекція №2. Розрахунок статично визначеної арки на сталі навантаження та побудова ліній впливу.
Мета і задачі:
Метою теми є вміння визначати напружений стан в перетинах статично визначеної арки – одного із основних конструктивних елементів конструкцій.
Для досягнення мети необхідно вирішення наступних задач:
1. Визначення реакцій в опорних зв’язках за допомогою рівнянь статики.
-
Побудова епюр поперечних сил та згинальних моментів в аналогічній балці такого ж прогону, як в арці, що знаходиться під дією такого ж навантаження.
-
Призначення характерних перерізів, визначення в них декартових координат та кутів нахилу їх до горизонту.
-
Визначення зусиль в арці за формулами (2.1), заповнення таблиці 2.1 та побудова епюр M, Q, N.
-
Побудова ліній впливу опорних реакцій та ліній впливу M, Q, N для
довільного перерізу арки.
-
Перевірка аналітичного розрахунку з розрахунком зусиль за лініями впливу.
2.1 Розрахунок статично визначеної арки на сталі навантаження

http://www.youtube.com/watch?v=GwwpbWLXI3o Область
практичного впровадження арки
http://www.youtube.com/watch?v=TM0VPbSwQvA Область
практичного впровадження арки
2.1.1 Визначення реакцій в арці
Розрахункову схему статично визначеної арки подано на рис.2.1. Реакції в зв’язках арки знаходяться за допомогою рівнянь статики:
;
.
.
2.1.2 Перевірка реакцій за лініями впливу:
До розрахункової схеми арки на рис.2.1 прикладено зосереджене та розподілене навантаження. За умови дії на схему довільних видів стаціонарного навантаження лінії впливу як реакцій так і внутрішніх зусиль знаходяться за формулою:
де
- зосереджені сили,
- ордината лінії впливу досліджувального
фактора під точкою прикладання
зосередженого навантаження;
- інтенсивність
розподіленого навантаження,
-
площа лінії впливу під розподіленим
навантаженням;
-
зосереджений момент,
- тангенс кута нахилу лінії впливу до
горизонту в точці дії зосередженого
момента.
.
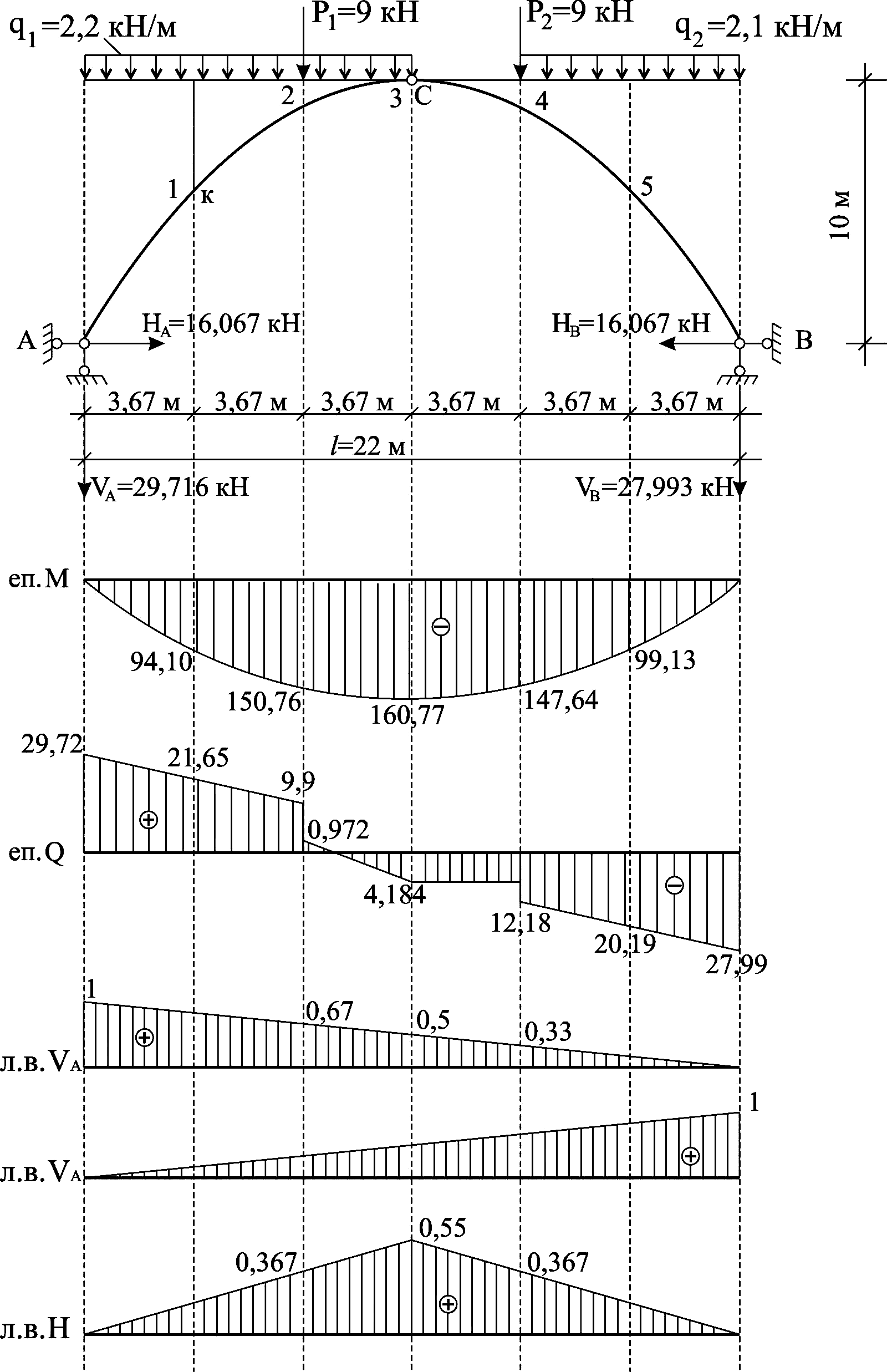
Рисунок 2.1 – Побудова епюр M0, Q0 в аналогічній балці та ліній впливу опорних реакцій в арці 2.1.3 Побудова кінцевих епюр згинальних моментів, поперечних сил та поздовжніх сил в арці від дії вертикальних сил
Внутрішні зусилля в арці визначаються за формулами:
,
,
,
(2.1)
де
– поперечна сила та згинальний момент
в аналогічній балці, такої ж довжини
та під таким же навантаженням.
Починається розрахунок призначенням характерних перерізів, для яких, за формулами квадратної параболи, знаходяться відповідні координати х, у.
.
(2.2)
Для знаходження кута нахилу j дотичної до горизонту в характерних перерізах використано залежність
tgj
=
;
(2.3)
б) дані розрахунків внутрішніх зусиль наведено в таблиці 2.1.
Таблиця 2.1
|
№ пере-різу |
Координати |
градуси |
|
|
|
M |
|
|
N |
|
|
x |
y |
|||||||||
|
A |
0 |
0 |
61,2 |
0,876 |
0,482 |
0 |
0 |
29,7 |
0,24 |
-33,8 |
|
1(k) |
3,67 |
5,55 |
50,5 |
0,782 |
0,636 |
94,2 |
4,93 |
21,65 |
1,36 |
-26,94 |
|
2 |
7,33 |
8,86 |
31,3 |
0,52 |
0,854 |
158,76 |
16,18 |
13,6 4,6 |
3,9 -4,45 |
-20,8 -16,1 |
|
C(3) |
11 |
10 |
0 |
0 |
1 |
160,8 |
0 |
-3,48 |
-3,48 |
-16,08 |
|
4 |
14,67 |
8,87 |
-31,3 |
-0,52 |
0,854 |
147,67 |
5,06 |
-3,48 -12,48 |
5,38 -2,3 |
-15,5 -20,2 |
|
5 |
12,33 |
5,55 |
-50,5 |
-0,772 |
0,636 |
88,13 |
-1,12 |
-20,18 |
-0,375 |
-25,81 |
|
B |
22 |
0 |
-61,2 |
-0,876 |
0,482 |
0 |
0 |
-27,88 |
0,645 |
-32,19 |
HA=HB=H=16.08 кН.
т.
А
т.1
т.2
т.3
,
т.4
т.5
т.В
.
З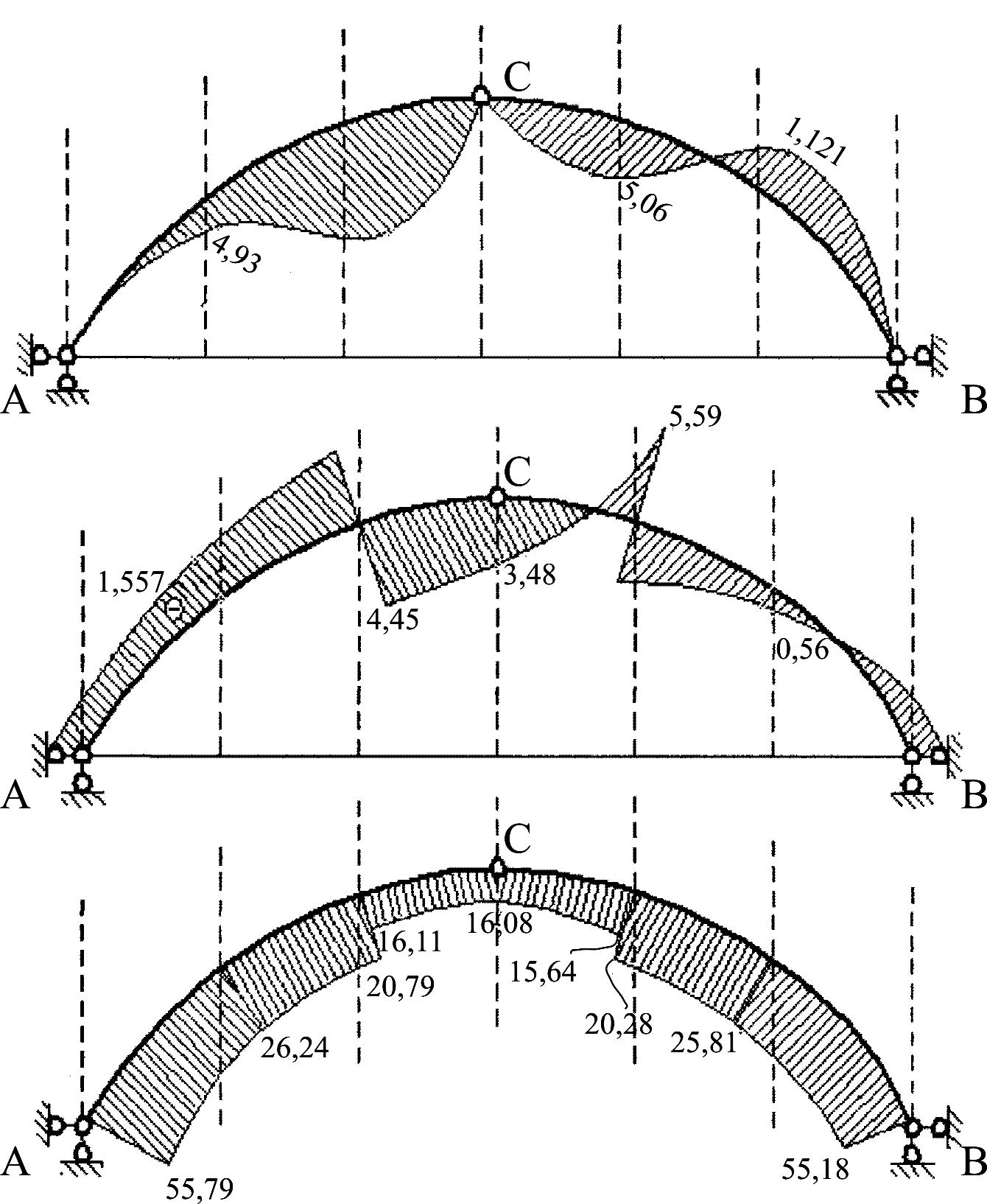 а
даними розрахунків таблиці 2.1 будуємо
кінцеві епюри M, Q, N в
статично визначеній арці.
а
даними розрахунків таблиці 2.1 будуємо
кінцеві епюри M, Q, N в
статично визначеній арці.

Рисунок 2.2 – Кінцеві епюри M, Q, N в статично визначеній арці
2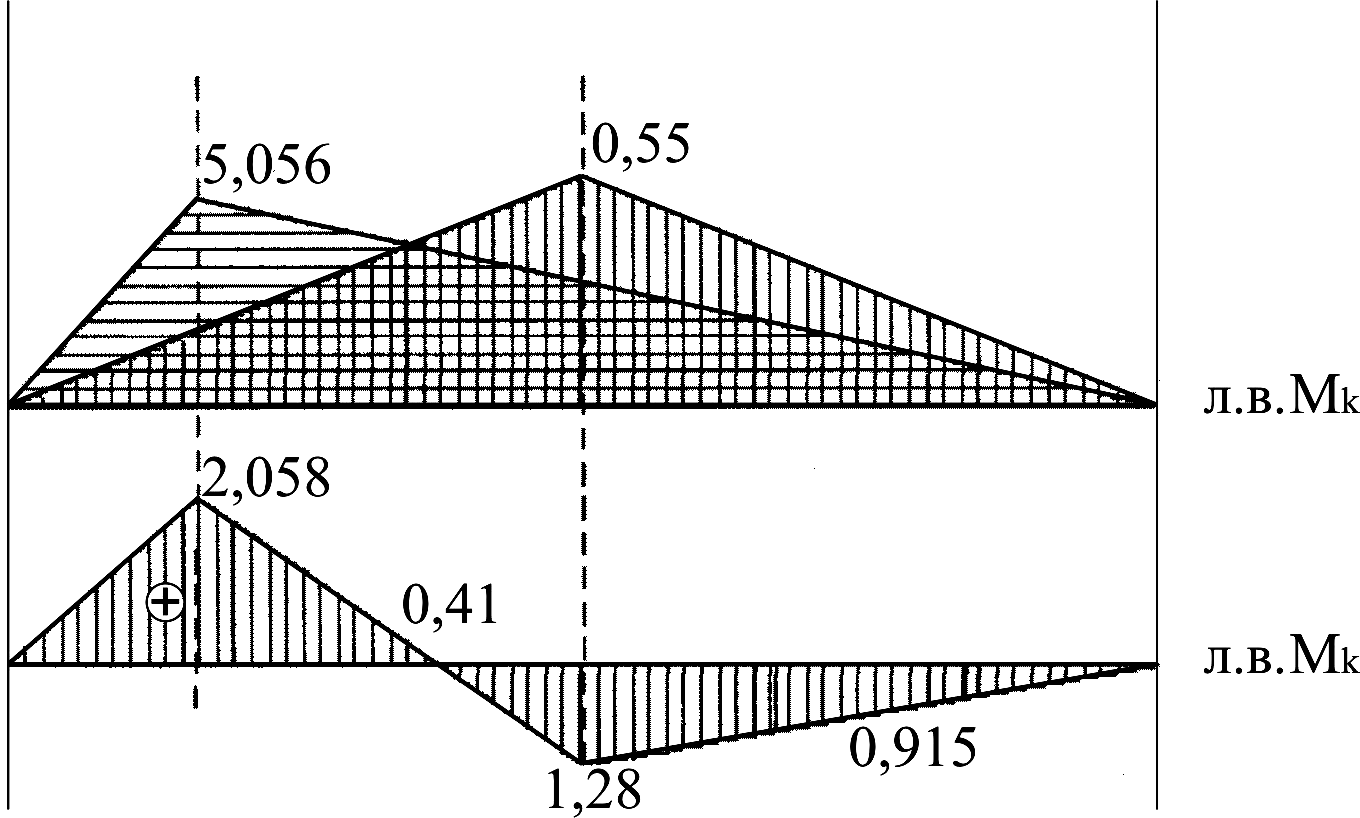 .2
Побудова ліній впливу в арці,
визначення зусиль за лініями впливу та
порівняння з аналітичним розрахунком
.2
Побудова ліній впливу в арці,
визначення зусиль за лініями впливу та
порівняння з аналітичним розрахунком
Рисунок 2.3 – Побудова лінії впливу згинального моменту в перерізі 1
Зусилля згинального моменту в арці в перерізі 1 за лінією впливу:
Рисунок 2.4 – Побудова лінії впливу поперечної сили в перерізі 1 арки
Поперечна сила в перерізі 1 в арці за лінією впливу:
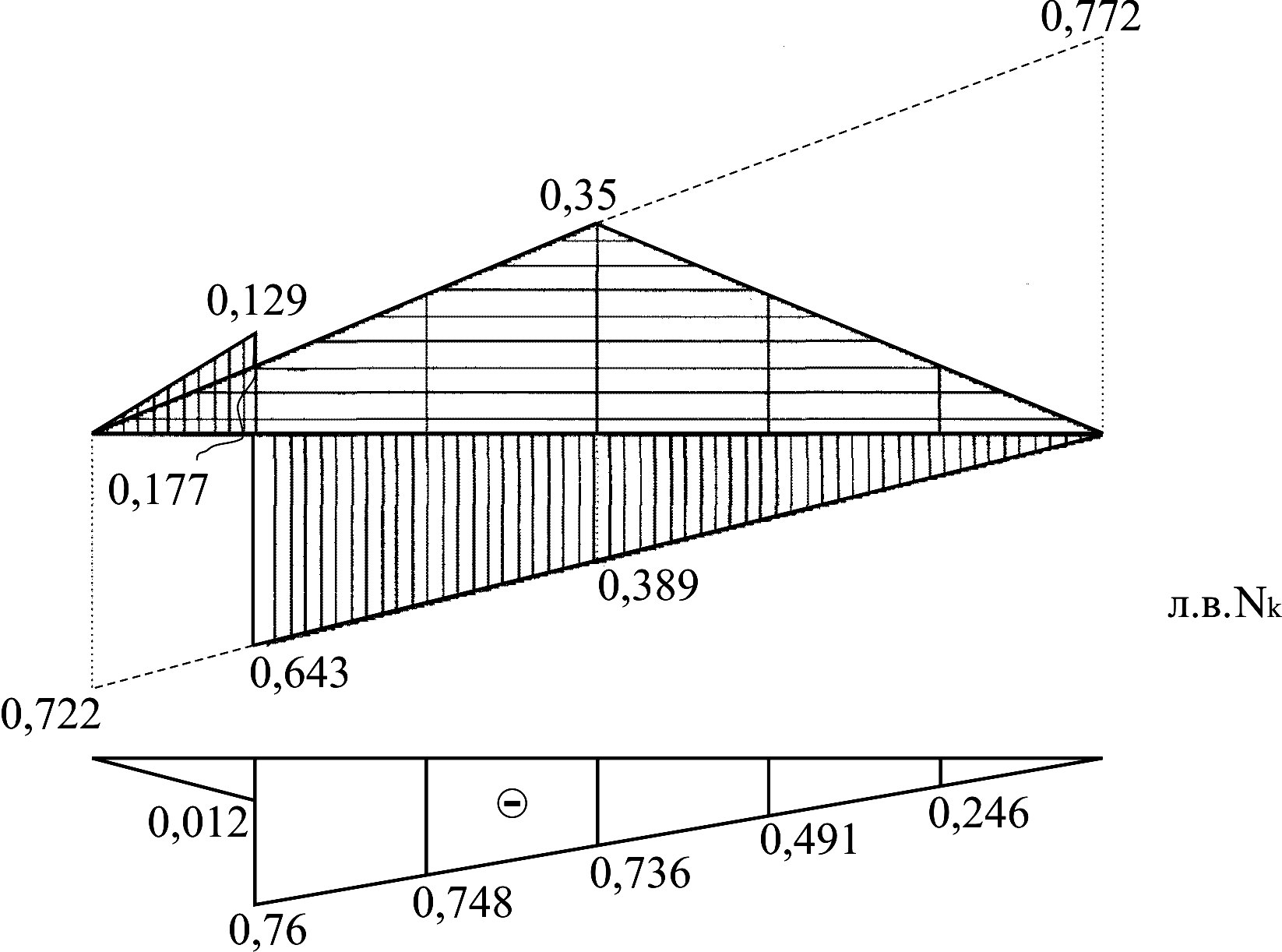
Рисунок 2.5 – Побудова лінії впливу поздовжної сили в перерізі 1арки
Зусилля поздовжної сили в перерізі 1 в арці за лініями впливу:
Підсумок.
Після проходження даної лекції студент має вміти знаходити реакції в арці як вертикальні, так і горизонтальні, будувати еп. М,Q,N, будувати лінії впливу та визначати за ними зусилля в арці.
Контрольні питання.
1.Як визначати вертикальні та горизонтальні складові реакцій в арці ?
2. Яке додаткове статичне рівняння рівноваги потрібно записати для визначення горизонтальної складової (розпору) в арці?
3.За якими аналітичними залежностями визначаються внутрішні зусилляя в арках ?
4.Що називають лінією впливу, як їх будувати та як визначати за ними зусилля в арках?
Джерела інформації.
1. Баженов В.А., Іванченко Г.М., Шишов О.В. Будівельна механіка. Розрахункові вправи. Задачі. Компютерне тестування.-К.: “Каравелла”, 2006.-344с.
2. Баженов В.А., Гранат С.Я., Шишов О.В. Будівельна механіка. Компютерний курс.-К.: Вища школа, 1999.-540с.
3. Баженов В.А. Будівельна механіка.-К.: Вища школа, 2000.-670с.
4. Бутенко Ю.Н. Строительная механика. – К.:”Вища школа”, 1989,- 480с.
5. Бутенко Ю.И. Строительная механика. Руководство к практическим занятиям. - К.: Вища школа, 1984.- 327 с
6. Дарков А.В. Шапошников Н.Н. Строительная механика. - М.:”Высшая школа”, 1986,-607с.
7. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем). – М.:”Высшая школа”, 1980, -384с.
8. Моргун А.С. Теорія споруд, ч. ІІІ, Будівельна механіка – Вінниця:
ВДТУ,1997,90 с.
9. Моргун А.С. Практикум з будівельної механіки. – Вінниця: ВДТУ, 1997,90 с.
10. Піскунов В.Г. Опір матеріалів з основами теорії пружності і пластичності. Ч.І. Книга 3. Опір дво- і тривимірних тіл. - К.: Вища школа, 1995.- 272 с.
Глосарій.
1. Характерні ператини – визначальні перетини, в яких розраховуються внутрішні зусилля.
2. Правило карандаша – формулювання для визначення знаку еп.Q за еп. М.
3. Лінія впливу – графік, що показує закон зміни досліджувального фактора (згинального моменту, поперечної сили, реакції, подовженої сили) в залежності від положення на балці рухомого одиничного навантаження Р=1.