Файл: Решение npтрудных задач комбинаторной оптимизации.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 7

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




Лабораторная работа №1

Тема: Решение NP-трудных задач комбинаторной оптимизации

Задание:

1. Решить задачу о коммивояжере и описать алгоритм для ее решения.

2. Провести численные эксперименты на тестовых примерах из международной библиотекиOR-library (можно в Интернете в поисковике набрать OR-library, сделав выводы по экспериментам. (http://people.brunel.ac.uk/mastjjb/jeb/info.html),
Задача коммивояжера (TSP): имеется n городов, известны расстояния между каждой парой городов. Найти наименьший маршрут, начинающийся и оканчивающийся в некотором базовом городе и проходящий по одному разу через все города.

Математическая модель задачи коммивояжера

Пусть - полный ориентированный граф, где - множество вершин – городов, - множество ребер (участков дорог). Каждому ребру сопоставлено число - расстояние между парой городов.

Введем переменные

Найти маршрут наименьшей длины :

(только одно ребро должно выходить из каждой вершины)

(только одно ребро должно входить в каждую вершину)

, (запрещены замкнутые маршруты)

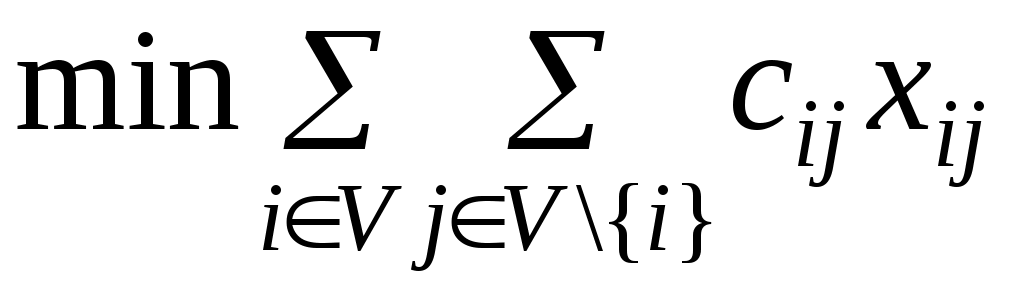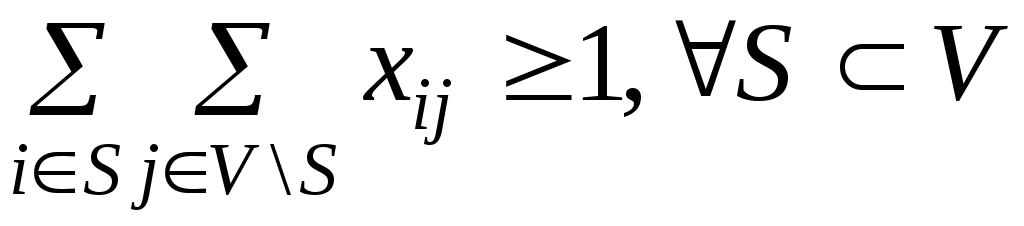Искомую матрицу можно преобразовать в перестановку чисел L*, которую принять за решение задачи: L*
= {i1, i2,…, in}.

2. Общая схема алгоритмов (+) –ЕА, (, )–ЕА ( - число особей,  - число потомков, tmax– количество итераций)

1. Построить начальную популяцию П0 = ( )

2. Вычислить функцию пригодности

3. Для t:=0 до tmax – 1 выполнить:

3.1. Для j:=1 до  выполнить:

3.1.1. u – случайная величина из {1,…, } c равномерным распределением

3.1.2.
3.2.

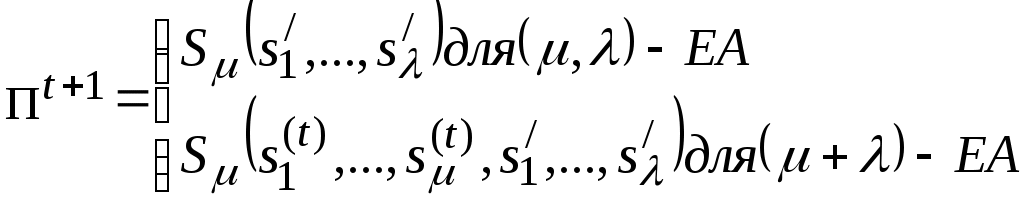
3.3. t:=t+1

4. Получить лучшее из найденных решений

Общая схема алгоритма (1+1) –ЕА

  1. Сгенерировать решение s0

  2. Для t:=0 до tmax –1 выполнить:

    1. s’ =Мутация (st)

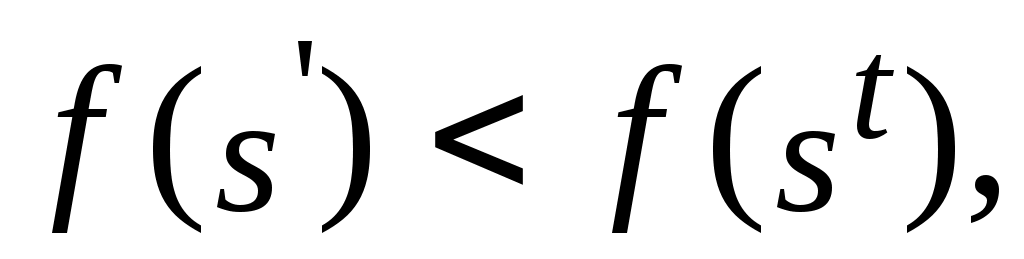    2. Если то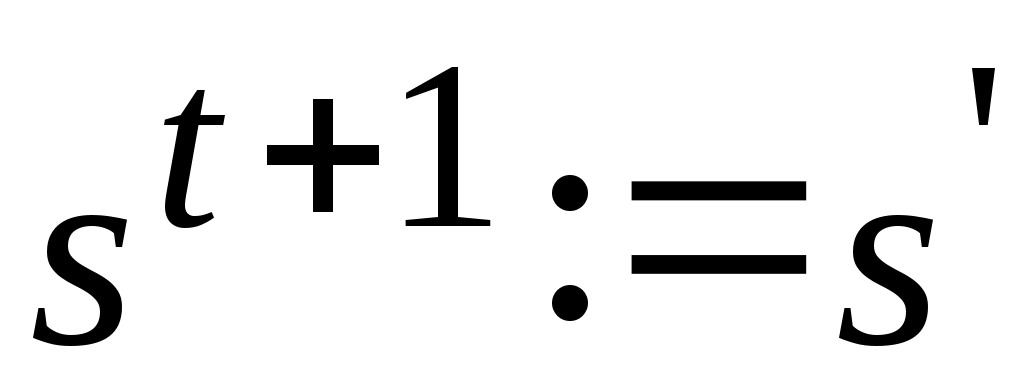

2.1. Если то с вероятностью р,

иначе

2.2. t:=t+1

3. Лучший результат работы алгоритма

Пример применения алгоритма (1+1)–ЕА

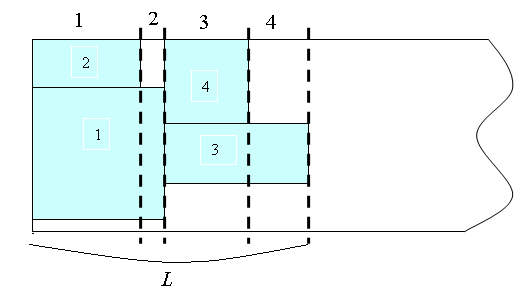Дано: полубесконечная полоса ширины W, размеры прямоугольников . Требуется разместить прямоугольники в полосу так, чтобы длина занятой части полосы была минимальной.



Карта размещения прямоугольников, s0
Исходное допустимое решение s0;

Приоритетный список ПС=(2,1,4,3) (кодировка решения);

Длина занятой части полосы: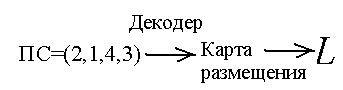

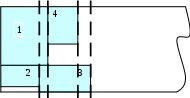=l2+ (l1–l2)+l4+(l3 - l4)




Рис. 2. Новое решение



  • Применим к решению s0 мутацию – поменяем местами два случайно выбранных элемента ПС, например, 2 и 1.

  • Тогда новое решение будет: ПС1=(1,2,4,3) (см. рис. 2).

  • Если (ПС1) < (ПС), то на следующем шаге алгоритма выбирается решение ПС1=(1,2,4,3).

3. Пример оформления экспериментов:

Пример задачи. Решалась задача размещения кругов в полубесконечную область ширины алгоритмом муравьиной колонии ACOGA.

Цель эксперимента в определении лучших параметров алгоритма: коэффициентов влияния эвристической информации β и уровня феромона α на значения целевой функции.

Серия 1.

  • Коэффиценты α и β изменялись на интервале от 0,4 до 2-х с шагом 0,1; количество агентов m=12; размер популяции k=10; начальное значение феромона τinit =0,05.

  • Эксперимент проводился на тестовых примерах из международной библиотекиOR-library (http://people.brunel.ac.uk/mastjjb/jeb/info.html) класса С1,содержащего три примера С11, С12, С13, в которых количество кругов равно 100. Радиусы кругов (ric – радиус i-го круга) были случайно сгенерированы в интервале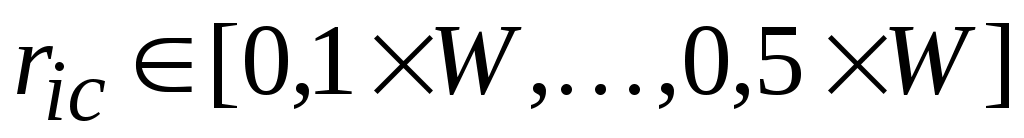 . На рис. 3 приведены значения целевых функций (по оси Y) при некоторых значениях коэффициентов α и β.

  • Вывод. В результате проведения эксперимента было выявлено, что наилучшими значениями являются коэффициенты α=1,6 и β=0,6, поскольку на этих коэффициентах алгоритм дал наилучшие решения почти на всех примерах класса С1.


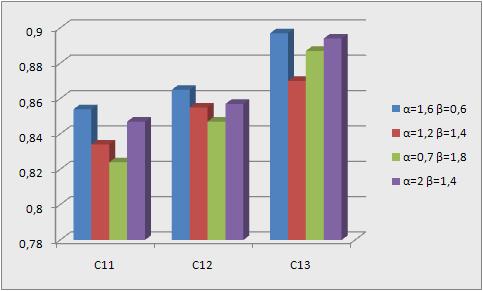
Рис. 3. Влияние параметров α и β на качество решений

Серия 2.

  • Цель эксперимента в сравнении результатов, полученных алгоритмом ACOGA с результатами других алгоритмов: генетическим алгоритмом CAGA, методом ветвей и границ S.Y., жадной эвристической процедурой В1.5, алгоритмом вероятностного поиска с запретами TABU SEARCH (TS), коммерческим пакетом GAMS (http://www.gams.com/), а также с LB – нижней оценкой оптимальной длины полосы,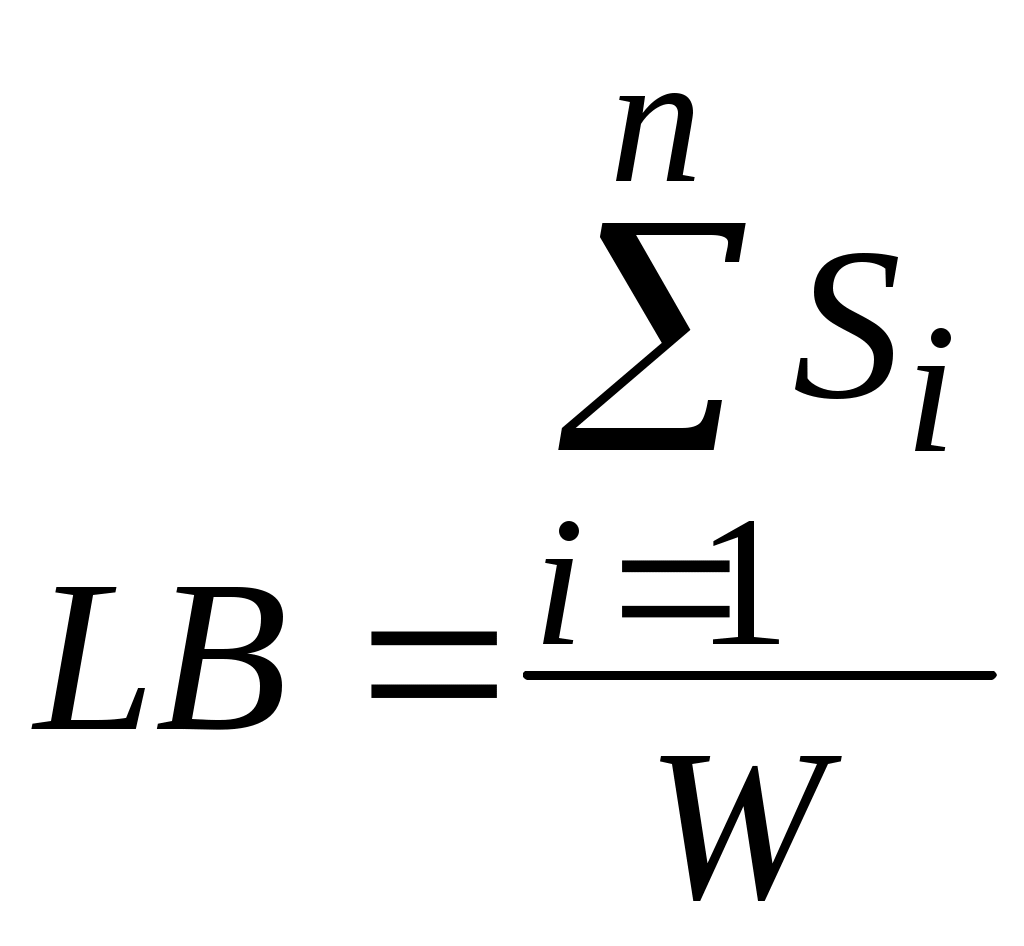 ( 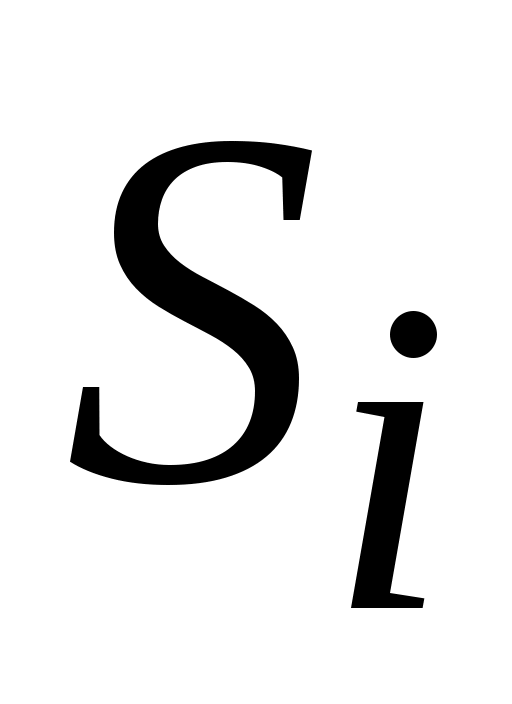–площадь 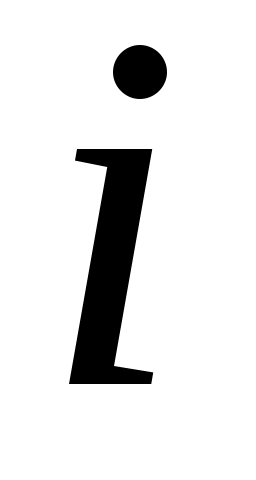–го круга). Тестовые примеры SY1-SY6 брались из библиотеки OR-library. В качестве критерия оценки выступает длина занятой части полубесконечной области L. На рис. 4 приведены значения целевых функций (по оси Y) для рассматриваемых алгоритмов.

  • Вывод. Как видно из результатов численного эксперимента, алгоритм ACOGA в большинстве случаев находил решения лучше, чем алгоритмы B1.5 и S.Y. С алгоритмом TS алгоритм ACOGA находил одинаково хорошие решения



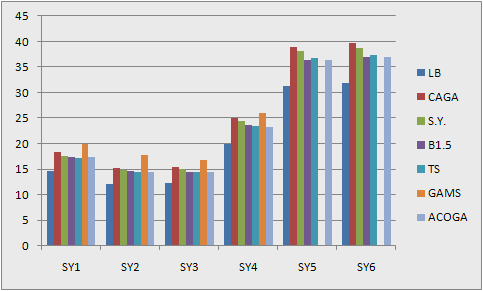
Рис. 4.

Смотрите также файлы