Добавлен: 10.11.2023
Просмотров: 35
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт машиностроения
(наименование института полностью)
Кафедра "Сварка, обработка материалов давлением и родственные процессы"
(наименование кафедры/департамента/центра полностью)
15.03.01 Машиностроение
(код и наименование направления подготовки, специальности)
Технологии сварочного производства и инженерия поверхностей
(направленность (профиль) / специализация)
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №6
по учебному курсу «Высшая математика 2»
Вариант 1
| Студент | Перлухин А. В. (И.О. Фамилия) |
| Группа | ПИдб-2105а |
| Преподаватель | Лисненко А. П. (И.О. Фамилия) |
Тольятти 2023
| № п/п | Задача | Ответ |
| 1 | Составить уравнение линии уровня u = C и построить ее график: | |
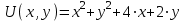 , С = -4 , С = -4 | 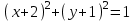 | |
| Решение: Выделим полные квадраты в правой части исходной функции: 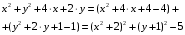 Т.о. уравнение искомой линии уровня имеет вид: 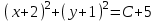 . .Это уравнение определяет систему концентрических окружностей с центром в точке (-2;-1) и переменным радиусом 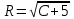 . . При заданном значении константы С = -4 получаем окружность единичного радиуса с центром в точке (-2; -1). | ||
| График: 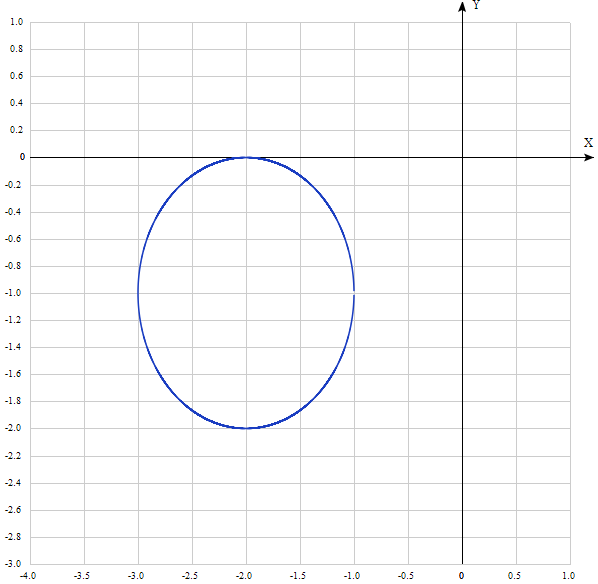 | ||
| 2 | Вычислить с помощью градиента производную скалярного поля 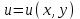 в точке А по направлению вектора в точке А по направлению вектора 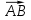 : : | |
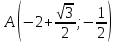 , , 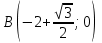 , ,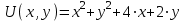 | 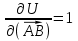 | |
| Решение: По определению градиента: 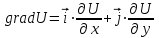 Находим частные производные: 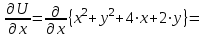 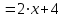 ; ;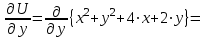 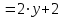 ; ;Тогда градиент скалярного поля равен: 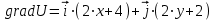 Градиент поля U в точке А: 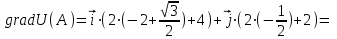 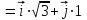 ; ;Определяем координаты вектора АВ: 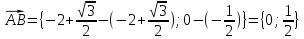 Модуль вектора АВ: 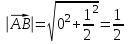 ; ;Производная скалярного поля U в точке А по направлению вектора АВ определяется соотношением: 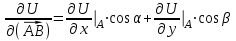 где направляющие косинусы равны: 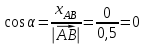 ; ; 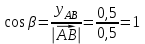 . .Тогда производная скалярного поля U в точке А по направлению вектора АВ равна: 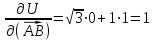 . . | ||