ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехнических систем и обработки сигналов

Дисциплина «Компьютерное моделирование и проектирование систем ЦОС»

Лабораторная работа № 09

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (часть 1)

Выполнили: ст. гр. РТ-82

Кравцова А. А.

Сырорыбрв В. А.

Проверил: ст. пр. Чернов И.Н.

________________
Цель работы: изучить дискретное преобразование Фурье (ДПФ) периодических последовательностей и последовательностей конечной длины и овладеть программными средствами его вычисления в MATLAB

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение	Идентификатор
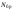	Номер бригады		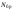Nb = 3
	Период (длина) последовательности		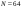N = 64
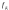	Частота дискретизации		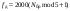Fs = 8000
	Период дискретизации		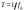1/8000
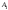	Амплитуды дискретных гармоник		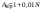A1 = 1,03
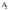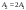			A2 = 2,06
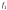	Частоты дискретных гармоник		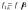f1 = 1000
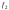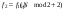			f2 = 3000

---

ФОРМУЛЫ ДПФ

Прямое ДПФ:



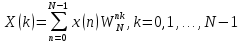
Обратное ДПФ:



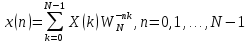
Где

• 
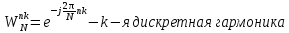
  ДПФ X(k) одновременно описывает и спектр периодической последовательности (с точностью до множителя 1/N), и спектральную плотность конечной последовательности.
  
• 
  Для периодической последовательности x(n) с периодом N ДПФ X(k) представляет собой ее спектр с точностью до множителя 1/N.
  
  
• 
  Для конечной последовательности x(n) длины N ДПФ X(k) представляет собой N дискретных равноотстоящих значений ее спектральной плотности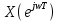 на периоде д   2/T .
  
  

1. 
   Вычисление амплитудного и фазового спектров периодической последовательности.
   

% Для вывода ИСХОДНЫХ АМПЛИТУД и ЧАСТОТ ДИСКРЕТНЫХ ГАРМОНИК нажмите

%

A1 = 1.03 A2 = 2.06

f1 = 1000 f2 = 3000



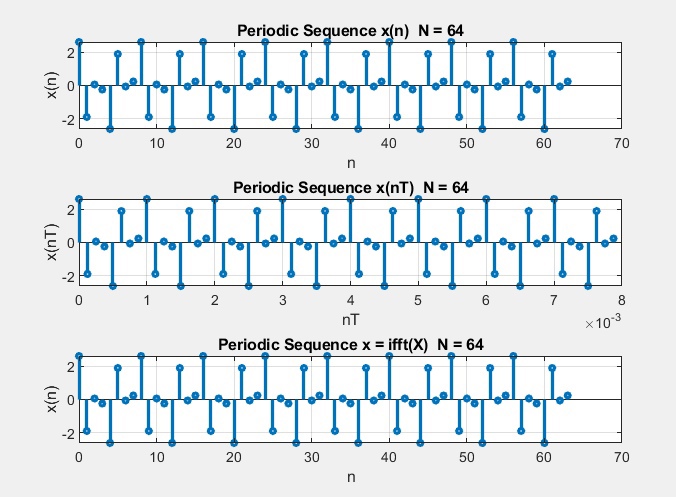
рис. 1 Графики периодической последовательности

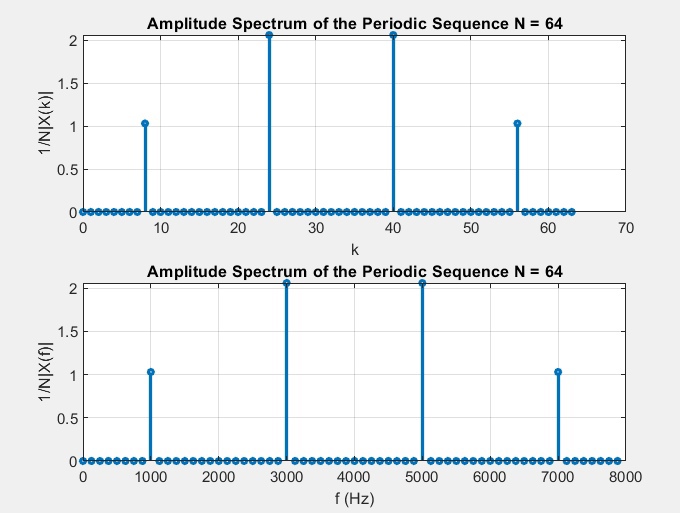рис.2 Графики амплитудного спектра периодической последовательности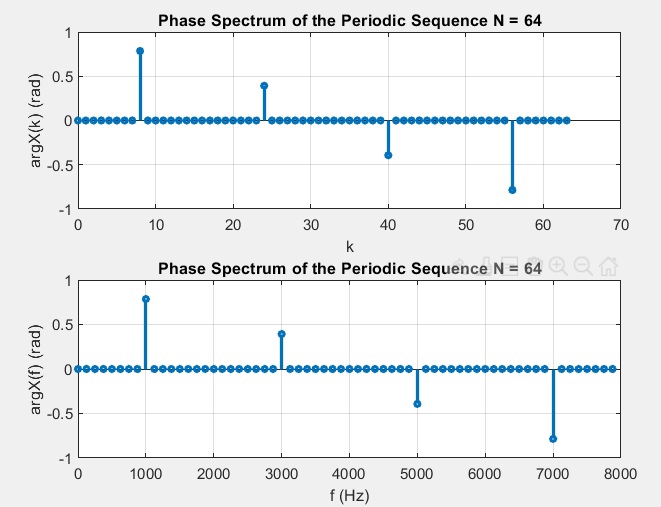


рис. 3 Графики фазового спектра периодической последовательности

• 
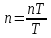  , где 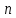- дискретно нормированное время, 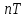- нормированное время, 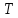- период дискретизации
  
• 
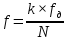  , где 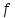- абсолютная частота 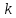- дискретно нормированная частота,
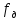  – частота дискретизации, 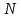- длина последовательности
  
  
• 
  амплитудный и фазовый спектры являются дискретными
  

2. 
   Вычисление ДПФ конечной последовательности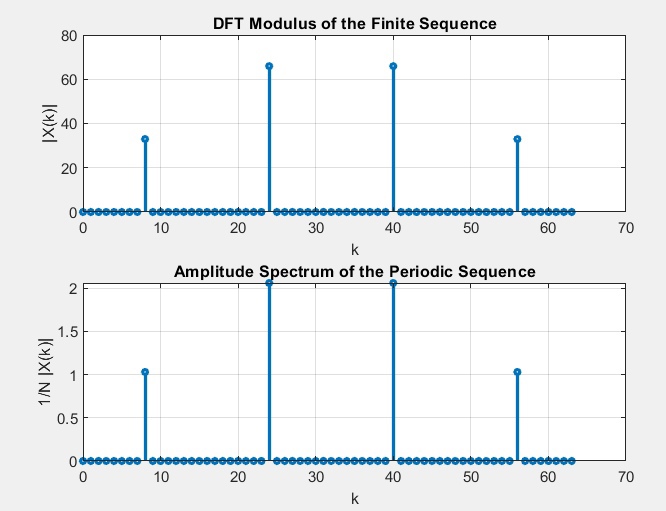
   
   

рис. 4 Графики модуля ДПФ конечной последовательности и амплитудного спектра периодической последовательности

• 
  Амплитудный спектр вещественной периодической последовательности равен модулю ДПФ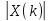 с точностью до множителя:
  

3. 
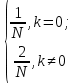
   Определение амплитуд и частот дискретных гармоник
   

% Для вывода ВЫХОДНЫХ ПАРАМЕТРОВ ФУНКЦИИ fft_e1 нажмите

MODm =

1.0300 2.0600 2.0600 1.0300

m =

8 24 40 56

%

%

% Для вывода АМПЛИТУД и ЧАСТОТ ДИСКРЕТНЫХ ГАРМОНИК нажмите

%

%

A1 = 1.03 A2 = 2.06

k1 = 8 k2 = 24

f1 = 1000 f2 = 3000

%

%

% СРАВНИТЕ с ВЫХОДНЫМИ ПАРАМЕТРАМИ функции fft_e1 и исходными данными

Выходные параметры функции и исходные данные совпадают

• 
  MODm –значения амплитуд абсолютных частот
  m –амплитуды дискретных нормированных частот
  A1, A2 – амплитуды дискретных гармоник
  

k1, k2 – дискретные нормированные частоты

f1, f2 – абсолютные частоты дискретных гармоник

• 
  Соответствует отношению: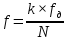
  
  

4. 
   Граничные значения порогов для первого и второго критериев выделения полезного сигнала
   

% Для вывода граничных значений порога для ПЕРВОГО КРИТЕРИЯ нажмите

%

%

e1_low = 0.27211 e1_up = 1

%

%

% Для вывода граничных значений порога для ВТОРОГО КРИТЕРИЯ нажмите

%

%

e2_low = 1.4572 e2_up = 19.6794

• 
  Нижняя граница порога для первого критерия рассчитывается как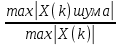
  , верхняя граница порога для первого критерия равна 1.
  
• 
  Нижняя граница порога для второго критерия равна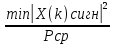
  , верхняя граница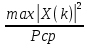
  

5. 
   Выделение полезного сигнала по первому критерию
   

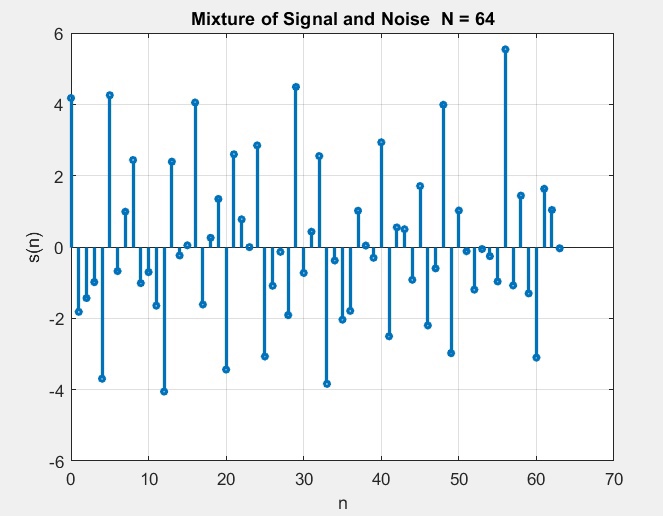рис. 5 График аддитивной смеси сигнала с шумом

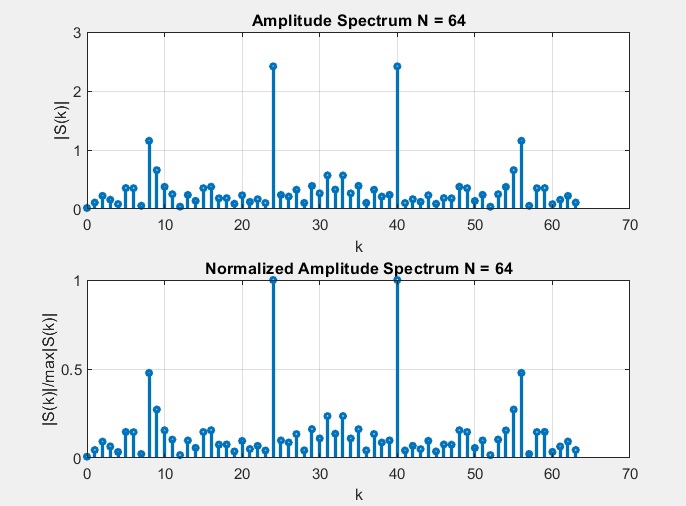рис. 6 Графики амплитудного и нормированного амплитудного спектров аддитивной смеси сигнала с шумом

% Введите выбранное значение порога e1 для ПЕРВОГО КРИТЕРИЯ

%

e1 = 0.5

%

% Для вывода ВЫХОДНЫХ ПАРАМЕТРОВ ФУНКЦИИ fft_e1 нажмите

MODm =

2.4171 2.4171

m =

24 40

%

% СРАВНИТЕ значения ВЫДЕЛЕННЫХ ПО ПЕРВОМУ КРИТЕРИЮ АМПЛИТУД И ЧАСТОТ

% с исходными данными

-выделенные амплитуды и частоты примерно совпадают с максимумами исходных амплитуд и частот.

• 
  Выбранное значение порога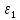 равное 0,5 попадает в диапазон между нижним и верхним порогами для первого критерия.
  
• 
  Если модуль ДПФ, нормированный к его максимального значению, выше порогового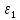 , то текущую гармонику относят к полезному сигналу.
  
• 
  Согласно первому критерию, полезному сигналу соответствуют амплитуды абсолютной частоты дискретного сигнала и дискретные нормированные частоты равны 2,4171; 24 и 40 соответственно.
  
• 
  Применение первого критерия будет неэффективным, если не выполняется условие: .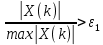
  

6. 
   Выделение полезного сигнала по второму критерию
   

рис. 7 Графики амплитудного спектра и квадрата амплитудного спектра, нормированного к величине средней мощности аддитивной смеси сигнала с шумом
% Введите выбранное значение порога e2 для ВТОРОГО КРИТЕРИЯ

%

e2 = 5

%

% Для вывода ВЫХОДНЫХ ПАРАМЕТРОВ ФУНКЦИИ fft_e2 нажмите

MODm =

2.4171 2.4171

m =

24 40

%

%

% СРАВНИТЕ значения ВЫДЕЛЕННЫХ ПО ВТОРОМУ КРИТЕРИЮ АМПЛИТУД И ЧАСТОТ

% с исходными данными

-выделенные амплитуды и частоты примерно совпадают с максимумами исходных амплитуд и частот.

• 
  Выбранное значение порога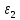 равное 5, соответствует диапазону между нижним и верхним порогами для первого критерия.
  
• 
  При заданном пороге 2 ε значение модуля ДПФ X k( ) относят к полезному сигналу, если выполняется условие: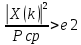
  
  
• 
  Согласно второму критерию, полезному сигналу соответствуют амплитуды абсолютной частоты дискретного сигнала и дискретные нормированные частоты равны 2,3054; 16 и 48 соответственно.
  
• 
  Применение второго критерия будет неэффективным, если не выполняется условие: .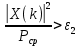
  

7. 
   Восстановление аналогового сигнала
   

рис. 8 Графики последовательности и модуля ее ДПФ, восстановленного аналогового и его спектра и исходного аналогового сигнала

• 
  Аналоговый сигнал с финитным спектром может быть точно восстановлен по отсчетам ДПФ: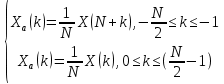
  
• 
  Восстановленный и исходный сигналы идентичны.
  

8. 
   Восстановление спектральной плотности конечной последовательности
   

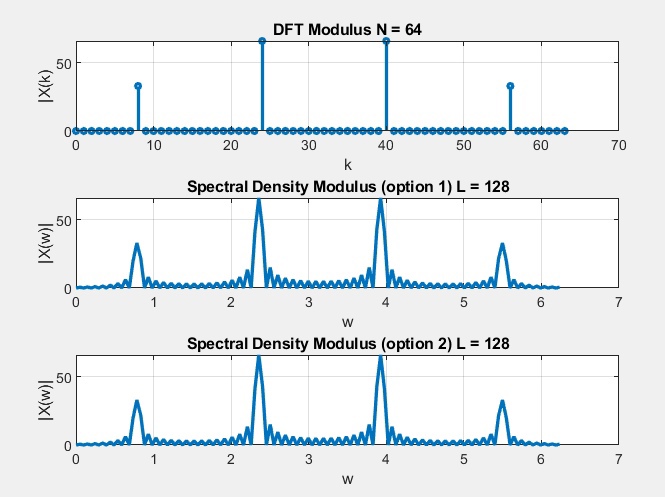рис. 9 Графики ДПФ и спектральной плотности конечной последовательности, вычисленной двумя способами

• 
  По N отсчётам ДПФ гарантируется точное восстановление спектральной плотности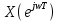 конечной последовательности длины N: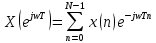
  

• 
  
  

9. 
   Уменьшение периода дискретизации по частоте при вычислении ДПФ
   

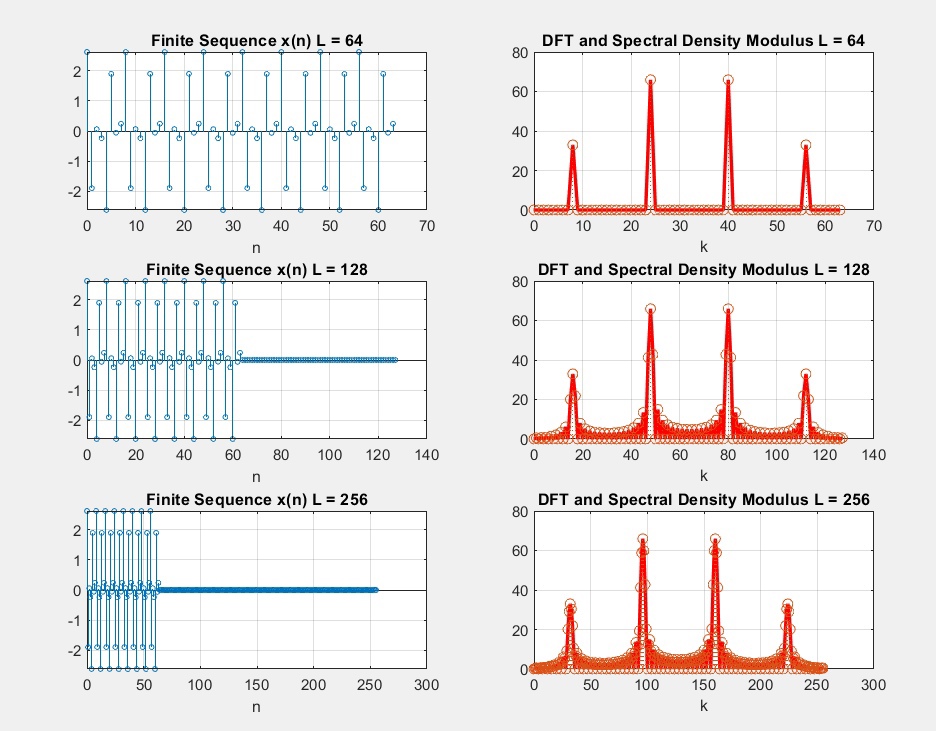рис. Графики конечных последовательностей, ДПФ и спектральных плотностей

% Для вывода ПЕРИОДОВ ДПФ и ПЕРИОДОВ ДИСКРЕТИЗАЦИИ ПО ЧАСТОТЕ нажмите

L = [64 128 256]

Delta_f = [125 62.5 31.25]

• 
  Период дискретизации по частоте зависит от количества дискретных точек.
  
• 
  Разрешение по частоте не изменится
  
• 
  
  
• 
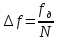
  Для улучшения различения близко расположенных гармоник
  Вывод: мы изучили дискретное преобразование Фурье (ДПФ) периодических последовательностей и последовательностей конечной длины и овладеть программными средствами его вычисления в MATLAB
  
  

Санкт-Петербург

2021

---

Смотрите также файлы

• Основным преимуществом горизонтального способа бурения и соответственно разработки месторождений с использованием горизонтальных стволов явилось многократное увеличение дебита скважин.docx

• Академик С. А. Джиенкулов атындаы Байоыр жоары колледжі білім беру мекемесі Бекітемін Арнайы пндер бірлестігіні жетекшісі.docx

• Устный последовательный перевод и его особенности уги124006.pptx

• Берілген жауаптарды ішінде html бойынша айсысы валидтілік болып есептеледі.docx

• Практическая работа 4. Разработка контентплана на учебный период.doc