Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Саратовский государственный технический университет имени Гагарина Ю.А.»

Кафедра «Прикладная математика и системный анализ»

Лабораторная работа №1
Систематизация, графическое представление статистических данных, выборочные числовые характеристики на основе большой выборки.

Выполнил:

студент гр. ИБС-21

Проверил:

доцент ПМиСА

Саратов, 2023

Лабораторная работа №1.

Систематизация, графическое представление статистических данных, выборочные числовые характеристики на основе большой выборки. Работа основана на материале лекций №1 и №2.

Цель работы: овладение приемами первичной обработки большой выборки. Выдвижение

гипотезы о законе распределения генеральной совокупности.

Средства вычислений: Персональный компьютер

Содержание работы: Для обработки из берем выборку объема n=100 элементов. Выборка оформляется в виде таблицы 1.

Нормальные N(0,1) распределенные случайное числа. Таблица 1.

20	26	32	34	26	28	22	30	17	24
30	28	18	22	24	26	34	28	22	20
34	24	28	20	32	17	22	24	26	30
30	22	26	35	28	24	30	32	28	18
20	30	17	24	32	28	22	26	24	30
34	26	24	28	22	30	35	32	20	17
28	22	36	30	20	26	28	23	24	32
20	26	30	24	32	17	22	28	35	26
28	35	32	22	26	24	26	24	30	24
18	24	26	28	35	30	26	22	26	28

---

Первичную выборку подвергаем обработке.

1. Систематизация

1. 
   Находим х_min, х_max.
   

х_{min = 17,} х_{max= 36}

2. 
   Промежуток [x_min,x_max] разбиваем на k=8 промежутков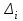 =(a_i-1,a_i] равной длины
   

h=R|k, i= 1,2, 3,... ,k согласно формуле 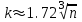. Здесь R= x_max - x_min.

h = 2,375.

3. 
   Находим частоты п_iпопадания элементов выборки в промежутки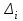 и средние точки z_i, промежутков.
   
4. 
   Составляем группированный статистический ряд оформленный в виде таблицы 2.
   

Группированный статистический ряд для выборки из табл. 1 Таблица 2.

№	Границы промежутков		пi	Средняя точка промежутка
1	17	19,375	8	18,1875
2	19,375	21,75	7	20,5625
3	21,75	24,125	26	22,9375
4	24,125	26,5	15	25,3125
5	26,5	28,875	14	27,6875
6	28,875	31,25	12	30,0625
7	31,25	33,625	8	32,4375
8	33,625	36	10	34,8125
			100

---

2. Графические характеристики выборки.

2.1 На основе таблицы 2 строим гистограмму и полигон приведенных частот с

вершинами в точках (z_{i ,} n _i | (nh)) (масштаб по оси Оу следует взять в 5-10 раз больше, чем по оси Ох). Гистограмму и полигон строим на одном рисунке под номером 1.



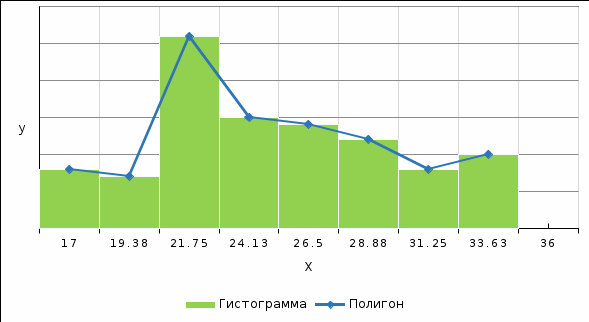
Рис. 1. Полигон и гистограмма частот

2.2 Строим график эмпирической функции распределения у = (x) со скачками n_i /n в
точках z_i , i=1, 2, 3, ...,k. График оформляем в виде рис.2.



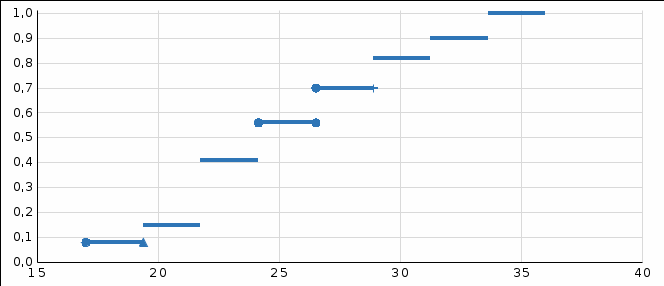
Рис. 2. Эмпирическая функция распределения

3. Выборочные числовые характеристики- оценки генеральных числовых
характеристик.

3.1 Находим приближенное среднее 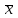и центральные выборочные моменты т₂, т₃, т₄

по формулам

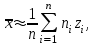
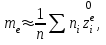(e=2, 3, 4), где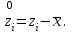

Вычисление моментов оформляется в виде таблицы 3.

Вычисление выборочных моментов Таблица 3.


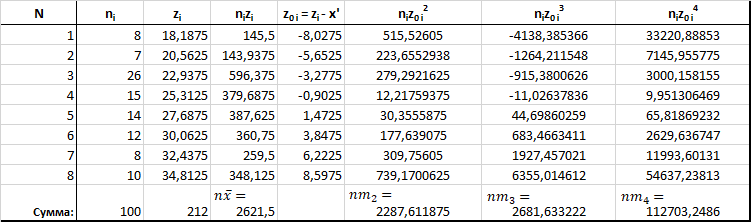
3.2 Вычисляем выборочные среднее квадратическое отклонение S, асимметрию а и эксцесс е по формулам

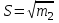, а = т₃/S³, e = (m₄/S⁴) - 3.

S = 4,78289857; а = 0,24509015; е = -0,84636674.

---

4. Сравнение выборочных графических характеристик с соответствующими теоретическими кривыми нормального распределения.

4.1 Для сравнения с гистограммой и полигоном приведенных частот на рис.1 строим график нормальной плотности вероятности

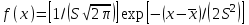по точкам 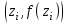, i=1, 2, 3, ...,k(рис.3 и рис.4 см. лекции)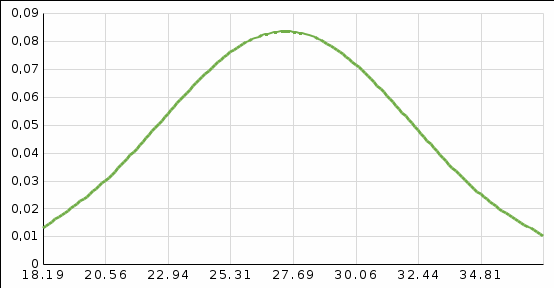



Рис. 3. Нормальное распределение плотности вероятности



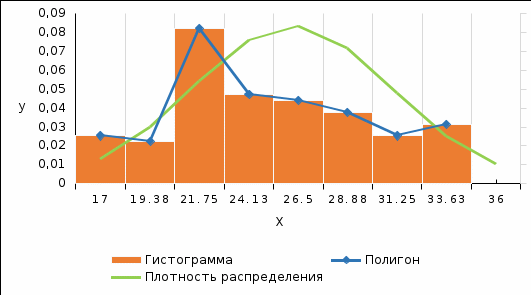
Рис. 4. Полигон и Гистограмма частот

4.2 Для сравнения с графиком эмпирической функции распределения у = (x) на рис.2 строим график функции распределения нормального закона N( ,S) по точкам (z_i,F(z_i)), где F(x) = 0.5 + Ф₀ [(х - )/S].

Ф₀(х) - нормированная функция Лапласа. Ее значения берем из таблицы II приложения.


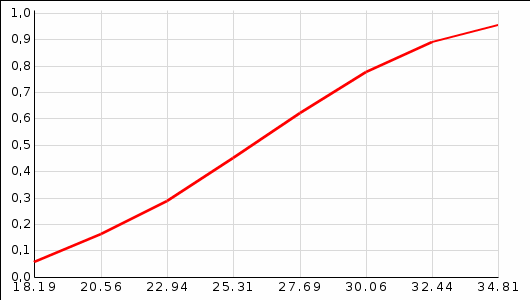
Рис. 5. Hормированная функция Лапласа



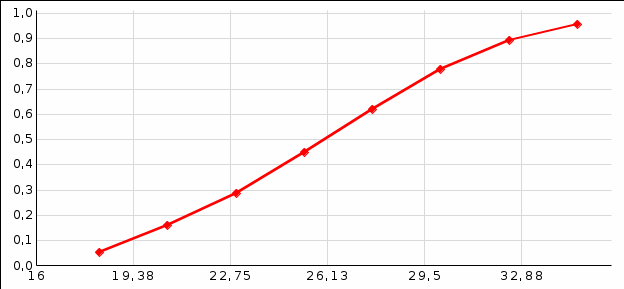
Рис. 6. Эмпирическая и теоретическая функция распределения

5. Анализ полученных результатов.

После сравнения гистограммы и графика эмпирической функции распределения с соответствующими теоретическими кривыми плотности и функции распределения выдвигаем гипотезу о нормальности генерального распределения.

---

6. Предварительная простейшая проверка гипотезы нормальности.

Выборочная асимметрия а и эксцесс е при гипотезе нормального генерального распределения должны быть близкими к нулю, но в силу случайности выборки их отличие от нуля может быть и значительным. Так как при n=100 совместно выполняются неравенства \а\ < -0.027 и |е| < -0.98 (что видно из пункта 3.2), то гипотеза нормальности может быть предварительно подтверждена с доверительной вероятностью 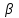= 0.95

---

Смотрите также файлы

• Отчет по учебной практике (лыжный сбор) Направление подготовки 44. 03. 01 педагогическое образование.odt

• Лекции по данной теме. Цель работы научиться обрабатывать текст в процессе решения задач.doc

• Исторические задачи Задача 1.docx

• Измерение амплитудночастотных характеристик.docx

• Ранние и поздние осложнения повреждений челюстнолицевой области.pptx