Аналогічно можна побудувати мультиплексори (рис. 5.16, а, б, в) відповідно до табл. 5.10.

Збільшення кількості джерел, що перемикають, і приймачів цифрової інформації досягається багатоступінчастим включенням мультиплексорів і демультиплексорів. Якщо виходи мультиплексоіов першого щабля підключити до входів мультиплексора другого щабля, утвориться так зване мультиплексорное дерево (рис. 5.17, а). Аналогічно будується демультиплексорное дерево (рис. 5.17, б).

Розглянемо деякі схемотехнічні застосування мультиплексорів. Можна використовувати мультиплексор як перетворювач паралельного -розрядного двійкового коду в послідовний. Для цього досить на входи мультиплексора подати паралельний код і потім послідовно' змінювати код адреси в необхідній послідовності. При цьому щоб уникнути появи помилкового сигналу на виході мультиплексора строб-імпульс на час перемикання адреси повинен відключати вихід від входів.

Аналогічно демультиплексор, виходи якого підключаються до входів запам'ятовувального регістра, можна використати для перетворення послідовного коду в паралельний.

Мультиплексори можна використовувати також для побудови логічних функцій декількох змінних у вигляді диз’юктивної нормальної форми. Нехай як приклад необхідно реалізувати логічну функцію

(5.7)

Дана логічна функція визначена тільки п'ятьма незалежними змінними. Якщо всі п'ять змінних подати на адресні входи відповідного мультиплексора, що має 2⁵=32 інформаційних входу, то для одержання на виході у будь-якої функції п'яти змінних досить подати «логічні I» на інформаційні входи, адреса яких збігається із мінтермами синтезованої функції. На інші входи аналогічно входу (рис. 5.18) необхідно подати

«логічні 0», виключивши тим самим відповідні комбінації з вихідної функції. Такий метод прийнятний, якщо функція т змінних містить близьке до 2^т кількість мінтермів. У противному випадку схема виходить надлишковою. Мультиплексор можна використати більш ефективно, якщо аргументи функції подавати не тільки на адресні, але й на інформаційні входи. Для цього, аргументи синтезованої функції розділяються на інформаційні входи і адресні входи так, щоб адресними входами управляли змінні, що найбільш часто входять у мінтерми функції. Алгоритм синтезу логічного пристрою на основі мультиплексора заключає у собі наступні операції: вихідна функція приводиться шляхом тотожних перетворень до СДНФ; для отриманої СДНФ будується карта Карно; на карті Карно виділяються області, елементи якої мають однакові адреси; для кожної адресної області визначається мінімальна форма відносно змінних, поданих на інформаційні входи; згідно отриманим мінімальним формам реалізується схема керування кожним інформаційним входом мультиплексора.

---

Проілюструємо алгоритм на розглянутому прикладі (5.7).

Доповнимо кожен мінтерм відсутніми аргументами:

Доповнюючи аналогічно кожен мінтерм, одержимо з виразу (5.7) СДНФ:

(5.8)

Для функції (5.8) побудуємо карту Карно, розподіливши для наочності адресні змінні по рядках і стовпцях (рис. 5.19, д).

На карті Карно виділені області D_o, D₁, D₂, D₃, що визначають функції керування відповідним інформаційним входом мультиплексора.

Мінімізуємо функції керування

(5.9)

Реалізуємо функції (5.9) на логічних елементах І, АБО, НЕ (рис. 5.19, б).

Якщо в розпорядженні користувача є 3-адресний мультиплексор, то для його восьми інформаційних входів карта Карно (рис. 5.20, а) розбивається на 8 областей D_o, ..., D₇, для яких одержуємо наступні функції керування:

Реалізація функції (5.7) на 3-адресному мультиплексорі (рис. 5.20, б) вимагає додатково лише один логічний елемент І.

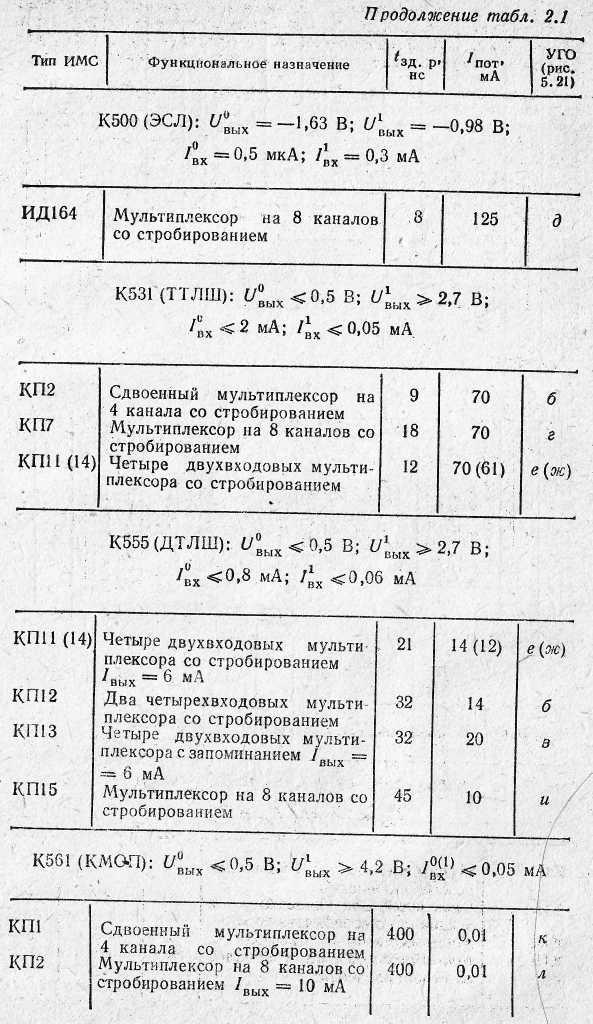
У табл. 5.11 наведені основні параметри найбільш широко застосовуваних мультиплексорів, демультиплексорів й аналогових комутаторів, а на рис. 5.21 - функціональне призначення виводів мікросхем.

5.3. КОМБІНАЦІЙНІ ПРИСТРОЇ ЗСУВУ.

Зсув цифрових даних необхідний при нормалізації чисел, при виконанні арифметичних операцій над ними й т.п. Якщо за один робочий такт потрібен зсув всього лише на один розряд уліво або вправо, то таку операцію, сполучивши її з функцією зберігання інформації, зручно виконувати за допомогою регістрів, що

зсувають, на тригерах. У випадку, коли за один такт виконується зсув на довільну кількість розрядів у будь-якому напрямку, зручніше скористатися комбінаційним логічним пристроєм на основі мультиплексорів. Кількість необхідних мультиплексорів дорівнює розрядності вихідного двійкового числа.

Вихідними даними для побудови пристрою, що зсуває, є таблиця, що встановлює зв'язок коду адреси мультиплексора з підключеним до кожного з його виходів розрядом числа, що зсуває. Розрядність адреси мультиплексора р визначає максимально можливий зсув числа за один такт

Нехай потрібно побудувати комбінаційний пристрій, що реалізує зсув згідно табл. 5.12. Для двухразрядної адреси максимальний зсув , тобто вхідне слово повинне містити розрядів. Звичайно для простоти керування на всі

мультиплексори подаються однакові коди адреси (хоча це обмеження не обов'язково). У комбінаційному пристрої зсуву (ШМАТ) (рис. 5.22, а) зсув числа виробляється вліво й при цьому старші розряди губляться. Для зсуву числа на розрядів без втрат старших розрядів необхідно додатковий пристрій, що зсуває (рис. 5.23), що забезпечує

Зсув числа згідно табл. 5.13. Даний варіант зсуваючого пристрою на основі мультиплексорної структури на рис. 5.22, б забезпечує зсув числа вліво, як показано в табл. 5.13, або вправо, якщо на адресні входи зсувача подати сигнали з інверсних виходів регістра (лічильника) адреси. При побудові арифметико-логічних пристроїв (АЛП), а також тактових генераторів і генераторів послідовностей імпульсів часто

---

необхідні кільцеві зсуваючі регістри, що забезпечують циркуляцію деякого числа й формування на виходах кільцевого регістра необхідних послідовностей імпульсів. Ці ж функції можна реалізувати комбінаційним кільцевим зсуваючим пристроєм, на вхід

якого подається двійкове число, що є операндом АЛП або програмує роботу тактового генератора. Як приклад приведемо схему 8-розрядного комбінаційного кільцевого зсувача (рис. 5.24), що реалізує таблицю істинності (табл. 5.14).

Крім високої швидкодії, обумовленої в основному часом спрацьовування дешифратора мультиплексора, комбінаційний пристрій зсуву забезпечує додаткові функціональні можливості: однокроковий зсув інформації в будь-якому напрямку на розрядів (); можливість перемикання вхідної інформації незалежно від установки коду адреси, тобто оперативної зміни операндів зсувача.

4. КОМБІНАЦІЙНІ СУМАТОРИ.

Суматор - пристрій, призначений для виконання операцій додавання й віднімання над багаторозрядними числами (операндами). Багаторозрядний суматор складається з

однорозрядних, реалізуючих додавання однорозрядних чисел. Однорозрядний суматор, на вхід якого надходять два однорозрядних числа й , а на виході формуються також однорозрядні числа суми і переносу , називають напівсуматором (рис. 5.25, а). Якщо однорозрядний суматор реалізує додавання трьох однорозрядних чисел , й (перенос із молодшого розряду), то такий суматор називають повним. У багаторозрядному суматорі тільки самий молодший розряд можна виконати за схемою напівсуматора, а інші розряди виконують функції повного суматора. Нижче розглянуті схеми суматорів для двійково кодованих чисел. Таблиця істинності для напівсуматора (табл. 5.15) дозволяє записати функцію обчислення суми і переносу одиниці переповнення у старший розряд:

(5.10)

Відповідно до виразу (5.10) напівсуматор можна реалізувати в базисі елементів І-НЕ (рис. 5.25, б), АБО-НЕ або на основі логічного елемента ВИКЛЮЧНЕ АБО й кон’юнктора (рис. 5.25, в). Можливі інші реалізації напівсуматора на підставі тотожних перетворень (5.10)

Відповідні реалізації показані на мал. 5.26, (а, б).

Вибір схеми для реалізації напівсуматора визначається наявної в розпорядженні розроблювача елементною базою з урахуванням вимог по швидкодії, енергоспоживанню й технологічності. Для забезпечення максимальної швидкодії переважніше схеми з мінімальною кількістю логічних щаблів між входом і виходом. Із цього погляду гадана простота напівсуматора на рис. 5.25, в не дає очікуваної переваги по швидкодії, тому що внутрішня структура ІМС ВИКЛЮЧНЕ АБО власне кажучи повторює фрагмент схеми на рис. 5.25, б.

Робота повного суматора описується табл. 5.16. Карта Карно для функцій й дає мінімальну форму і її тотожні варіанти:

---

(5.11)

(5.12)

Відповідно виразам (5.11), (5.12) на рис. 5.28 наведені різні реалізації повного суматора і його умовне графічне зображення. Схема суматора (рис. 5.28, в) аналогічна схемі на рис 5.28, б за структурою й параметрами, її можна побудувати на основі двох напівсуматорів (див. рис. 5.25, в). Суматор за схемою на рис. 5.28, а, що володіє мінімальною затримкою поширення сигналу й, відповідно, максимальною швидкодією, може з успіхом, застосовуватися при побудові ВІС багаторозрядного суматора. Варіант повного суматора на елементах І-АБО-НЕ, реалізований на ІМС промислових серій, показаний на рис. 5.28, д. Умовне графічне позначення однорозрядного суматора показане на рис. 5.28, д.

Аналогічно визначимо функції перемикання повного віднімача (називаного також субтрактором) - пристрою, що реалізує операцію віднімання двох однорозрядних чисел з формуванням сигналу позички зі старшого розряду. У відповідності з таблицею істинності віднімача (табл. 5.17), (рис 5.29) запишемо вирази для різниці і функції позички

(5.13)

(5.14)

Порівнюючи вирази для суми і переносу повного суматора з виразами для різниці і позички віднімача, бачимо, що вирази для й ідентичні, а для і - відрізняються. Якщо у вирази для і замість підставити , а замість - , то . Це означає, що віднімання можна замінити підсумовуванням, представивши від'ємник у зворотному коді з урахуванням необхідної інверсії функції позички. Це особливо важливо для побудови суматора, що виконує додавання чисел, з довільними знаками. Якщо ж необхідно робити операцію тільки віднімання, можна використати, одну зі схем на рис. 5.30. Схема на рис. 5.30, а виконує. операцію віднімання з мінімальною затримкою сигналу, у трьох логічних щаблях, але для її реалізації потрібно більше логічних елементів і з більшою кількістю входів. Схема, показана на рис. .5.3. б, виконана тільки на двовходових елементах І-НЕ, але має більшу затримку (6 логічних щаблів).

У цьому випадку формування значення різниці здійснюється відповідно до виразу (5.13), а позички - (5.14).

Сполучення операцій додавання й віднімання вимагає додаткового сигналу F, що встановлює режим роботи суматора. У суматорі (рис. 5.31) при F = 0

виробляється підсумовування чисел і формування переносу в наступний розряд, а при F = 1 - віднімання з і формування позички з старшого розряду.

Додавання багаторозрядних чисел можна реалізувати послідовно або паралельно. При послідовному підсумовуванні потрібно однорозрядний повний суматор, на вхід якого протягом тактового інтервалу послідовно, починаючи з молодшого розряду, подаються відповідні розряди доданків і результат переносу від додавання на попередньому такті (рис. 5.32, а). Результат підсумовування поразрядно з виходу суматора передається в лінію зв'язку або запам'ятовується в буферному регістрі, що зсуває, суми. Операція підсумовування закінчується через кількість тактів підсумовування

---

обумовлене розрядністю R_A, R_B чисел, що додаються А та В. Додатковий такт необхідний для реалізації переносу від підсумовування старших розрядів. Послідовний суматор вимагає мінімальних витрат устаткування, що не залежать від розрядності сумованих чисел. Однак тривалість операції підсумовування пропорційна розрядності операндів, тому послідовний суматор може використовуватися у відносно повільнодіючих цифрових пристроях.

В паралельному m-розрядному суматорі використається т повних суматорів (рис. 5.32, б), тобто витрати встаткування пропорційні розрядності операндів, але операція сумування виконується за один такт . Тривалість такту і складність реалізації паралельного суматора залежать від способу реалізації переносів. У найпростішому випадку виходи й входи ланцюгів переносу з'єднуються послідовно (рис. 5.32, б) і тривалість такту пропорційна кількості розрядів суматора й часу реалізації переносу в одному розряді

(5.15)

де - тривалість підсумовування в однорозрядному суматорі. При великій кількості розрядів і послідовної реалізації переносу тривалість підсумовування (5.15) виявляється неприпустимо великою. Збільшення швидкодії паралельного суматора досягається за рахунок одночасного формування сигналів переносу у всіх його т розрядах. Для цього в суматор включається спеціальна схема прискореного переносу, аргументами якої є проміжні змінні повного суматора.

Для побудови схеми паралельного переносу введемо позначення та перепишемо співвідношення (5.11) і (5.12) у вигляді

(5.16)

(5.17)

На підставі виразу (5.16) результат підсумовування на виходах багаторядного суматора:

(5.18).

де Р_о - можливий перенос при каскадному з'єднанні суматорів (для самої молодшої секції Р₀= 0), a P₁ .... Р_т визначаються виразом (5.17):

(5.19)

З виразу (5.19) видно, що схема паралельного переносу тим складніше, чим старше розряд суматора, але в будь-якому розряді тривалості операції переносу однакові й визначаються затримкою сигналу в чотирьох логічних щаблях (І, АБО): =4. Тоді сигнал суми, що запізнюється стосовно сигналу переносу, як видно з виразу (5.18), формується із затримкою .

Оскільки складність схеми паралельного переносу швидко наростає зі збільшенням номера розряду суматора, часто багаторозрядні суматори розбивають на секції, усередині яких реалізується паралельний перекіс, а між секціями перенос реалізується або послідовно, або по алгоритму, описуваному співвідношеннями виду (5.19).

На мал. 5.33, а показана схема 4-розрядного суматора з паралельним переносом. Перенос зі старшого розряду використається для передачі на вхід наступної секції (рис. 5.33, б), тобто між секціями перенос реалізується за послідовною схемою. У випадку великої кількості секцій між ними також можна реалізувати прискорений перенос.

---

Смотрите также файлы

• теорія по логічних елементах.doc

• Задачи ТДТ 2013.doc

• ТДТ Чепурний Задачник.pdf

• Характеристики газів.doc

• Діаграма пари.pdf