Перепишемо вираження для Р₄ з формул (5.19) для першої секції у вигляді

Тоді аналогічно перенос із другої секції:

і т.д.

Секції можна згрупувати по 4 і для 4 секцій (тобто 16 двійкових розрядів), формується груповий перенос.

Тоді структуру паралельного переносу між секціями можна виконати як на рис. 6.34. Прискорений перенос між розрядами 4-розрядних секцій також можна виконати по наведеній схемі. Якщо багаторозрядний суматор можна розділити на групи по 4 4-розрядні секції, то прискорений перенос між групами можна організувати аналогічно.

У мікрокалькуляторах, пристроях реєстрації й перетворення цифрової інформації, представленої в десятковій системі вирахування, широко використаються арифметичні пристрої із двоїчно-десятковим кодуванням операндів, з поданням десяткових чисел у коді + 3 («код з надлишком 3») або в коді Айкена (2421).

Рис. 5.34

Базовим елементом десяткового суматора є 4-розрядна секція двійкового суматора, що повинна реалізувати додавання двох десяткових цифр k-го розряду - і В_к4В_кзВ_к2В_к1 з урахуванням переносу , з тетради молодшого (k-1)-го десяткового розряду. На виходах k -й секції повинен бути отриманий результат суми S_k4S_k3S_k2S_kl і переноси Р_к у тетраду (k+1)-го десяткового розряду. Як видно з табл. 5.18, підсумовування двійково кодованих операндів дає суму і перенос які, починаючи з 10-й рядка, не відповідають підсумовуванню десяткових чисел. У рядках 16...19 потрібна корекція тільки суми, а в рядках 10...15 — і суми, і переносу. Корекція повинна перетворити суму у суму S_k4S_k3S_k2S_kl і перенос Р'_к у Р_к. Корекція переносу здійснюється логічним підсумовуванням Р_к=Р'_к+Р_кор, де Р_кор - коригувальний доданок, що приймає значення «логічної 1» на наборах S_k4S_k3S_k2S_k1 в 10...15 рядках табл. 5.18, т. е-

Таким чином, десятковий перенос визначається співвідношенням

Необхідність у корекції результату підсумовування виникає при Р_к = 1. При цьому для одержання правильного результату суми необхідно до проміжного результату додати код тобто використання двійкових суматорів для підсумовування двоїчно-десяткових чисел вимагає виконання підсумовування у два етапи:

Даний алгоритм реалізує схему для одного (рис. 5.35, а) і для m (рис. 5.35, б) десяткових розрядів. Застосування в ній двійкових суматорів із прискореним переносом дозволяє отримати швидкодіючий двоїчно-десятковий суматор.

Якщо яке-небудь одне або обоє доданків мають негативний знак, то операцію підсумовування чисел зі знаком можна замінити підсумовуванням чисел і знакових розрядів, причому модулі чисел, що мають негативний знак, представляють у

зворотному коді. Прийнято позначати позитивне число знаковим розрядом Z=0, тоді негативне число представляється значенням Z=1. Зворотний код десяткового числа отримується заміною кожної цифри (N) доповненням її до 9 (9-N) згідно табл. 5.1. Якщо при підсумовуванні знакових розрядів виникає перенос, то до молодшого розряду суми додається 1. Такий перенос називається циклічним і для його реалізації потрібен додатковий час. Якщо знак суми =0, то отримане на виходах суматора число є остаточним результатом (приклад 1). Якщо =1, то результат є негативним і його модулем представлений у зворотному коді. Остаточний результат виходить після

---

його модулем представлений у зворотному коді. Остаточний результат виходить після перетворення модуля на виходах суматора у зворотний код (9-) і присвоєння йому негативного знака (приклад 2).

Таким чином, якщо розглянуті вище двійково-десяткові суматори доповнити перетворювачами коду з N в «9-N» для модуля кожного доданка й модуля результату, а також замкнути ланцюг циклічного переносу, одержимо двоїчно-десятковий алгебраїчний суматор.

Відповідно до табл. 5.1 перетворювач коду 8421 у код ж9-JV» описується вираженнями

і реалізується схемою (рис. 5.36, а). Для цих же цілей можна використати 4-розрядний двійковий суматор у сполученні з елементами ВИКЛЮЧНЕ АБО (рис. 5.36, б). У цьому випадку при Z = 0 на виході суматора-перетворювача одержуємо число в коді 8421, а при Z = 1 - у коді «9- N». Використовуючи перетворювач коду (рис. 5.36, б), можна побудувати алгебраїчний суматор (рис. 5.37), у якому перетворення коду 8421 доданків в код «9- N» виробляється автоматично під керуванням власного знакового, розряду кожного з операндів. Аналогічно результат підсумовування в залежності від знака суми передається без зміни (Z_s = 0) або перетвориться з коду «9-N» у код 8421 за допомогою перетворювача коду (рис. 5.36, б). У багаторозрядному суматорі вихід переносу старшої декади необхідно підключити до входу переносу суматора знакових розрядів для організації циклічного переносу (рис. 5.38). Вихід переносу повного двійкового суматора знакових розрядів підключається до входу переносу самої молодшої декади. Варто звернути увагу на можливість одержання неправильного

результату з появою переносу з старшої декади суматора у зв'язку з переповненням розрядної сітки. Так, при додаванні двох позитивних чисел () результат також повинен бути позитивним, але при переповненні розрядної сітки виникає сигнал переносу й відповідно до вираження (5.11) формується Z_s = 1, що означає, що сума чисел має негативний знак. Користувачеві або пристрою керування цифровим автоматом необхідно передати сигнал про виникнення аварійної ситуації. Для цього формується сигнал позитивного переповнення

Аналогічно при додаванні двох негативних чисел результат повинен бути також негативним, а у випадку негативного переповнення результат виходить позитивним. Сигнал негативного переповнення визначається як

Тоді загальний сигнал переповнення визначається виразом

(5.20)

Схема, що реалізує функцію (5.20), може входити до складу ІМС суматора або повинна бути зібрана додатково.

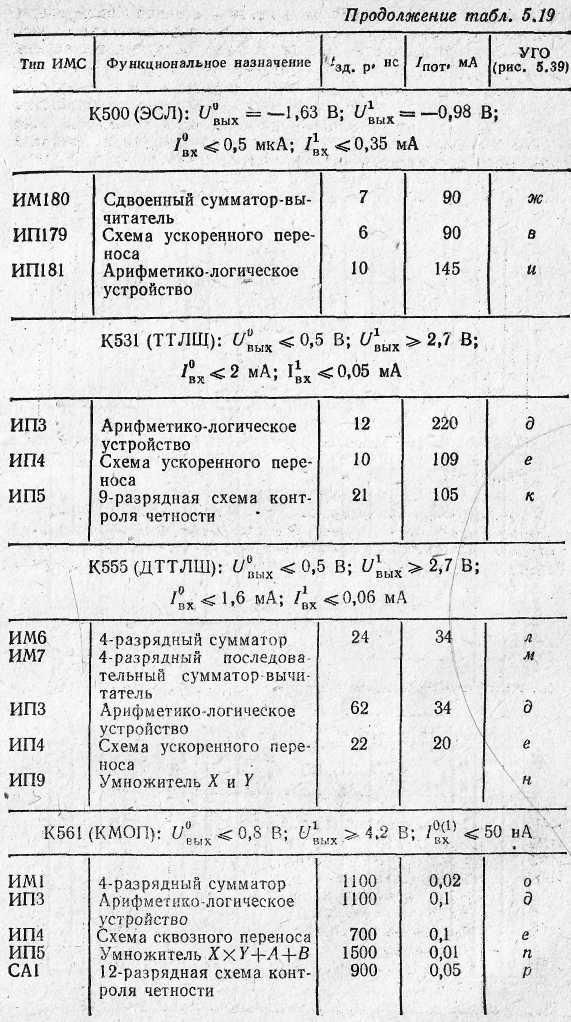
У табл. 5.19 наведені параметри суматора найбільш широко використовуваних серій ІМС, а на рис. 5.39 показане функціональне призначення виводів ІМС із табл. 5.19.

Комбінаційні суматори завдяки високій швидкодії застосовують у різних пристроях обробки цифрової інформації. Зокрема, на їхній основі будуються пристрої перемножування чисел. Для перемножування двох чисел А та В можна прості числа А скласти із самим собою В раз. Це можна виконати комбінаційними суматорами, але набагато швидше й економічніше пристрої підсумовування замінити підсумовуванням зі зсувом.

---

Як видно із приклада, власні добутки однозначно визначаються множеним і черговим бітом множника. Власний i-ий добуток або дорівнює множнику, якщо , або воно дорівнює нулю, якщо . Кожен наступний власний добуток зрушений на один розряд стосовно попереднього. Остаточний добуток виходить послідовним підсумовуванням власних добутків. Функціональна схема, що реалізує даний алгоритм на основі повних комбінаційних суматорів, показана на рис. 5.40. Операнди повних суматорів одержують за допомогою 2-входовых схем І аналогічно . .

Основне достоїнство комбінаційного помножувача - висока швидкодія (тривалість множення 8-разрядних двійкових чисел - менш 100 нс), що не зв'язано з тактовою

синхронізацією пристрою, а визначається лише затримками сигналів у логічних елементах. Висока швидкодія досягається ціною значних апаратурних витрат: для реалізації помножувача m-розрядного множеного і п-розрядного множника потрібно т*п логічних елементів 2І та п* (т -1) повних однорозрядних суматорів.

Комбінаційні помножувачі ефективно можна використати при побудові цифрових фільтрів, для виконання необхідних обчислень швидкого перетворення Фур'є, у мікропроцесорних системах.

---

Смотрите также файлы

• теорія по логічних елементах.doc

• Задачи ТДТ 2013.doc

• ТДТ Чепурний Задачник.pdf

• Характеристики газів.doc

• Діаграма пари.pdf