Файл: 2. Найти оценки неизвестных параметров распределения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 11
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Порядок выполнения работы
1. Для заданного статистического материала построить гистограмму и выдвинуть гипотезу о законе распределения генеральной совокупности.
2. Найти оценки неизвестных параметров распределения.
3. Проверить выдвинутую гипотезу по критерию
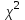на уровнях значимости 
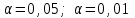.Ход работы:
Упорядочение выборки удобно сделать следующим образом: выписать все выборочные значения
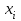; расположить в порядке возрастания выборочных значений. Наименьшее число равно 0.36240, наибольшее – 11,2085. Разделим интервал (0,36; 11,21) на 20 равных частей с шагом 0,5425. Разделенные интервалы представлены на рисунке 2.
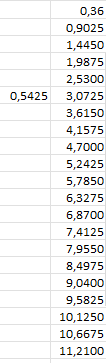
Рисунок 2 – разделенные интервалы.
Объединим интервалы так, чтобы новые интервалы содержали не менее 8 элементов. Новые границы интервалов, а также число элементов, попавших в уточненные интервалы, поместим в графы 4 и 5. В графу 6 поместим частоты попаданий в каждый интервал. Данный этап представлен на рисунке 3.
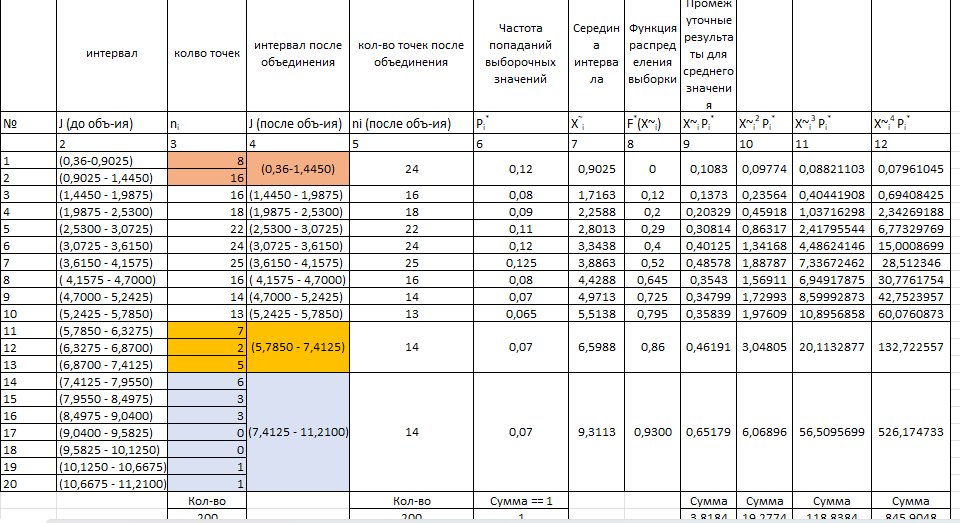
Рисунок 3 – заполненная таблица.
Построение графика эмпирической функции и гистограммы по полученным значением, представлены на рисунках 4, 5.
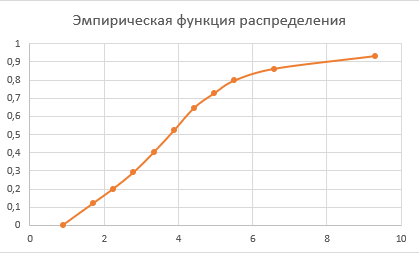
Рисунок 4 – эмпирическая функция распределения.
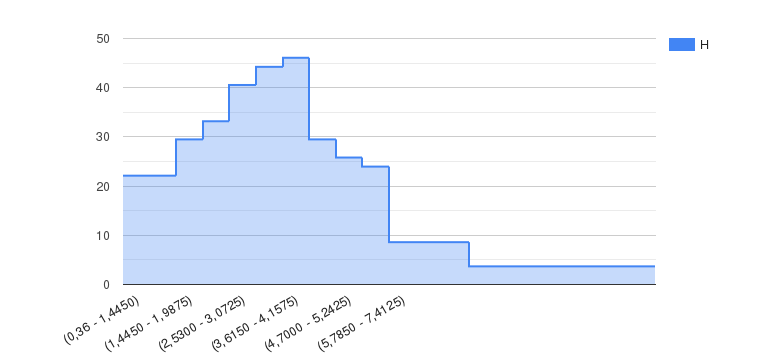
Рисунок 5 – Гистограмма
Вид гистограммы дает право выдвинуть гипотезу о показательном распределении генеральной совокупности.
Рассчитаем по нормальному закону
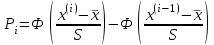, где
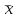- оценка математического ожидания, 
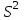- оценка дисперсии по выборке.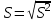 
- оценка среднего квадратичного;
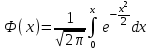- функция Лапласа (табл. А1). Смотрите на рисунок 6.
Рисунок 6 – рассчитанные значения Pi.
Значения функции Лапласа для интервалов представлены на рисунке 7.
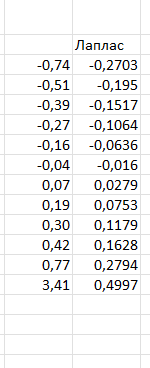
Рисунок 7 – значения функции Лапласа.
Оценка дисперсии при выборке представлена на рисунке 8.
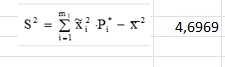
Рисунок 8 – оценка дисперсии при выборке.
Из большого числа различных критериев чаще других используется критерий согласия
, предложенный К. Пирсоном. В этом критерии в качестве меры расхождения теоретического и статистического распределений выбирается величина , определяемая равенством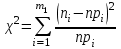
, (4)где n – объем выборки;
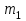– число интервалов, на которые разбита выборка; 
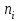–число элементов выборки, попавших в 
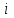-й интервал; 
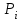– теоретическая вероятность попадания значений случайной величины в 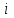-й интервал. Смотрите рисунок 9.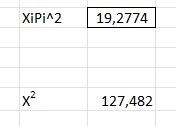
Рисунок 9 – Критерий согласия X^2
Случайная величина
, независимо от вида закона распределения генеральной совокупности, при достаточно больших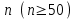 
имеет распределение с числом степеней свободы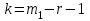 
, где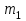
- число интервалов, r – число параметров распределения, определенных по выборке.
Задаваясь уровнем значимости
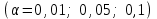, по таблице А2 определим критическое значение 
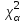, такое, что 
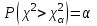. При больших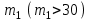 
распределено асимптотически нормально и можно пользоваться таблицами нормального закона. Если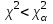 
, то выдвинутая гипотеза о виде закона распределения генеральной совокупности не отвергается на уровне значимости 
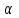(гипотеза не противоречит опытным данным), если же 
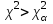, то гипотеза отвергается на уровне значимости 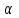. Смотрите рисунок 11.
Рисунок 11 – Определение критического значения X^2