Номер	x	y	x^2	y^2	x*y	y(x)
1	67174	142754	4512346276	20378704516	9589357196	142517,1043
2	677,4	1511	458870,76	2283121	1023551,4	1428,416302
3	603,3	1331	363970,89	1771561	802992,3	1271,195154
4	703,3	1473	494630,89	2169729	1035960,9	1483,369443
5	1057,2	2314	1117671,84	5354596	2446360,8	2234,25425
6	484,9	1100	235128,01	1210000	533390	1019,980797
7	477,5	1014	228006,25	1028196	484185	1004,279899
8	323,8	709	104846,44	502681	229574,2	678,1680179
9	594,3	1184	353192,49	1401856	703651,2	1252,099469
10	547,2	1181	299427,84	1394761	646243,2	1152,165379
11	2771,6	6628	7681766,56	43930384	18370164,8	5871,770254
12	412,2	834	169908,84	695556	343774,8	865,730089
13	520,4	1182	270816,16	1397124	615112,8	1095,302669
14	479,3	1006	229728,49	1012036	482175,8	1008,099037
15	507,6	1130	257657,76	1276900	573588	1068,14436
16	613,6	1407	376504,96	1979649	863335,2	1293,049106
17	779,6	1600	607776,16	2560000	1247360	1645,258425
18	668,8	1328	447293,44	1763584	888166,4	1410,169314
19	6242,9	10425	38973800,41	108680625	65082232,5	13236,97633
20	352,5	698	124256,25	487204	246045	739,0620387
21	475,4	985	226005,16	970225	468269	999,8242394
22	618,9	1291	383037,21	1666681	798999,9	1304,294344
23	610,4	1235	372588,16	1525225	753844	1286,259529
24	464,8	940	216039,04	883600	436912	977,3337648
25	743,4	1644	552643,56	2702736	1222149,6	1568,451333
26	445,8	864	198737,64	746496	385171,2	937,02065
27	310,5	665	96410,25	442225	206482,5	649,9488375
28	334,3	725	111756,49	525625	242367,5	700,4463182
29	2445,2	4581	5979003,04	20985561	11201461,2	5179,233376
30	153,3	443	23500,89	196249	67911,9	316,4108558
31	882	2641	777924	6974881	2329362	1862,524897
32	65,3	487	4264,09	237169	31801,1	129,6974819
33	309,7	894	95914,09	799236	276871,8	648,2514432
34	115,7	289	13386,49	83521	33437,3	236,6333233
35	164,5	431	27060,25	185761	70899,5	340,1743761
36	296	702	87616	492804	207792	619,1835656
37	2197,9	5096	4830764,41	25969216	11200498,4	4654,52636
38	1182,4	2710	1398069,76	7344100	3204304	2499,89646
39	449,9	994	202410,01	988036	447200,6	945,7197958
40	1256,2	2636	1578038,44	6948496	3311343,2	2656,481085
41	1903,6	4304	3623692,96	18524416	8193094,4	4030,097429
42	1846,2	4063	3408454,44	16507969	7501110,6	3908,309387
43	328,6	712	107977,96	506944	233963,2	688,3523837
44	396,6	857	157291,56	734449	339886,2	832,6309
45	1795,3	3762	3223102,09	14152644	6753918,6	3800,312675
46	766	1544	586756	2383936	1182704	1616,402722
47	598,3	1292	357962,89	1669264	773003,6	1260,58644
48	1333,8	2748	1779022,44	7551504	3665282,4	2821,128333
49	706,1	1443	498577,21	2082249	1018902,3	1489,310323
50	1755,1	3411	3080376,01	11634921	5986646,1	3715,018611
51	1044,2	2138	1090353,64	4571044	2232499,6	2206,671593
52	678,2	1408	459955,24	1982464	954905,6	1430,113697
53	1586,8	3189	2517934,24	10169721	5060305,2	3357,929283
54	1173,4	2608	1376867,56	6801664	3060227,2	2480,800774
55	606,3	1336	367599,69	1784896	810016,8	1277,560383
56	431,5	980	186192,25	960400	422870	906,6797267
57	2085	4410	4347225	19448100	9194850	4414,981589
58	1876,7	3323	3522002,89	11042329	6236274,1	3973,022545
59	1685,2	3531	2839899,04	12467961	5950441,2	3566,708783
60	87,7	204	7691,29	41616	17890,8	177,2245225
61	390,8	964	152724,64	929296	376731,2	820,3247912
62	104,8	309	10983,04	95481	32383,2	213,5063258
63	246,6	538	60811,56	289444	132670,8	514,3694671
64	1104,6	2543	1220141,16	6466849	2808997,8	2334,824863
65	183,6	1128	33708,96	1272384	207100,8	380,6996653
66	1427,8	2906	2038612,84	8444836	4149186,8	3020,572164
67	1129,5	2527	1275770,25	6385729	2854246,5	2387,656261
68	1313,1	2839	1724231,61	8059921	3727890,9	2777,208255
69	1229,8	2650	1512408,04	7022500	3258970	2600,467073
70	941,3	2035	886045,69	4141225	1915545,5	1988,34425
71	488,6	1034	238729,96	1069156	505212,4	1027,831245
72	483,3	950	233578,89	902500	459135	1016,586008
73	475,3	349	225910,09	121801	165879,7	999,6120651
74	979,1	2019	958636,81	4076361	1976802,9	2068,546131
75	726,7	1412	528092,89	1993744	1026100,4	1533,018227
76	425,7	881	181220,49	776161	375041,7	894,3736179
77	94,1	172	8854,81	29584	16185,2	190,803677
78	287,4	526	82598,76	276676	151172,4	600,9365768
79	81,6	187	6658,56	34969	15259,2	164,2818909
80	37,3	51	1391,29	2601	1902,3	70,28868104
Сумма	134348,6	284345	4627236744	20837681631	9816617346	284345
Среднее	1679,3575	3554,3125	57840459,3	260471020,4	122707716,8	3554,3125

---

Система нормальных уравнений.
an + b∑x = ∑y
a∑x + b∑x² = ∑yx

80a + 134348.6·b = 284345
134348.6·a + 4627236744.16·b = 9816617345.6
Домножим уравнение (1) системы на (-1679.358), получим систему, которую решим методом алгебраического сложения.
-134348.6a -225619396.199 b = -477517050.51
134348.6*a + 4627236744.16*b = 9816617345.6
Получаем:
4401617347.961*b = 9339100295.09
Откуда b = 2.1217
Теперь найдем коэффициент «a» из уравнения (1):
80a + 134348.6*b = 284345
80a + 134348.6*2.1217 = 284345
80a = -708.186
a = -8.8523
Получаем эмпирические коэффициенты регрессии: b = 2.1217, a = -8.8523
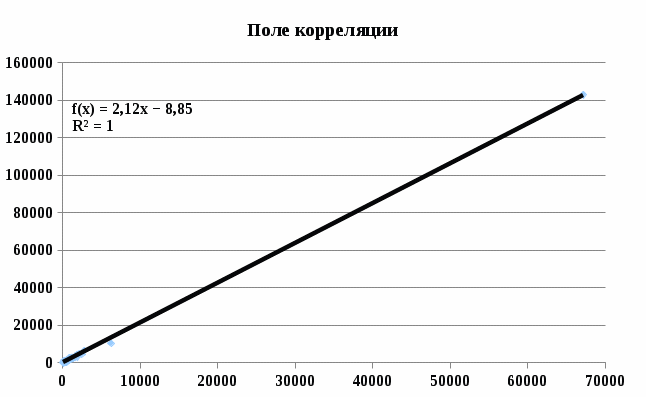
Уравнение регрессии:
y = 2.1217x -8.8523

Коэффициент регрессии b = 2.122 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 2.122.
Коэффициент a = -8.852 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Выборочные средние.



Выборочные дисперсии:



Коэффициент линейной парной корреляции:


Связь между признаком Y и фактором X весьма высокая и прямая.

R²= 0,9997² = 0.9994.

т.е. в 99.94% случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 0.06% изменения Y объясняются факторами, не учтенными в модели.

Коэффициент эластичности

---

:

Коэффициент эластичности находится по формуле:


В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%.

F-статистика. Критерий Фишера:




Табличное значение критерия со степенями свободы k₁=1 и k₂=78, F_табл = 3.92
Поскольку фактическое значение F > F_табл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна).

t-статистика. Критерий Стьюдента:
t_крит(n-m-1;α/2) = t_крит(78;0.025) = 2.284


Поскольку 360.99 > 2.284, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).


Поскольку 0.2 < 2.284, то статистическая значимость коэффициента регрессии a не подтверждается (принимаем гипотезу о равенстве нулю этого коэффициента). Это означает, что в данном случае коэффициентом a можно пренебречь.

Значимость коэффициента корреляции:

---

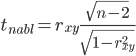
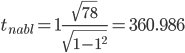
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=78 находим t_крит:
t_крит(n-m-1;α/2) = t_крит(78;0.025) = 2.284

Поскольку |t_набл| > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

---

Смотрите также файлы

• Электроэнергетика и электротехника.docx

• Социально культурный проект Школа искусств Актуальность. Какую проблему решает проект Отсутствие условий и площадок для реализации культурного и художественного .pptx

• Задание на курсовую работу по мдк 01. 01. Разработка нефтяных и газовых месторождений.docx

• Самостоятельная работа 1 Введение в предмет. История развития лыжного спорта.docx

• Рис. Схема хтс основными частями любой хтс являются элемент и подсистема.pdf