Файл: Методические указания по выполнению контрольных и расчетнографических работ Хабаровск Издательство двгупс 2017 удк 621. 317. 7(075. 8).doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 59
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КРИВЫХ НАПРЯЖЕНИЯ И ТОКА ЭЛЕКТРОВОЗА
1.1. Разложение функции на гармонические составляющие ряда Фурье
1.2. Порядок выполнения работы и содержание отчёта
2. ИССЛЕДОВАНИЕ РАБОТЫ ИЗМЕРИТЕЛЬНЫХПРЕОБРАЗОВАТЕЛЕЙ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
2.1. Описание работы измерительных преобразователей электрических величин
2.2. Порядок выполнения работы и содержание отчёта
2.3. Пример расчёта характеристик измерительного преобразования
;
3) график рассчитанных гармоник напряжения;
4) график основной функции напряжения, представляющий собой сумму всех гармоник;
5) расчёт синусиных и косинусных составляющих гармоник тока;
6) расчёт амплитуд и фаз гармоник тока;
7) график рассчитанных гармоник тока;
8) график основной функции тока, представляющий собой сумму всех гармоник.
Пусть в исходном задании представлены осциллограммы тока и напряжения (рис. 1.3, а). Для этих функций найдём параметры точек первого полупериода (рис.1.3, б) и запишем их в табл. 1.2.
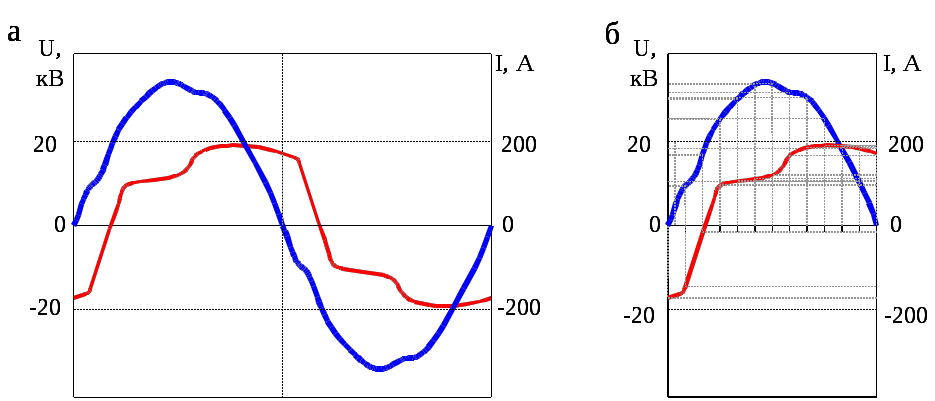
Рис. 1.3. Пример задания на работу (а) и определение координат точек
в кривых напряжения и тока (б)
Таблица 1.2
Параметры точек для примера задания
В этом примере определим только параметры кривой тока, поскольку она наиболее искажена, соответственно имеет большие амплитуды гармоник. При выполнении работы необходимо определить как параметры кривой тока, так и параметры кривой напряжения.
По найденным точкам находим синусные и косинусные составляющие кривой тока по формулам (1.6) для каждой гармоники:
– для первой гармоники
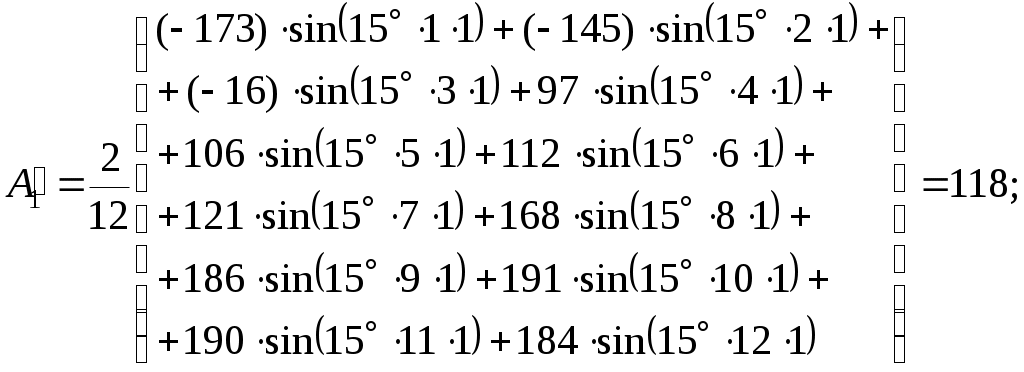
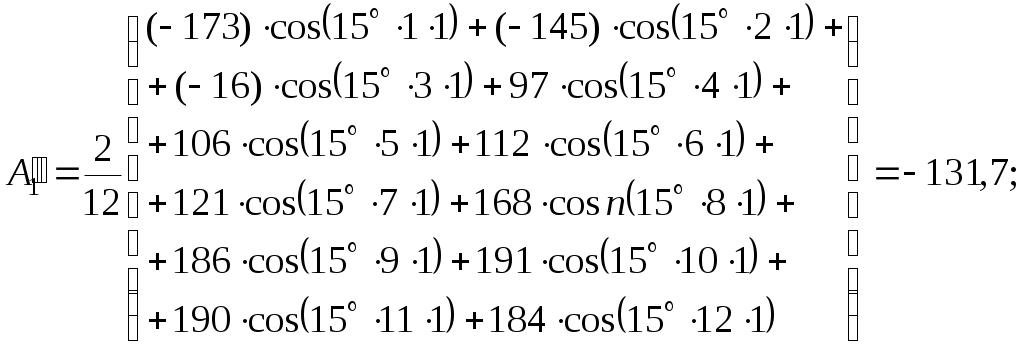
– для третьей гармоники
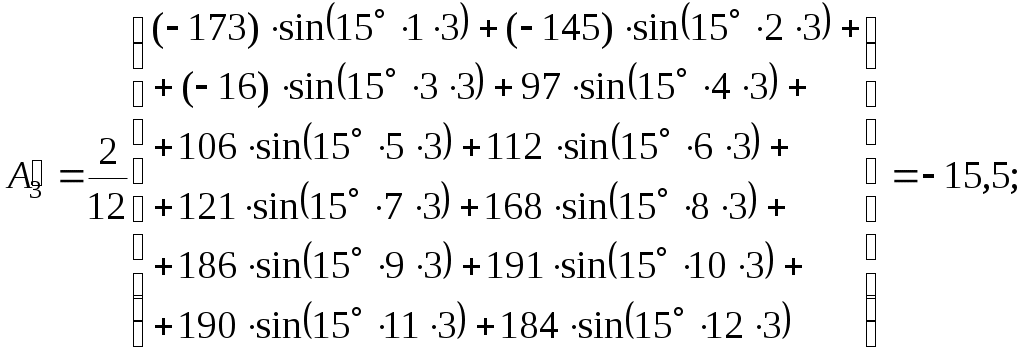
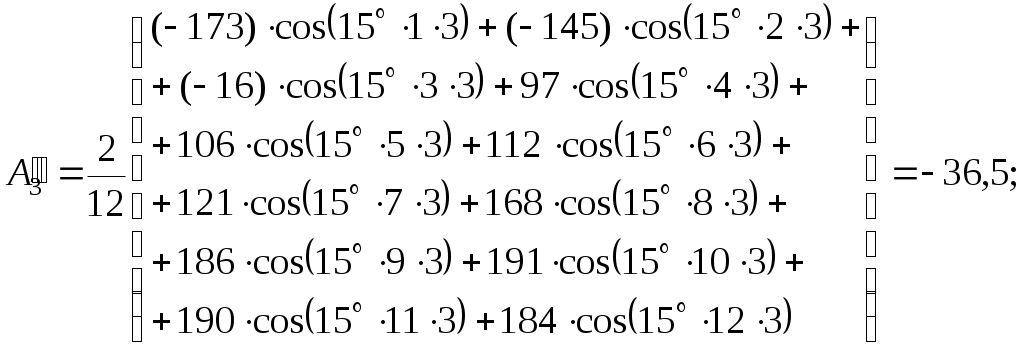
– для пятой гармоники
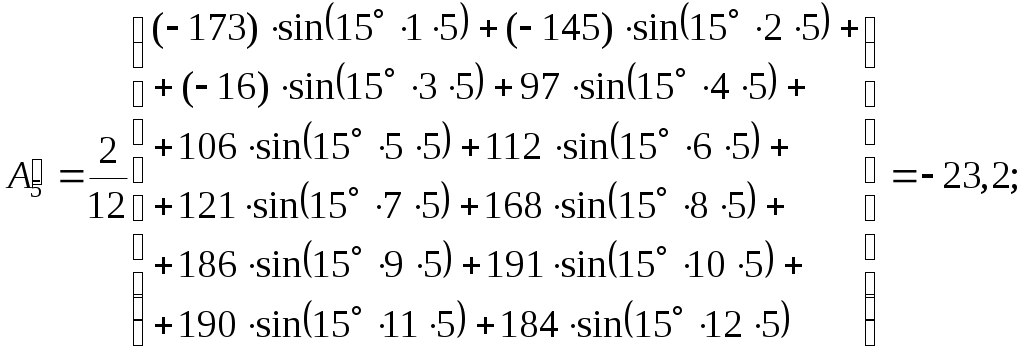
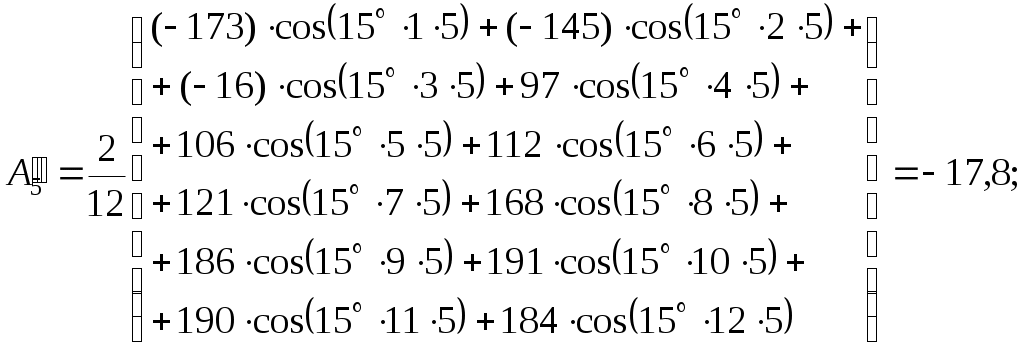
– для седьмой гармоники
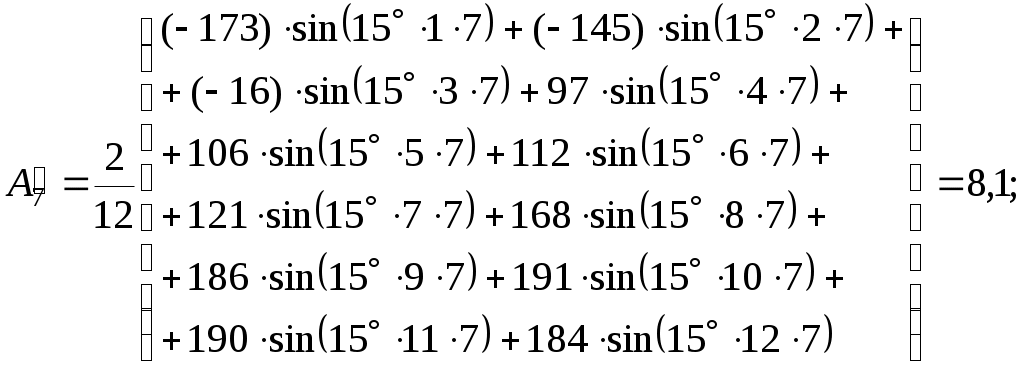
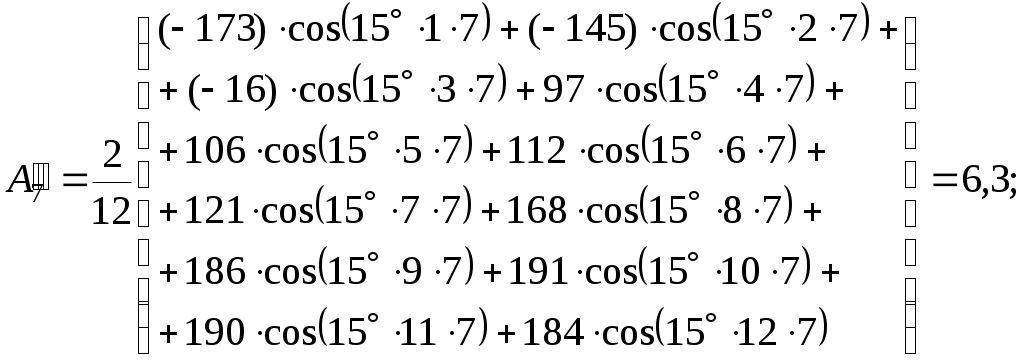
– для девятой гармоники
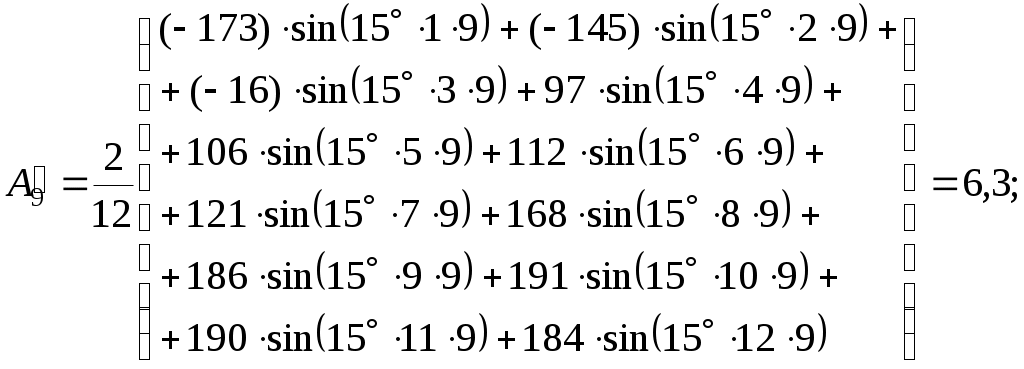
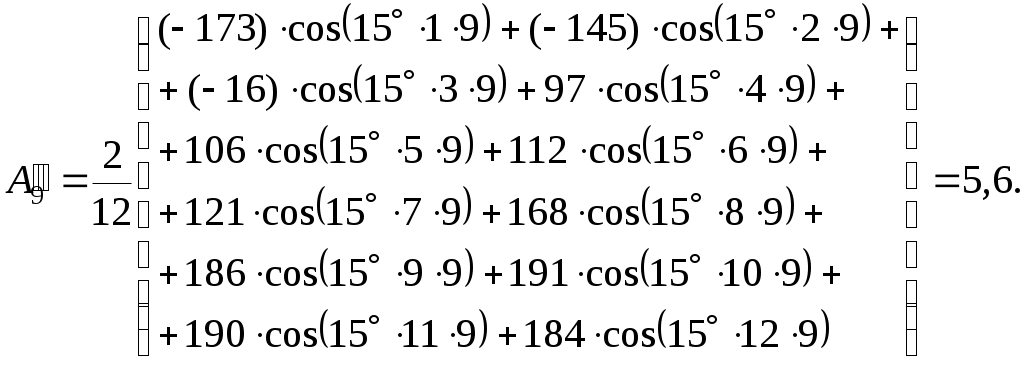
С применением полученных значений находим по формулам (1.3) и (1.4) амплитуды и углы каждой гармоники:
– для первой гармоники
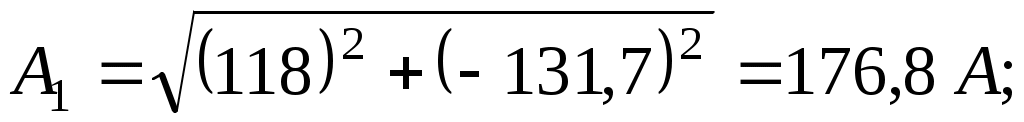
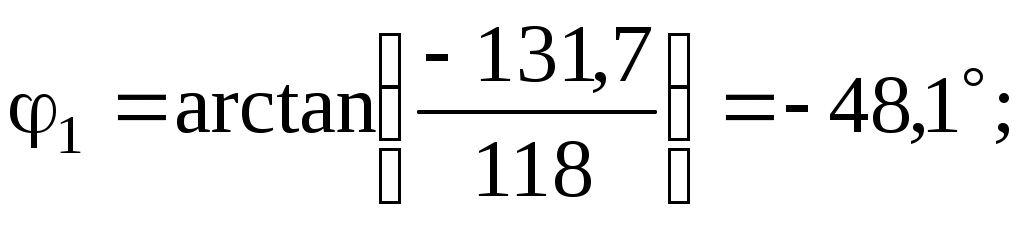
– для третьей гармоники
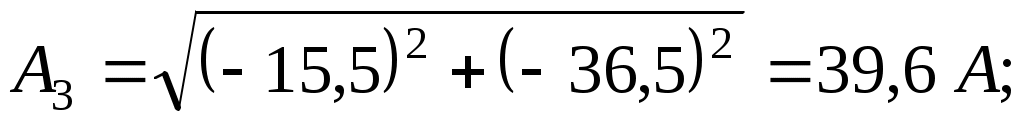
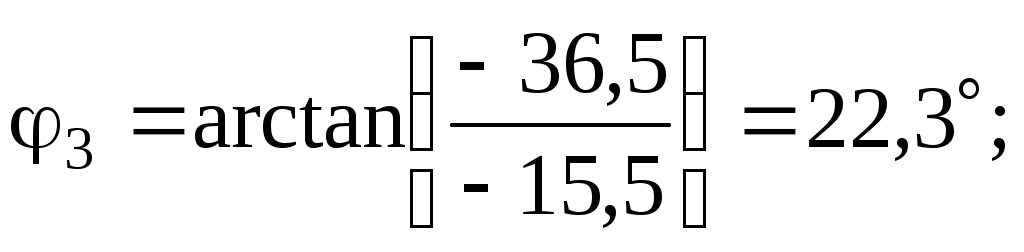
– для пятой гармоники
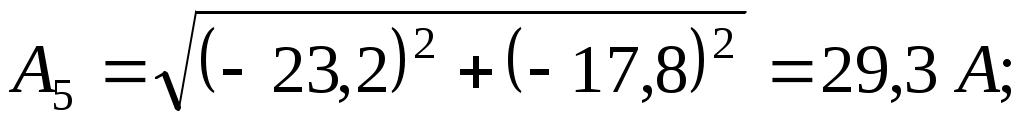
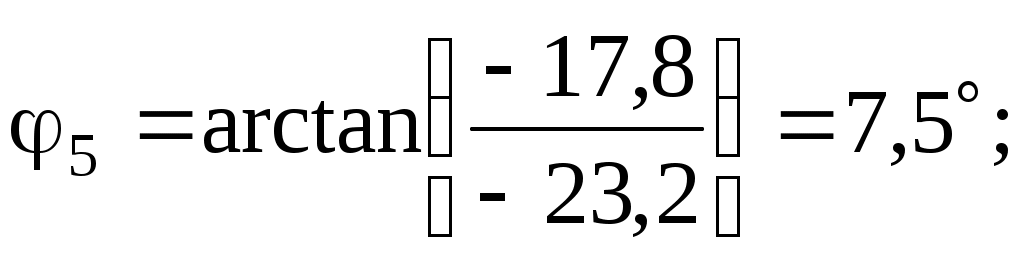
– для седьмой гармоники
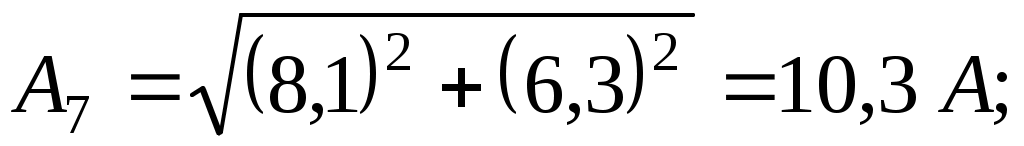
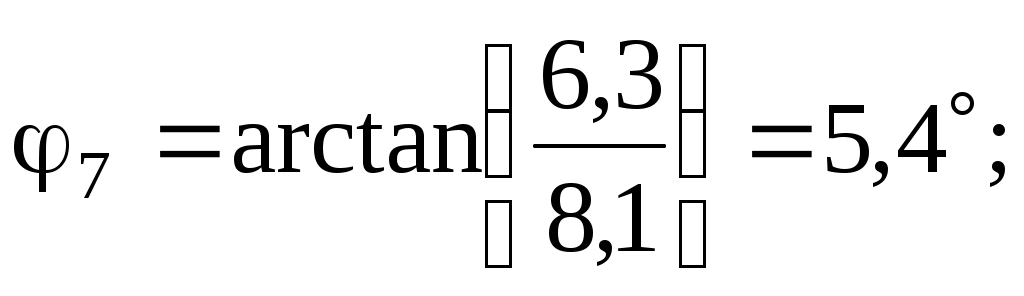
– для девятой гармоники
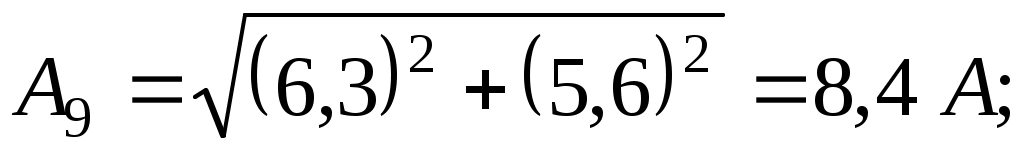
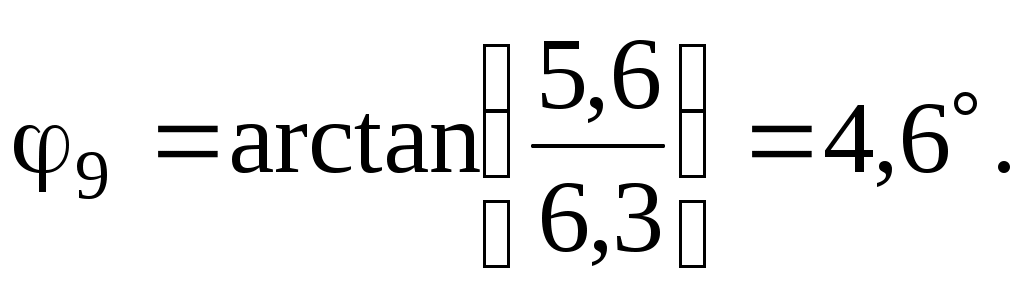
По полученным параметрам построим график со всеми гармониками (рис. 1.4) и график суммы всех гармоник (рис. 1.5).
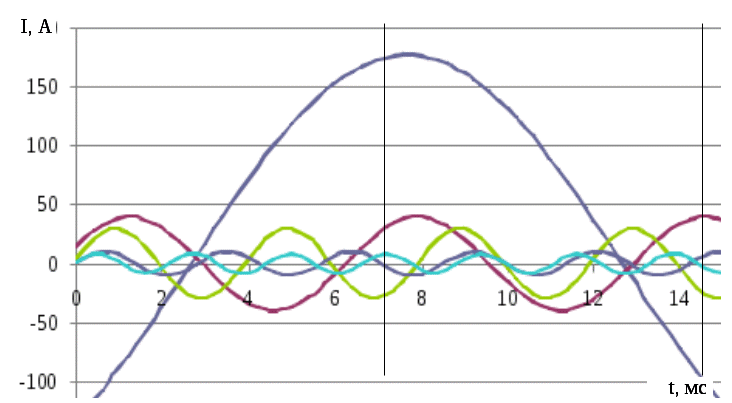
Рис. 1.4. График всех рассчитанных гармоник
Полученный график отдалённо напоминает исходный график кривой тока. Это объясняется тем, что при расчётах функция разбивается на малое число отрезков, а число гармоник ограниченно первыми пятью. При разбиении функции на большее число отрезков и с учётом большего числа гармоник, итоговый график по форме будет приближен к исходному.
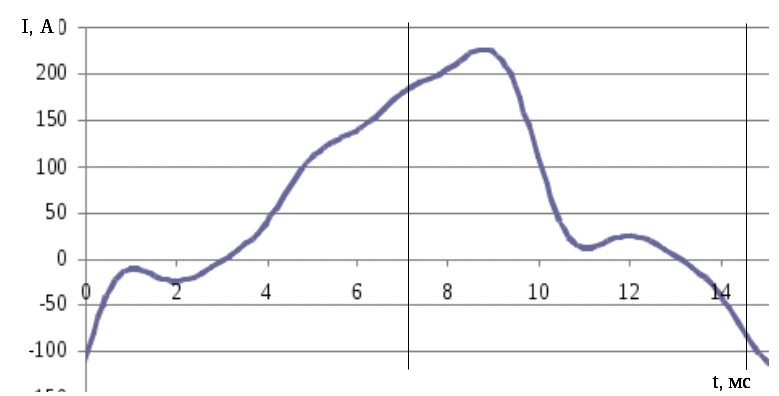
Рис. 1.5. График суммы рассчитанных гармоник
Расчёт параметров кривой напряжения производится аналогично приведённому выше расчёту параметров кривой тока. После расчёта этих параметров необходимо также построить графики гармоник, аналогичные представленным на рис. 1.4–1.5.
2. ИССЛЕДОВАНИЕ РАБОТЫ ИЗМЕРИТЕЛЬНЫХ
2.1. Описание работы измерительных преобразователей
Измерительный преобразователь (ИП) – это устройство, предназначенное для преобразования входной физической величины в другую, удобную для измерения физическую величину. Одним из видов таких ИП является преобразователь электрических величин (ИПЭВ), который входную электрическую величину преобразует в другую электрическую величину на выходе, или изменяет её параметры заданным образом.
В настоящей работе рассматриваются ИПЭВ, на вход которого подаётся переменное напряжения, а с выхода снимается унифицированный сигнал постоянного тока. Примером такого преобразователя является преобразователь типа Е842, который осуществляет линейное преобразование входного сигнала переменного тока в унифицированный сигнал постоянного тока. Такие преобразователи применяются для контроля тока и напряжения в различных электрических устройствах и установках. Для питания таких преобразователей используется отдельный источник питания. Схема для проведения измерения с использованием ИПЭВ показана на рис. 2.1.
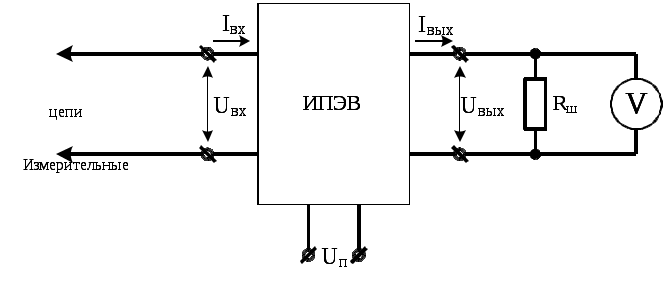
Рис. 2.1. Схема включения измерительного преобразователя электрических величин
Если функция преобразователя известна, то по значению входной величины можно найти выходную. Однако, изменение параметров преобразователя вследствие различных причин, может привести к тому, что выходная величина не будет строго соответствовать заданной функции от входной (появление погрешностей измерения). Для обнаружения таких несоответствий необходимо проводить измерения входных и выходных величин высокоточными приборами.
Рассмотрим процесс изменения характеристик ИПЭВ. На рис. 2.2 представлена идеальная (действительная) yд = fд(x) и реальная
y = f(x) функции преобразования. Реальная функция – это функция, учитывающая несоответствие заданной функции вследствие появления погрешностей измерения.
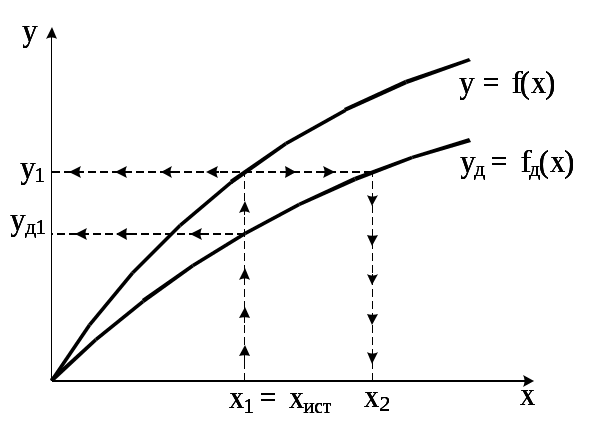
Рис. 2.2. Идеальная (действительная) и реальная характеристики измерительного преобразователя
В случае наличия погрешностей измерения, при подаче на вход измеряемой величины х1 на выходе получим результат у1 = f(x1), а не значение у1д = fд(x1), которое должно было получиться при отсутствии погрешностей (идеальный случай). Разность между полученным и ожидаемым результатом выходной величины есть абсолютная погрешность измерения по выходу
Δy=|у1– у1д|.(2.1)
Если на выходе ИПЭВ наблюдается величина у1, то в идеальном случае это должно означать, что на входе имеется величина x2 (рис. 2.1). Однако из-за наличия погрешностей появление на выходе величины у1 создаёт подача на вход другой величины x1 =xист. Разность между полученным результатом измеряемой величины x2и его истинным значениемxист есть абсолютная погрешность измерения по входу
Δx= |x2– x1|.(2.2)
Абсолютная погрешность может выражаться в крайне малых или больших значениях, неудобных для анализа. По этой причине используется относительная погрешность, определяемая отношением абсолютной погрешности измерения к измеряемой величине, которая выражается в процентах
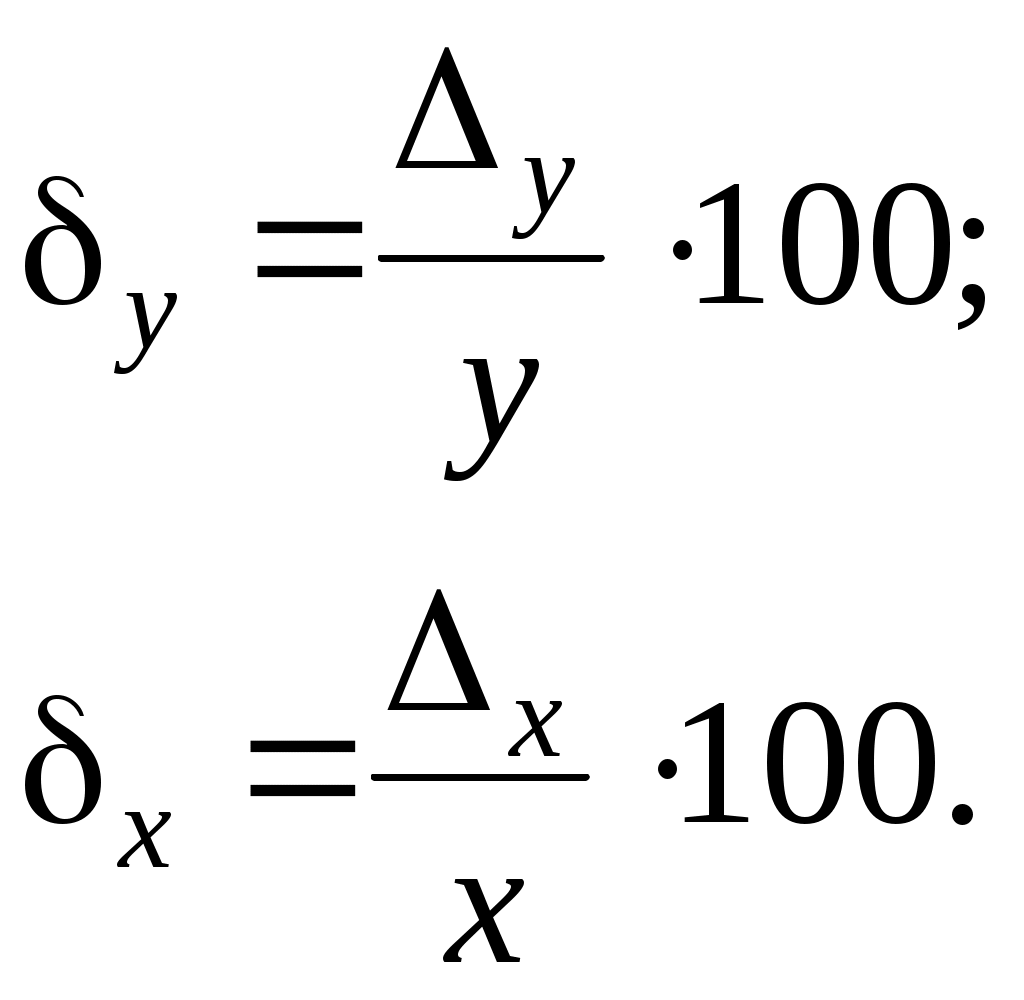 (2.3)
(2.3)
В формулах (2.3) в знаменатель необходимо подставлять значения из исходных данных (измеренная величина).
Действительные значения можно найти используя действительный коэффициент преобразования Кд при условии, что он неизменен во всём диапазоне измерения (линейная функция преобразования). В этом случае используется
3) график рассчитанных гармоник напряжения;
4) график основной функции напряжения, представляющий собой сумму всех гармоник;
5) расчёт синусиных и косинусных составляющих гармоник тока;
6) расчёт амплитуд и фаз гармоник тока;
7) график рассчитанных гармоник тока;
8) график основной функции тока, представляющий собой сумму всех гармоник.
1.3. Пример выполнения работы
Пусть в исходном задании представлены осциллограммы тока и напряжения (рис. 1.3, а). Для этих функций найдём параметры точек первого полупериода (рис.1.3, б) и запишем их в табл. 1.2.

Рис. 1.3. Пример задания на работу (а) и определение координат точек
в кривых напряжения и тока (б)
Таблица 1.2
Параметры точек для примера задания
| № точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| t, мс | 0 | 0,833 | 1,667 | 2,500 | 3,333 | 4,167 | 5,000 | 5,833 | 6,667 | 7,500 | 8,333 | 9,167 | 10 |
| U, кВ | 0 | 9,46 | 16,85 | 25,41 | 30,22 | 33,60 | 33,96 | 31,89 | 30,74 | 25,53 | 18,40 | 10,49 | 0 |
| I, А | -173 | -145 | -16 | 97 | 106 | 112 | 121 | 168 | 186 | 191 | 190 | 184 | 173 |
В этом примере определим только параметры кривой тока, поскольку она наиболее искажена, соответственно имеет большие амплитуды гармоник. При выполнении работы необходимо определить как параметры кривой тока, так и параметры кривой напряжения.
По найденным точкам находим синусные и косинусные составляющие кривой тока по формулам (1.6) для каждой гармоники:
– для первой гармоники
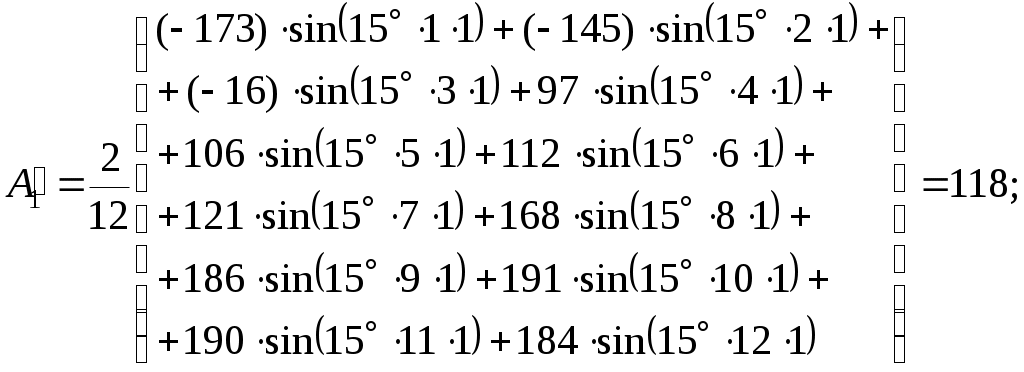
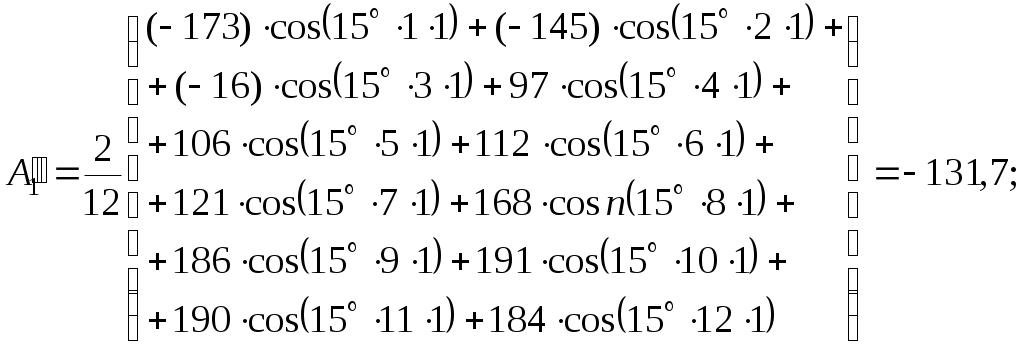
– для третьей гармоники
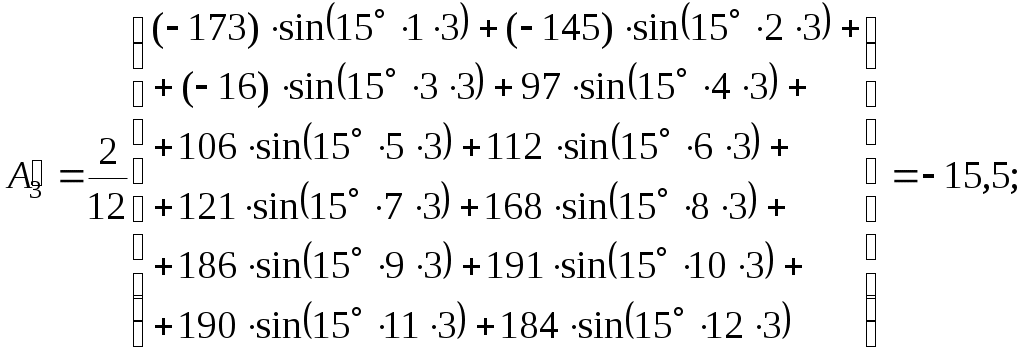
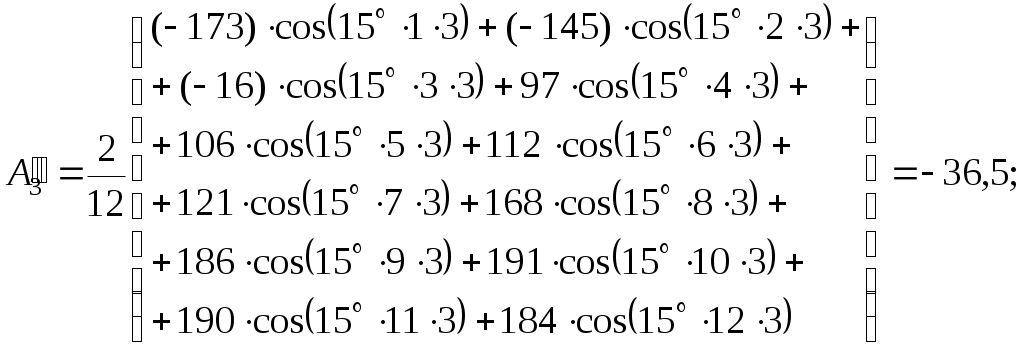
– для пятой гармоники
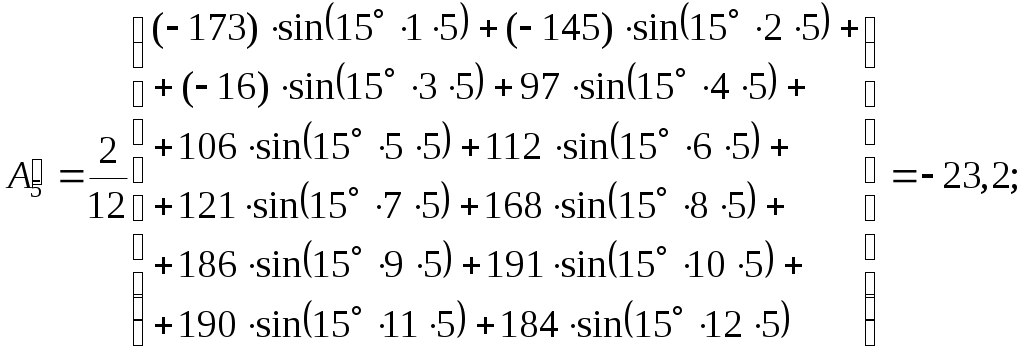
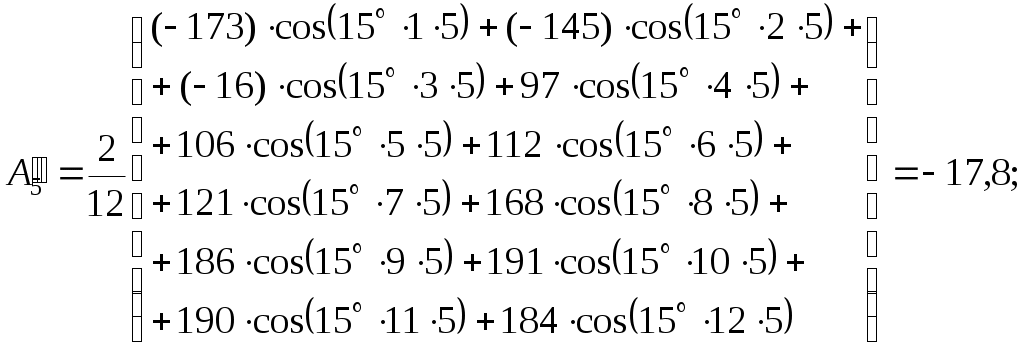
– для седьмой гармоники
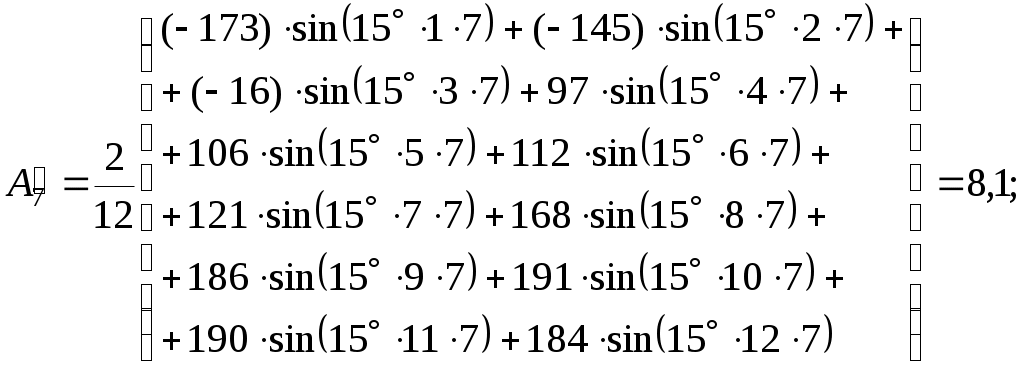
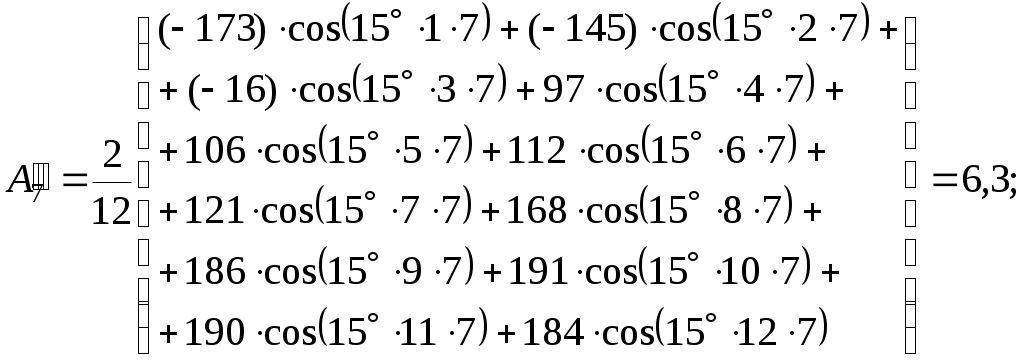
– для девятой гармоники
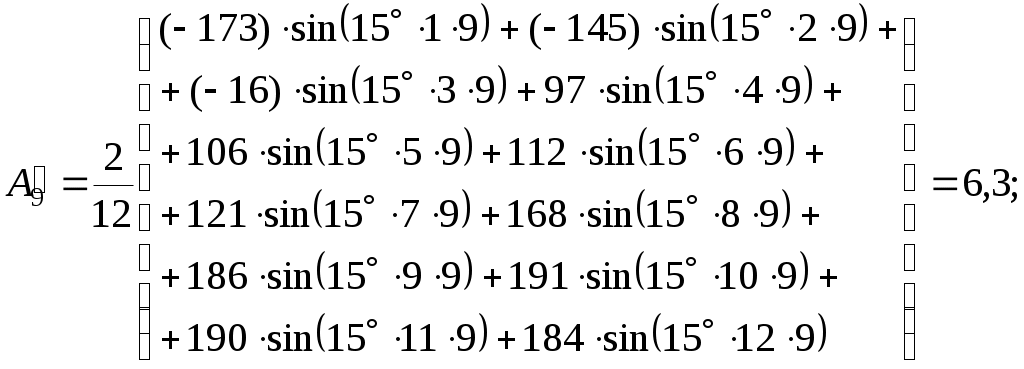
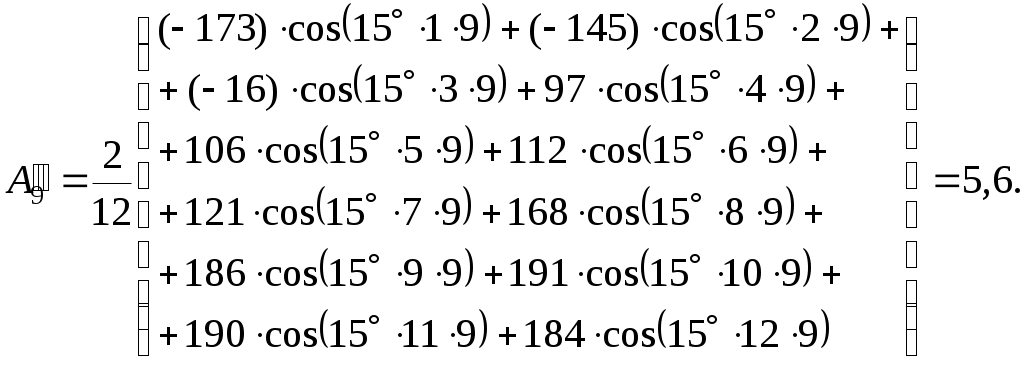
С применением полученных значений находим по формулам (1.3) и (1.4) амплитуды и углы каждой гармоники:
– для первой гармоники
– для третьей гармоники
– для пятой гармоники
– для седьмой гармоники
– для девятой гармоники
По полученным параметрам построим график со всеми гармониками (рис. 1.4) и график суммы всех гармоник (рис. 1.5).

Рис. 1.4. График всех рассчитанных гармоник
Полученный график отдалённо напоминает исходный график кривой тока. Это объясняется тем, что при расчётах функция разбивается на малое число отрезков, а число гармоник ограниченно первыми пятью. При разбиении функции на большее число отрезков и с учётом большего числа гармоник, итоговый график по форме будет приближен к исходному.

Рис. 1.5. График суммы рассчитанных гармоник
Расчёт параметров кривой напряжения производится аналогично приведённому выше расчёту параметров кривой тока. После расчёта этих параметров необходимо также построить графики гармоник, аналогичные представленным на рис. 1.4–1.5.
2. ИССЛЕДОВАНИЕ РАБОТЫ ИЗМЕРИТЕЛЬНЫХ
ПРЕОБРАЗОВАТЕЛЕЙ ЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН
2.1. Описание работы измерительных преобразователей
электрических величин
Измерительный преобразователь (ИП) – это устройство, предназначенное для преобразования входной физической величины в другую, удобную для измерения физическую величину. Одним из видов таких ИП является преобразователь электрических величин (ИПЭВ), который входную электрическую величину преобразует в другую электрическую величину на выходе, или изменяет её параметры заданным образом.
В настоящей работе рассматриваются ИПЭВ, на вход которого подаётся переменное напряжения, а с выхода снимается унифицированный сигнал постоянного тока. Примером такого преобразователя является преобразователь типа Е842, который осуществляет линейное преобразование входного сигнала переменного тока в унифицированный сигнал постоянного тока. Такие преобразователи применяются для контроля тока и напряжения в различных электрических устройствах и установках. Для питания таких преобразователей используется отдельный источник питания. Схема для проведения измерения с использованием ИПЭВ показана на рис. 2.1.

Рис. 2.1. Схема включения измерительного преобразователя электрических величин
Если функция преобразователя известна, то по значению входной величины можно найти выходную. Однако, изменение параметров преобразователя вследствие различных причин, может привести к тому, что выходная величина не будет строго соответствовать заданной функции от входной (появление погрешностей измерения). Для обнаружения таких несоответствий необходимо проводить измерения входных и выходных величин высокоточными приборами.
Рассмотрим процесс изменения характеристик ИПЭВ. На рис. 2.2 представлена идеальная (действительная) yд = fд(x) и реальная
y = f(x) функции преобразования. Реальная функция – это функция, учитывающая несоответствие заданной функции вследствие появления погрешностей измерения.

Рис. 2.2. Идеальная (действительная) и реальная характеристики измерительного преобразователя
В случае наличия погрешностей измерения, при подаче на вход измеряемой величины х1 на выходе получим результат у1 = f(x1), а не значение у1д = fд(x1), которое должно было получиться при отсутствии погрешностей (идеальный случай). Разность между полученным и ожидаемым результатом выходной величины есть абсолютная погрешность измерения по выходу
Δy=|у1– у1д|.(2.1)
Если на выходе ИПЭВ наблюдается величина у1, то в идеальном случае это должно означать, что на входе имеется величина x2 (рис. 2.1). Однако из-за наличия погрешностей появление на выходе величины у1 создаёт подача на вход другой величины x1 =xист. Разность между полученным результатом измеряемой величины x2и его истинным значениемxист есть абсолютная погрешность измерения по входу
Δx= |x2– x1|.(2.2)
Абсолютная погрешность может выражаться в крайне малых или больших значениях, неудобных для анализа. По этой причине используется относительная погрешность, определяемая отношением абсолютной погрешности измерения к измеряемой величине, которая выражается в процентах
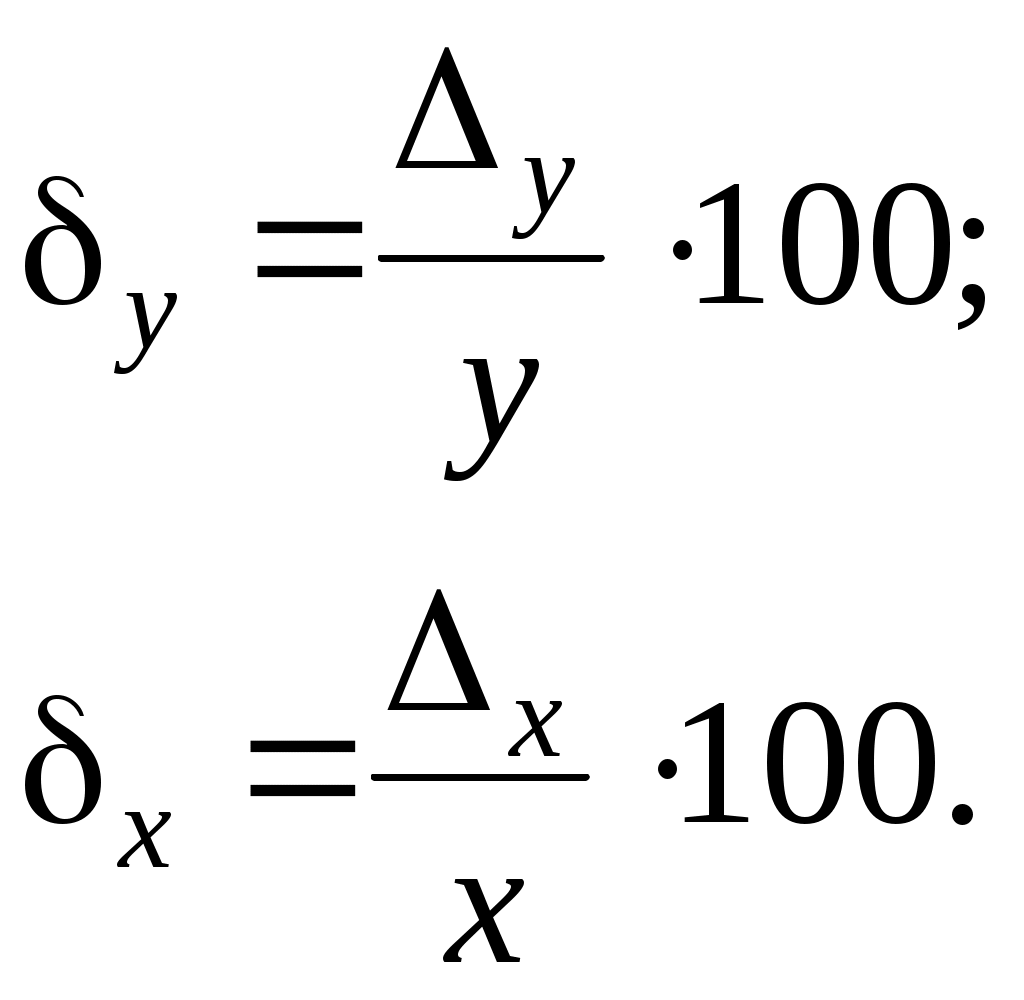 (2.3)
(2.3)В формулах (2.3) в знаменатель необходимо подставлять значения из исходных данных (измеренная величина).
Действительные значения можно найти используя действительный коэффициент преобразования Кд при условии, что он неизменен во всём диапазоне измерения (линейная функция преобразования). В этом случае используется