Файл: Отче т.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 325

Скачиваний: 12

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



У Г Т У - У П И

Кафедра физики



О Т Ч Е Т


по лабораторной работе № 10

Изучение распределения Максвелла

Студент: Пятков Юрий Станиславович

Группа: СТВ-120025ду

Дата: 15.01.2023

Преподаватель: Леменкова Вера Владимировна

1. Объект исследования - электронный газ, находящийся в состоянии термодинамического равновесия при Т Ткатода в электронной лампе.

2. Расчетные формулы:

2.1. Наиболее вероятная скорость VB электронов:



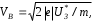
где 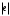- модуль заряда электрона; 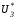- задерживающее напряжение, соответствующее максимуму на кривой зависимости I от U3.

2.2. Абсолютная температура Т электронного газа

.

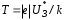3. Обработка результатов наблюдений:

3.1. Построить график экспериментальной зависимости IотU3. Соответствующие значения U3 и I перенести с экрана дисплея в таблицу (выбрать не менее 15 точек вблизи точки перегиба).

Таблица

U3, В
0,09
0,12
0,15
0,18
0,21
0,24
0,27
0,30

I ,мкА/В
230,2
220,4
209,7
198,3
186,2
173,7
161,1
148,3

dI / dU
78,212
87,536
92,873
95,35
95,733
94,577
92,3
89,21


3.2. Значение 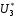, соответствующее максимуму I,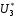

= 0,21 B.

3.3. Расчет наиболее вероятной радиальной скорости VrB электронов

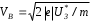
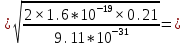2,846×1020 м/с.
3.4. Расчет абсолютной температуры T электронного газа

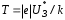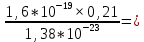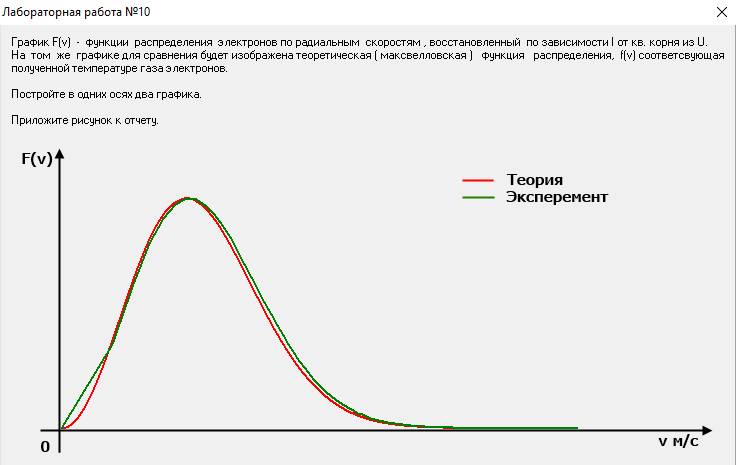
= 2434,78 К.

3.5. Списать таблицу и построить графики зависимости функции Максвелла F(v) – теоретической и экспериментальной - от скорости V электронов в электронном газе (выбрать 10-15 точек – по 5-7 слева и справа от максимума).

Константы:

  1. модуль заряда электрона e= 1,6010-19 Кл;

  1. масса электрона m = 9,1110-31 кг;

  2. постоянная Больцмана k = 1,3810-23 Дж/К.


4. Выводы:

В ходе лабораторной работы мы выяснили, что частицы газа движутся хаотично, поэтому все направления вектора скорости частиц равномерны, а величина скорости принимает различные значения.

Графики кривых построены путем подстановки мнимых чисел из кода программы, в результате чего расхождения по графикам минимальны. Таким образом, можно сказать, что функция распределения Максвелла хорошо описывает состояние электронного газа по скоростям.

Смотрите также файлы