Файл: Задания на летние каникулы после 6 класса Выполнить действия целыми числами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задания на летние каникулы после 6 класса
1.Выполнить действия целыми числами:
| а) -6-3 б) 3-4 в) 2+8 г) 8-1 д) -5-6 е) -5+4 ё) -9+13 | ж) -16+29 з) -27+43 и) -81+28 й) -324-41 к) 438-439 л) -428-49 м) -112-52 | н) 54-223 о) -37+54 п) -73-98 р) 11-27 с) -3+55 т) -8·(-2) у) 5·(-12) | ф) -15·8 х) -13·(-8) ц) -3·49 ч) 26·(-17) ш) -17·(-71) щ) 13·(-11) ъ) -12:(-4) | ы) -63:(-7) ь) -81:9 э) 54:(-9) ю) -32:(-8) я) -90:30 аа) 56:(-7) бб) -42:7 |
2.Выполнить действия с обыкновенными дробями:
| | | | |
3.Выполнить действия с десятичными дробями:
| а) 0,853+3,75 б) 4,27+15,373 в) 2,11+11,303 г) 21,5+17,205 д) -31,4+18,71 е) -2,37+41,237 ё) 16,22+22,16 ж) 3,19+17,251 | з) 3,54-2,873 и) 5,251-3,1 й) -4,52-2,573 к) -9,11-33,425 л) 2,11-9,121 м) 7,3-14,253 н) 39,3-11,43 о) 65,21-3,18 | п) 5·0,58 р) 2,6·15 с) 14·2,05 т) 15·0,25 у) 5,7·1,13 ф) 1,08·3,8 х) 3,75·0,032 ц) 1,25·0,016 | ч) 14,6:4 ш) 0,144:12 щ) 0,861:7 ъ) 17:8 ы) 5:8 ь) 0,1853:0,17 э) 11:0,04 ю) 0,7344:0,24 |
4.Перевести проценты в дробь (обыкновенную или десятичную):
| а) 3% б) 5% в) 7% г) 15% | д) 11% е) 35% ё) 27% ж) 55% | з) 107% и) 120% к) 123% л) 150% | м) 217% н) 50% о) 70% п) 269% |
5.Перевести дробь в проценты:
| | | | |
6.Найти процент от числа:
| а) 15% от 1000 рублей б) 19% от 1200 рублей в) 50% от 3 км г) 10% от 1 км | д) 120% от 3000 рублей е) 180% от 50 грамм ё) 150% от 200 км ж) 125% от 700 км |
7.Найти число, если:
| а) 15% от числа равны 450 б) 30% от числа равны 6900 в) 50% от числа равны 2400 г) 35% от числа равны 1050 | д) 25% от числа равны 400 е) 75% от числа равны 1200 ё) 120% от числа равны 1860 ж) 200% от числа равны 394 |
8.Решить задачи на проценты:
а) Напиток содержит 50% сои, 14% ячменя, 30% свеклы, 6% шиповника. Определите массу каждой составляющей в 500 грамм такого напитка.
б) После очистки зерен пшеницы от семян сорной травы ее масса уменьшается на 15%. На сколько уменьшится масса при очистке 1600 грамм засоренной пшеницы? Сколько чистой пшеницы при этом получится?
в) В библиотеке 200 учебников, что составляет 4% всех книг. Сколько книг в библиотеке?
г) В соревнованиях участвовали 600 школьников. Среди них 65% - мальчики. Сколько девочек участвовало в соревнованиях?
д) В коробке 100 геометрических фигур для уроков математики. Среди этих фигур 20% - квадраты, из них 25% - квадраты красного цвета. Сколько в коробке красных квадратов?
е) Цена книги понизилась на 15%. Найдите новую цену книги, если прежняя составляла 80 рублей.
ж) Флакон духов стоит 3000 рублей. Во время проведения акции цена на духи уменьшилась на 15%. Можно ли купить два флакона этих духов на 5000 рублей?
з) Супермен, совершив в понедельник 25 подвигов, решил, что каждый день в течение недели он будет совершать на 20% подвигов больше, чем в предыдущий день. Сколько подвигов должен совершить супермен в среду согласно своему плану?
и) На контрольной работе по математике 20% шестиклассников получили оценку 5. Сколько учеников в классе, если оценку 5 получили 5 человек?
к) Фигурным катанием занимаются 12% шестиклассников школы. Сколько человек занимаются фигурным катанием, если в школе 150 шестиклассников?
9.Найти значение выражений:
| а) (-15,64: б) (0,4 в) 0,8: г) д) е) | 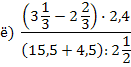 |
10.Раскройте скобки и упростите выражения (приведите подобные):
| а) 2х-(2х+у)+у б) –а+(2а – b)+2b в) 7-(с+14) – 2с | г) 3у – (18+у) +8 д) –(7-х)+(3х – 14) е) –(х+4) – (2х – 8) | ё) (21-а) – (20-2а) ж) –(13+с) +(-с – 13) з) 2(3-х) – (8+х) | и) -4(у+5)+(12 – у) й) –(7-х)+4(х – 5) к) -9(у – 4) – (12+у) |
11.Решить уравнения:
| | |
12.Решите задачи на движение:
а) Из лагеря вышла группа туристов и отправилась к озеру со скоростью 4 км/ч. Через 1,5 часа вслед за ними выехал велосипедист со скоростью 12 км/ч. Через какое время велосипедист догонит туриста?
б) Из села в город выехал велосипедист со скоростью 11,5 км/ч. Через 2,4 часа вслед за ним выехал мотоциклист со скоростью 46 км/ч. Через сколько часов и на каком расстоянии от города мотоциклист догонит велосипедиста, если от села до города 40 км?
в) Из двух городов, расстояние между которыми 420 км, одновременно навстречу друг другу выехали грузовая машина со скоростью 60 км/ч и легковая – со скоростью 80 км/ч. Через сколько часов после их встречи грузовая машина прибудет в пункт назначения?
г) Расстояние от дома до школы 825 метров. Миша прошел это расстоянии за 12 минут. Определите скорость ( в м/с), с которой он шел.
д) Пешеход поделал путь от одного поселка до другого за 4,5 часа со скоростью 4 км/ч. С какой скоростью должен идти пешеход, чтобы проделать этот путь за 3 часа?
е) Из двух городов, расстояние между которыми равно 240 км, одновременно навстречу друг другу выехали два автомобиля. Скорость одного из них 62,3, что на 2,4 км/ч меньше скорости другого. Найдите расстояние между автомобилями через 1 час после начала движения.
ё) Собственная скорость теплохода 27км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними 120 км?
ж) Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению реки и 3 часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
з) Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч?
и) Скорость моторной лодки в стоячей воде 15км/ч, а скорость течения реки 3 км/ч.
Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км?
13.Решите задачи с помощью уравнения или алгебраически (по действиям):
а) В одном мешке в 5 раз больше крупы, чем в другом. После того, как из первого мешка пересыпали во второй 27 кг, крупы в обоих мешках стало поровну. Сколько всего килограмм крупы было в каждом мешке сначала?
б) На первой полке в 8 раз больше книг, чем на второй. Если с первой полки снять 4 книги, а на вторую поставить 10 книг, то книг на полках станет поровну. На сколько больше книг было на первой полке, чем на второй?
в) Ширина прямоугольного садового участка на 7,8 м меньше его длины, а периметр равен 100 м. Найдите площадь участка.
г) За 9 часов культиватор обрабатывает площадь 0,7 га.За какое время он обработает 3,5 га?
д) Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 штук. Девочка сорвала в 2 раза меньше мальчика. Сколько орехов было у мальчика и у девочки отдельно?