Файл: Практическая работа 1 Фамилия Сафронов Имя Сергей Отчество Максимович.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 11
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Кафедра информационных управляющих систем
Дисциплина: Основы теории управления
ПРАКТИЧЕСКАЯ РАБОТА № 1
Фамилия: Сафронов Имя: Сергей
Отчество: Максимович
Номер зачётной книжки: 1910464
Специальность: Информационные системы и технологии
Курс: 2
Факультет: ИНО
Группа №: ИБ-06с
Проверил(а):
Санкт-Петербург
2022
Дано апериодическое звено второго порядка, передаточная функция которого:
w (s) = —
( ) T1T2S2 + T2fs + 1
где k1 - коэффициент усиления;
T1 и T2- постоянные времени, с;
0 < £ < 1 - коэффициент демпфирования.
Необходимо построить переходные характеристики при значениях
-
£ = 0;
-
£ = 0,2;
-
£ = 0,5;
-
^ =1.
По полученным переходным характеристикам рассчитать перерегулирование, время регулирования, амплитуду колебаний, частоту колебаний (не все параметры присущи каждой полученной переходной характеристике).
Значение k1 выбирается по последней цифре номера студенческого билета, если последняя цифра равна 0, то k1=10.
к1 к1
к1 = Последний номер студенческого билета; к1 = k2;T1 = —; T2 = —.
Номер студенческого билета: 1910464.
Вариант: 4.
^1 = 4; ^1 = ^2; T1 = ТГТ; T2 = ТТ7
1 1 2 1 30 2 10
Модель в MatLab
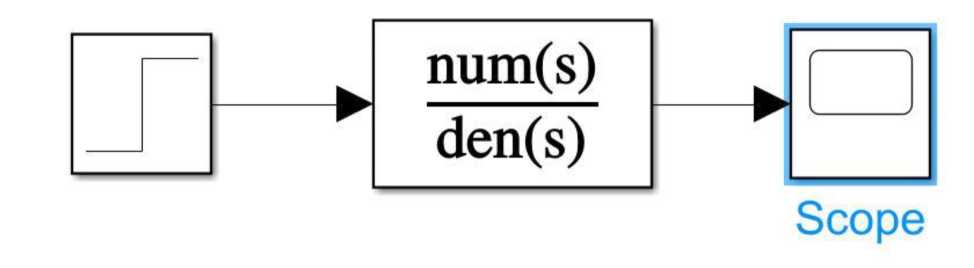
Рис. 1. Модель в MatLab
Ж(^) =
4 4
30 10
4
s2 + уд 0s + 1
16 2X1
300s +1
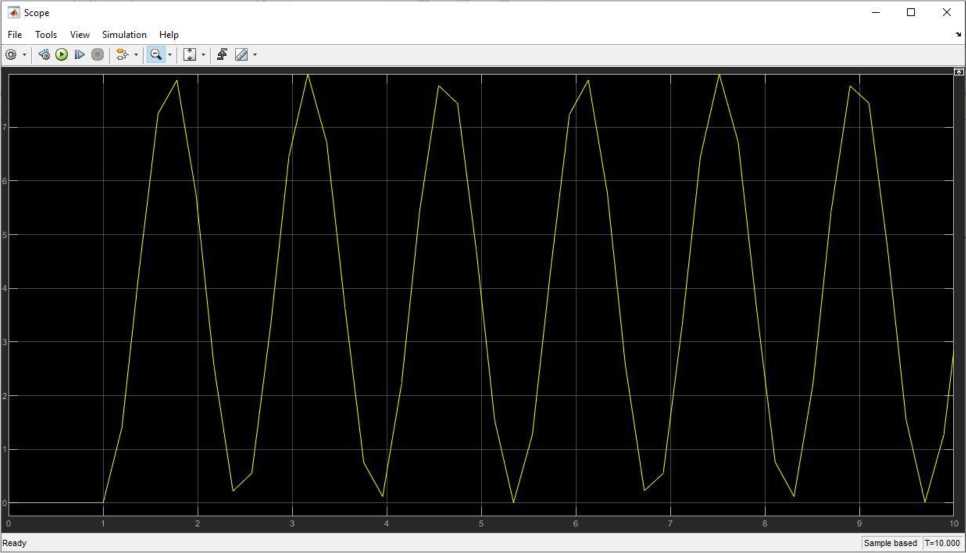
Переходная характеристика при £ = 0:
Рис. 2. Переходная характеристика
Амплитуда А « 8
Частота колебаний м « 1,25.
4
Ms) = 4Г4 4



4
^6s2 + 0.8 s + 1
О kJ kJ
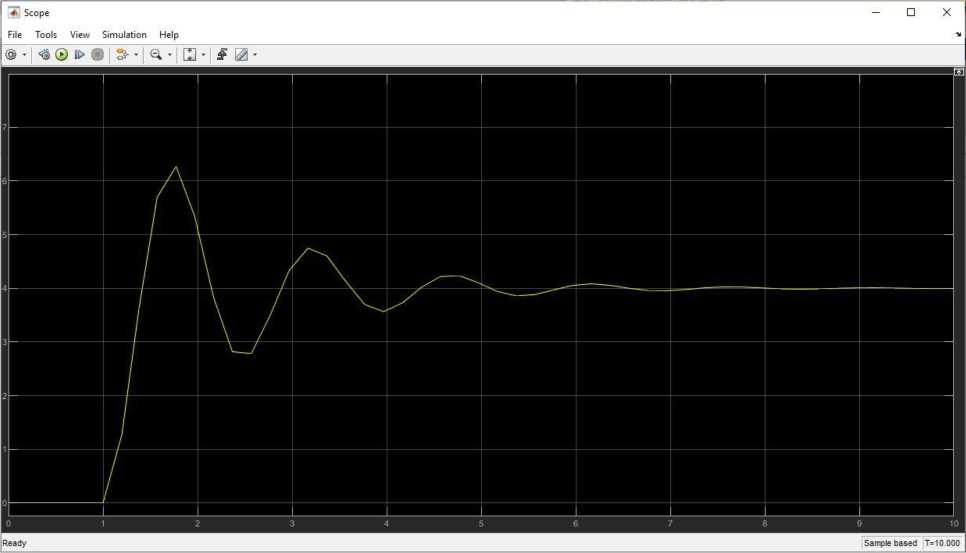
Переходная характеристика при £ = 0.2:
Рис. 3. Переходная характеристика
30 10s2 + 10 0.2s + 1
Установившееся значение ууст = 4
Максимальное значение утй% — 6,2 Перерегулирование составило: 8 = 55% Время регулирования составило р — 4,5с
Ж(^) =
44
30 10s
4
+ уд 0.5 s + 1
4
“4 " Z
ST2S 2 + 2 s + 1
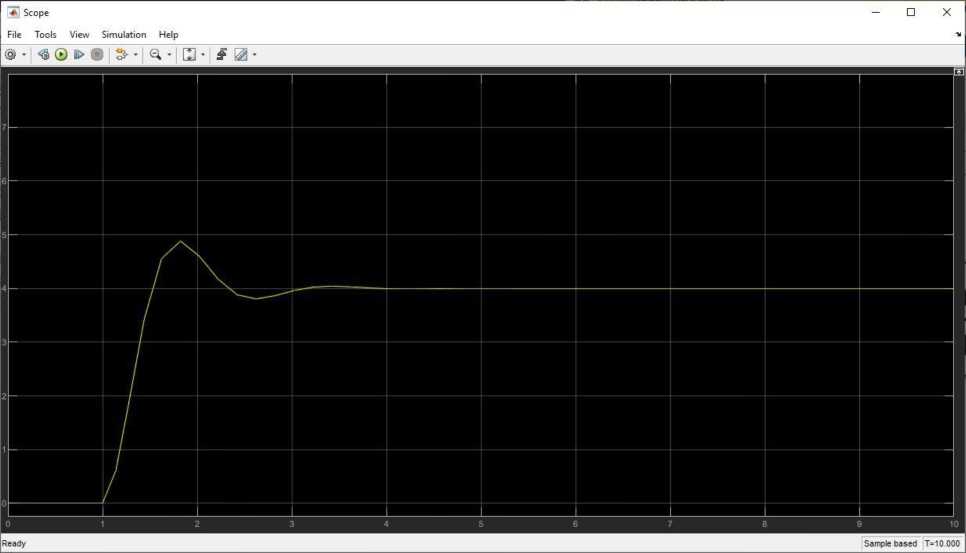
Переходная характеристика при £ = 0.5:
Рис. 4. Переходная характеристика
Установившееся значение ууст = 4
Максимальное значение утах 4,9 Перерегулирование составило: S = 22,5% Время регулирования составило £р « 2,5 с

Ж(^) =
4
— — s2+— 1s + 1

4
4
s + 0.4 s + 1
О V/
30 10 5 + 10 1 5 + 1
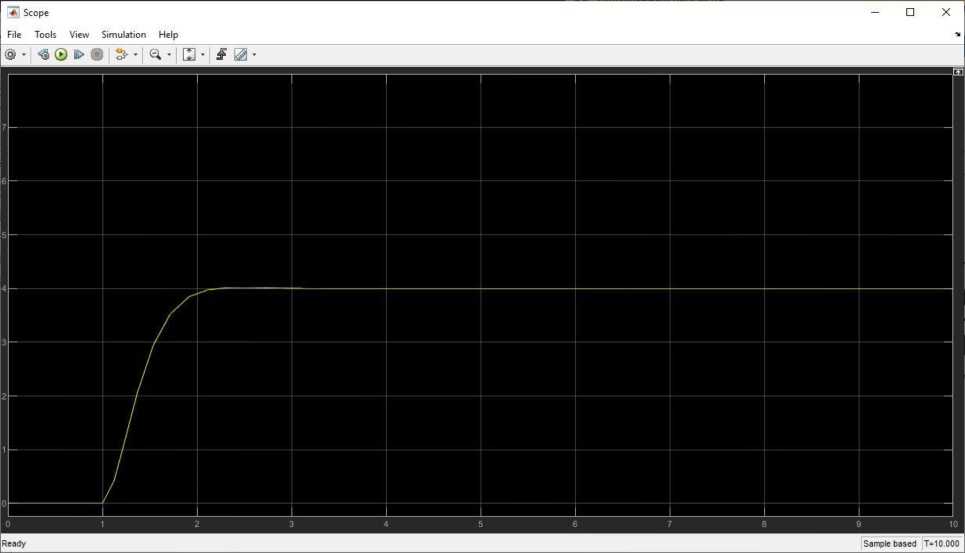
Переходная характеристика при £ = 1:
Рис. 5. Переходная характеристика
Установившееся значение ууст = 4
Максимальное значение утах
4,001 Перерегулирование составило: S = 0,025% Время регулирования составило tp
2,1 с
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Кафедра информационных управляющих систем
Дисциплина: Основы теории управления
ПРАКТИЧЕСКАЯ РАБОТА № 1
Фамилия: Сафронов Имя: Сергей
Отчество: Максимович
Номер зачётной книжки: 1910464
Специальность: Информационные системы и технологии
Курс: 2
Факультет: ИНО
Группа №: ИБ-06с
Проверил(а):
Санкт-Петербург
2022
Дано апериодическое звено второго порядка, передаточная функция которого:
w (s) = —
( ) T1T2S2 + T2fs + 1
где k1 - коэффициент усиления;
T1 и T2- постоянные времени, с;
0 < £ < 1 - коэффициент демпфирования.
Необходимо построить переходные характеристики при значениях
-
£ = 0;
-
£ = 0,2;
-
£ = 0,5;
-
^ =1.
По полученным переходным характеристикам рассчитать перерегулирование, время регулирования, амплитуду колебаний, частоту колебаний (не все параметры присущи каждой полученной переходной характеристике).
Значение k1 выбирается по последней цифре номера студенческого билета, если последняя цифра равна 0, то k1=10.
к1 к1
к1 = Последний номер студенческого билета; к1 = k2;T1 = —; T2 = —.
Номер студенческого билета: 1910464.
Вариант: 4.
^1 = 4; ^1 = ^2; T1 = ТГТ; T2 = ТТ7
1 1 2 1 30 2 10
Модель в MatLab

Рис. 1. Модель в MatLab
Ж(^) =
4 4
30 10
4
s2 + уд 0s + 1
16 2X1
300s +1

Переходная характеристика при £ = 0:
Рис. 2. Переходная характеристика
Амплитуда А « 8
Частота колебаний м « 1,25.
4
Ms) = 4Г4 4




4
^6s2 + 0.8 s + 1
О kJ kJ
Переходная характеристика при £ = 0.2:
Рис. 3. Переходная характеристика
30 10s2 + 10 0.2s + 1
Установившееся значение ууст = 4
Максимальное значение утй% — 6,2 Перерегулирование составило: 8 = 55% Время регулирования составило р — 4,5с

Ж(^) =
44
30 10s
4
+ уд 0.5 s + 1
4
“4 " Z
ST2S 2 + 2 s + 1
Переходная характеристика при £ = 0.5:
Рис. 4. Переходная характеристика
Установившееся значение ууст = 4
Максимальное значение утах 4,9 Перерегулирование составило: S = 22,5% Время регулирования составило £р « 2,5 с

Ж(^) =
4
— — s2+— 1s + 1

4
4
s + 0.4 s + 1
О V/
30 10 5 + 10 1 5 + 1

Переходная характеристика при £ = 1:
Рис. 5. Переходная характеристика
Установившееся значение ууст = 4
Максимальное значение утах
4,001 Перерегулирование составило: S = 0,025% Время регулирования составило tp
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Кафедра информационных управляющих систем
Дисциплина: Основы теории управления
ПРАКТИЧЕСКАЯ РАБОТА № 1
Фамилия: Сафронов Имя: Сергей
Отчество: Максимович
Номер зачётной книжки: 1910464
Специальность: Информационные системы и технологии
Курс: 2
Факультет: ИНО
Группа №: ИБ-06с
Проверил(а):
Санкт-Петербург
2022
Дано апериодическое звено второго порядка, передаточная функция которого:
w (s) = —
( ) T1T2S2 + T2fs + 1
где k1 - коэффициент усиления;
T1 и T2- постоянные времени, с;
0 < £ < 1 - коэффициент демпфирования.
Необходимо построить переходные характеристики при значениях
-
£ = 0;
-
£ = 0,2;
-
£ = 0,5;
-
^ =1.
По полученным переходным характеристикам рассчитать перерегулирование, время регулирования, амплитуду колебаний, частоту колебаний (не все параметры присущи каждой полученной переходной характеристике).
Значение k1 выбирается по последней цифре номера студенческого билета, если последняя цифра равна 0, то k1=10.
к1 к1
к1 = Последний номер студенческого билета; к1 = k2;T1 = —; T2 = —.
Номер студенческого билета: 1910464.
Вариант: 4.
^1 = 4; ^1 = ^2; T1 = ТГТ; T2 = ТТ7
1 1 2 1 30 2 10
Модель в MatLab

Рис. 1. Модель в MatLab
Ж(^) =
4 4
30 10
4
s2 + уд 0s + 1
16 2X1
300s +1

Переходная характеристика при £ = 0:
Рис. 2. Переходная характеристика
Амплитуда А « 8
Частота колебаний м « 1,25.
4
Ms) = 4Г4 4




4
^6s2 + 0.8 s + 1
О kJ kJ
Переходная характеристика при £ = 0.2:
Рис. 3. Переходная характеристика
30 10s2 + 10 0.2s + 1
Установившееся значение ууст = 4
Максимальное значение утй% — 6,2 Перерегулирование составило: 8 = 55% Время регулирования составило р — 4,5с

Ж(^) =
44
30 10s
4
+ уд 0.5 s + 1
4
“4 " Z
£ = 0;
£ = 0,2;
£ = 0,5;
^ =1.
Ж(^) =
4 4
30 10
4
s2 + уд 0s + 1
16 2X1
300s +1

Переходная характеристика при £ = 0:
Рис. 2. Переходная характеристика
Амплитуда А « 8
Частота колебаний м « 1,25.
4
Ms) = 4Г4 4




4
^6s2 + 0.8 s + 1
О kJ kJ
Переходная характеристика при £ = 0.2:
Рис. 3. Переходная характеристика
30 10s2 + 10 0.2s + 1
Установившееся значение ууст = 4
Максимальное значение утй% — 6,2 Перерегулирование составило: 8 = 55% Время регулирования составило р — 4,5с
ST2S 2 + 2 s + 1
Переходная характеристика при £ = 0.5:
Рис. 4. Переходная характеристика
Установившееся значение ууст = 4
Максимальное значение утах 4,9 Перерегулирование составило: S = 22,5% Время регулирования составило £р « 2,5 с

Ж(^) =
4
— — s2+— 1s + 1

4
4

Переходная характеристика при £ = 1:
Рис. 5. Переходная характеристика