Файл: Лекция Колебания кристаллической решетки Лекция Модель свободных электронов металла.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 21.11.2023
Просмотров: 75
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
по курсу «Физика твердого тела»
для студентов 2 курса
Модель свободных электронов металла
-
Ознакомьтесь с теоретическим материалом в курсе лекций
Лекция 4. Колебания кристаллической решетки
Лекция 5. Модель свободных электронов металла
Лекция 6. Зонная теория кристаллов. Полупроводники и диэлектрики
Лекция 7. Контактные явления ................................................ .................. https://edu.stankin.ru/mod/resource/view.php?id=338195
и в лекциях
Колоколов А.А. Избранные главы физики: конспект лекций / А.А.Колоколов. – М.: ФГБОУ ВПО МГТУ «СТАНКИН», 2015. – 89с.:ил.
https://edu.stankin.ru/mod/resource/view.php?id=336602
-
Ознакомьтесь с разбором и ходом решения задач
Задача №1
Условие
Концентрация электронов проводимости в германии при комнатной температуре n = 3·10 19 м-3. Плотность германия 5400 кг/м3, молярная масса германия 0,073 кг/моль. Каково отношение числа электронов проводимости к общему числу атомов?

Задача №2
Условие
По тонкой кремниевой пластинке шириной l = 3,2 мм и толщиной d = 250 мкм течет ток I = 5,2 мА. Кремний содержит примеси фосфора и является полупроводником n-типа. Число электронов в единице объема во много раз превышает концентрацию носителей заряда в чистом кремнии. Для данного образца концентрация электронов составляет nе = 1,5·10 23 м-3. Определите среднюю дрейфовую скорость электронов.

Задача №3
В цепь, состоящую из последовательно соединенных резистора с сопротивлением r = 1 кОм и термистора – полупроводникового прибора, электрическое сопротивление которого сильно зависит от температуры, включен источник постоянного тока. Температурная характеристика термистора приведена на рисунке.
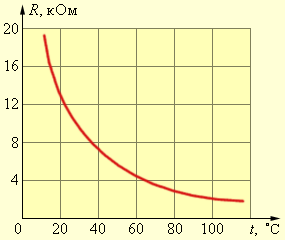
Во сколько раз изменится сила тока I в цепи, если термистор, находившийся первоначально при комнатной температуре t1 = 20 °C, нагреть до 100 °C?
Решение
Сопротивление термистора при комнатной температуре t1 = 20 °C равно R1 = 13 кОм. При температуре t2 = 100 °C сопротивление термистора равно R2 = 2 кОм. Из закона Ома следует, что ток в цепи обратно пропорционален полному сопротивлению цепи. Таким образом,
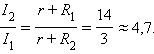
Задача №4
Условие
В усилителе, собранном на транзисторе по схеме с общей базой, сила тока в цепи эмиттера равна 12 мА, в цепи базы 600 мкА. Найти силу тока в цепи коллектора.
Решение
Сила тока в цепи коллектора будет равна разности сил тока в цепях эмиттера и базы:
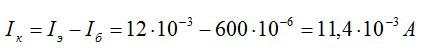
Ответ: 11,4 мА
Задача №5
Условие
Расстояние между катодом и анодом вакуумного диода равно 1 см. Сколько времени движется электрон от катода к аноду при анодном напряжении 440 В? Движение считать равноускоренным.
Решение
Начальную скорость электрона будем считать равной нулю. По закону сохранения энергии:
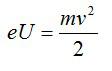
Отсюда выразим скорость:
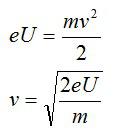
По 2 закону Ньютона, со стороны электрического поля на электрон действует сила, которая сообщает ему посоянное ускорение:
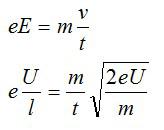
Выразим время и вычислим:
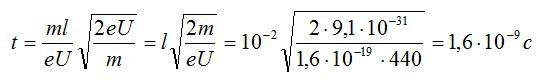
Ответ: 1,6 нс.
Задача №6
По тонкой кремниевой пластинке шириной l = 3,2 мм и толщиной d = 250 мкм течет ток I = 5,2 мА. Кремний содержит примеси фосфора и является полупроводником n-типа. Число электронов в единице объема во много раз превышает концентрацию носителей заряда в чистом кремнии. Для данного образца концентрация электронов составляет nе = 1,5·1023 м–3. Определите среднюю дрейфовую скорость 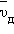 электронов.
электронов.
Решение
В примесных полупроводниках n-типа концентрация электронов во много раз превышает концентрацию дырок. Поэтому ток в полупроводниках n-типа практически полностью обусловлен дрейфом электронов под действием приложенного электрического поля.
Плотность тока j, т. е. сила тока, протекающего через единичное сечение образца, равна
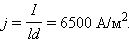
Дрейфовая скорость электронов находится из выражения
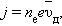
где e – заряд электрона. Отсюда
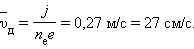
Полученное значение дрейфовой скорости электронов в кремниевом полупроводнике n-типа на несколько порядков превышает дрейфовую скорость электронов в металлических проводниках.
Задача 7
Считая, что энергия Ферми для Na равна Ef=3,1 эВ и наблюдаемая электропроводность
=2,1107 Ом-1 м –1 при температуре Т = О К, рассчитать время релаксации (характерное время) .
Решение.
Время релаксации определим, преобразуя формулу Друде:
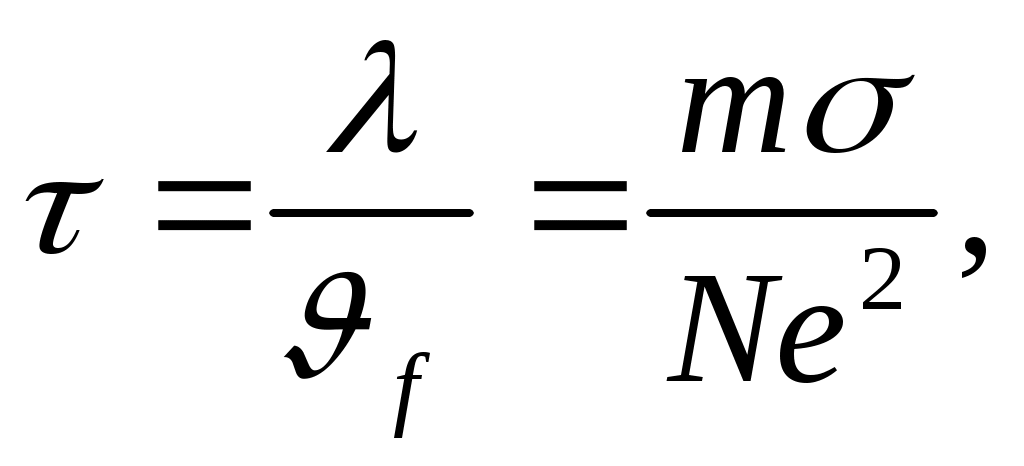
где - средняя длина свободного пробега электронов, f- скорость Ферми, N – плотность электронов проводимости. 
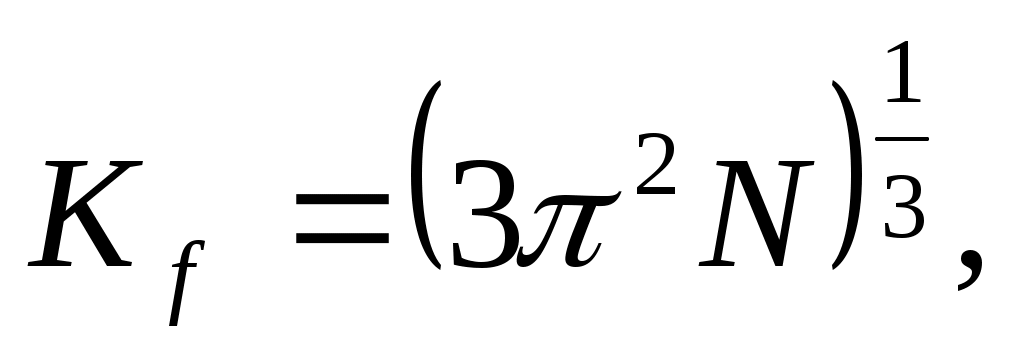
Величину N получим, зная энергию Ферми. Поскольку для свободных электронов поверхность Ферми представляет собой сферу радиусом
а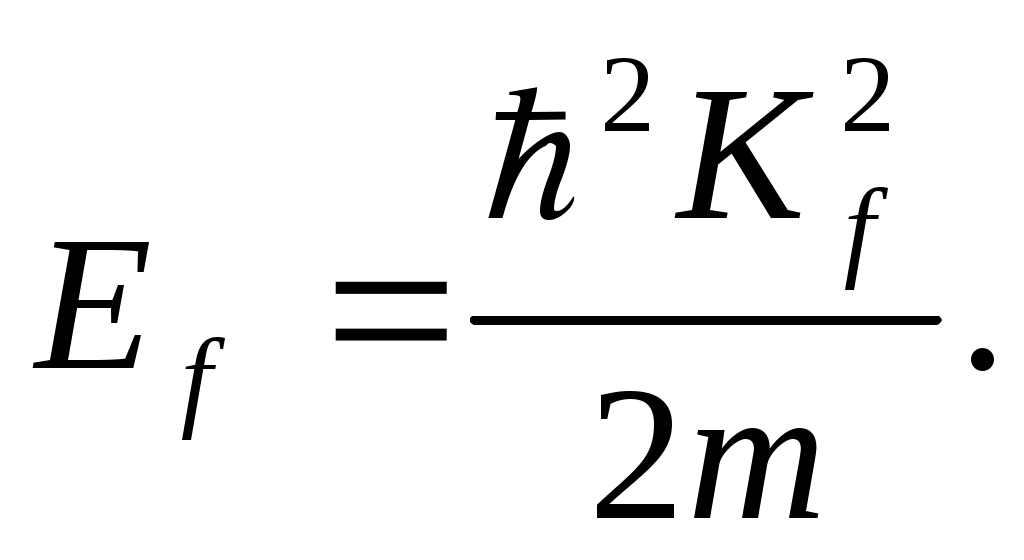
энергия Ферми равна
Следовательно,
и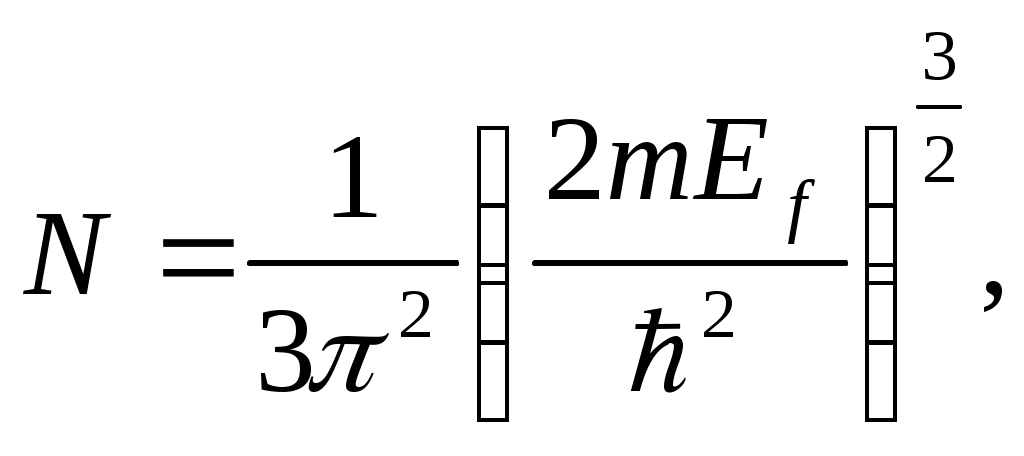
время релаксации равно
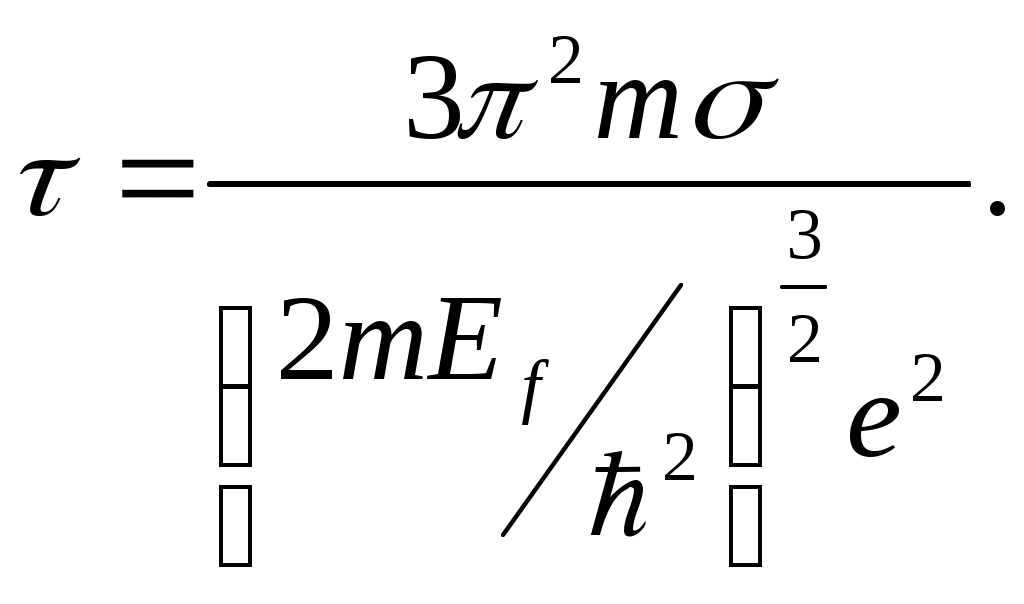
Подставляя значения получаем: = 310-14c.
Задача 8
Определить внутреннюю и внешнюю контактную разность потенциалов при комнатной температуре (
300 К) для двух металлов, имеющих энергию Ферми Ef1 = 3 эВ и Ef2 = 2 эВ и работу выхода, соответственно А1 = 1 эВ и А= 1,5 эВ.
Анализ и решение
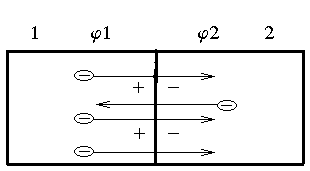
При контакте двух металлов вследствие теплового движения электроны, энергия которых достаточна для того, чтобы покинуть металл, начнут проходить через границу раздела металлов. Чем меньше работа выхода металла (т.е. наименьшая энергия, которую надо сообщить электрону проводимости металла, чтобы он покинул металл и перешел в вакуум), тем больше таких электронов. В нашей задаче работа выхода металла 1 меньше, чем работа выхода металла 2. В
этом случае из первого металла будет уходить в металл 2 больше число электронов, чем из металла 2 в металл 1.
Это неодинаковое движение электронов в противоположных направлениях приведёт к тому, что в металле 2 вблизи контакта образуется избыточный отрицательный заряд, а в металле 1, из которого ушло электронов больше, чем пришло в него, возникает избыточный положительный заряд.
Таким образом, при контакте двух металлов возникает двойной электрический слой (контактный слой). При этом металл 1 заряжен положительно, а металл 2 отрицательно. Одновременно происходит относительное смещение энергетических уровней электронов в контактирующих металлах. В металле 1 все уровни смещаются вниз, а в металле 2 – вверх. Это происходит для установления равновесия, когда сравниваются электрохимические потенциалы (e) двух контактирующих металлов. Поэтому из условия равновесия для контакта двух металлов имеем:
ee , (1)
где 1 и2 – равновесные значения потенциалов 1-го и 2-го металлов;
1 и2 – химические потенциалы электронного газа в 1-ом и во 2-ом металле.
В квантовой статистике электроны проводимости рассматриваются в приближении вырожденного электронного газа, подчиняющегося статистике Ферми-Дирака. Согласно этому приближению химический потенциал электронного газа связан с энергией Ферми Ef следующей формулой:
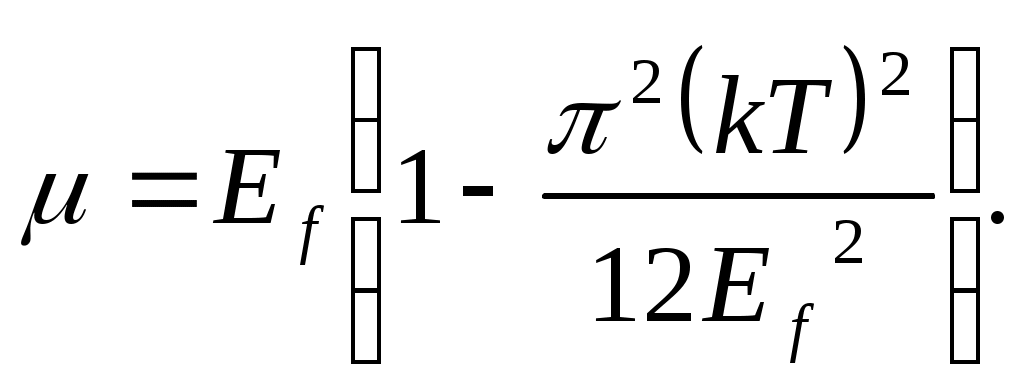
Таким образом, при Т=0 К равен верхнему занятому электронами энергетическому уровню – уровню Ферми с энергией Ef , а повышение температуры приводит к медленному убыванию .
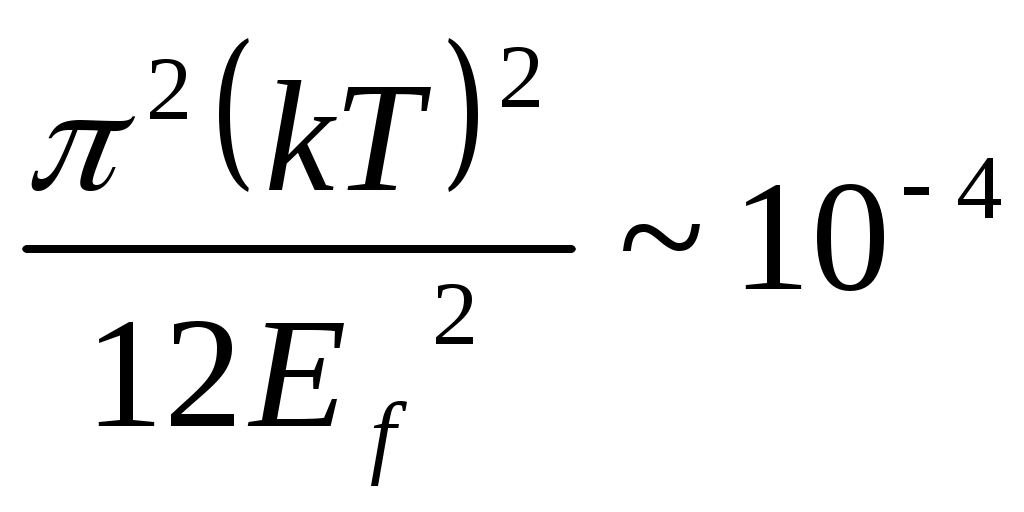
При комнатной температуре (Т=300 К) величина
и можно с достаточно большой точностью считать = Ef.
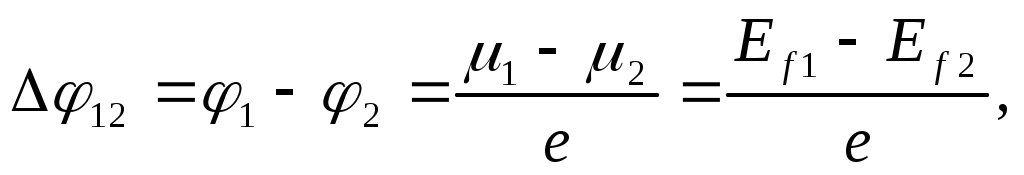
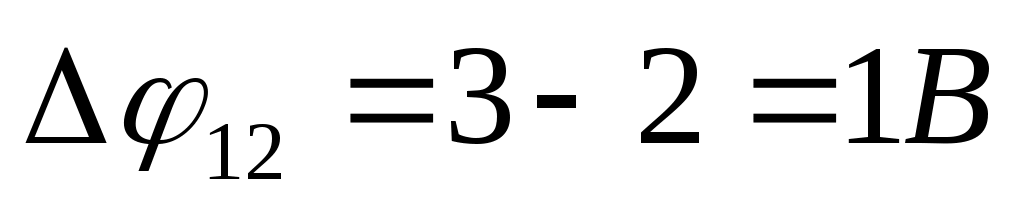
Тогда из формулы (1) получаем выражение для внутренней контактной разности потенциалов 12:
Внешняя контактная разность потенциалов определяется как разность потенциалов между двумя точками, находящимися вблизи поверхности первого (' ) и второго (' ) контактирующих металлов.
Из известной формулы работы выхода А = е(-') -
и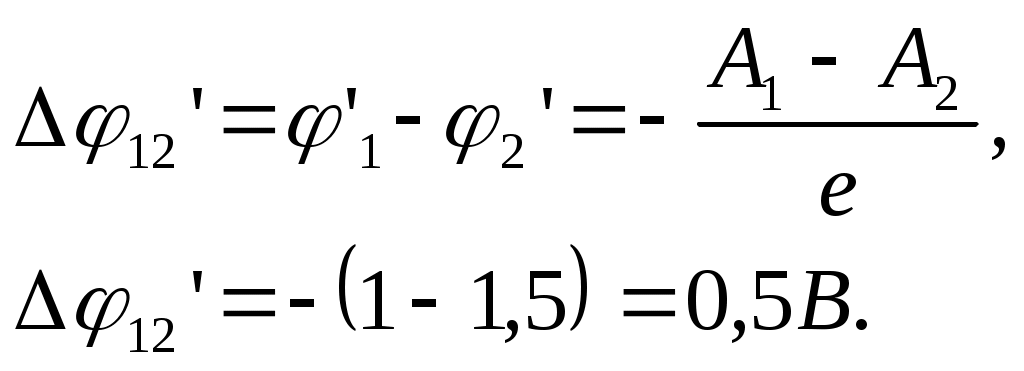
из условия равенства электрохимических потенциалов электронов в контактирующих металлах (1) получаем, что внешняя контактная разность потенциалов 12’ равна:
Задача № 9*
Определите температуру, при которой в твердом проводнике вероятность найти электрон с энергией 0,5 эВ над уровнем Ферми равна 1%.
Решение
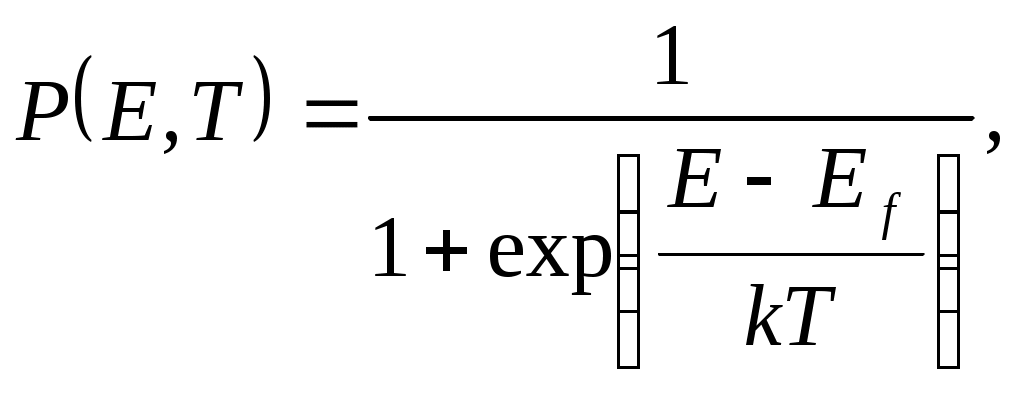
Электроны как частицы с полуцелым спином подчиняются статистике Ферми-Дирака. Функция распределения Ферми-Дирака записывается следующим образом:
где P(E,T) – вероятность того, что электрон занимает энергетический уровень Е, расположенный выше или ниже уровня Ферми Еf.
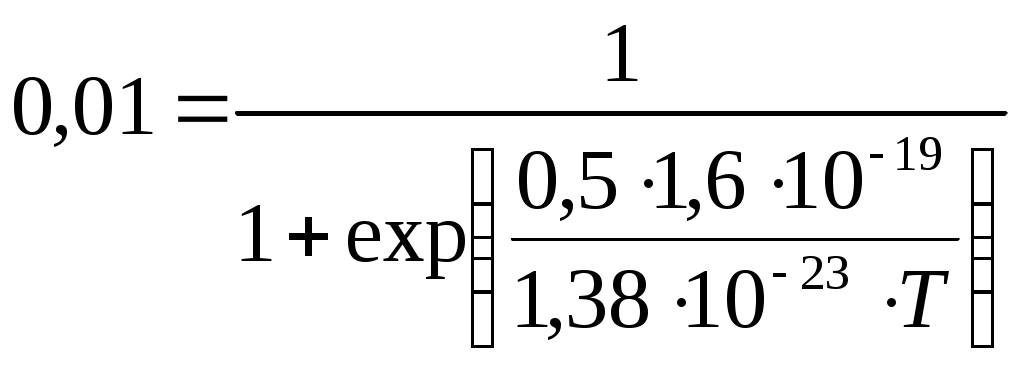
Подставим в последнее выражение значение вероятности 1%, т.е. полагая Р(Е,Т)=0,01, получим
или
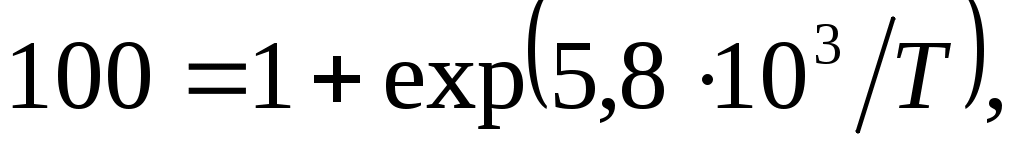
т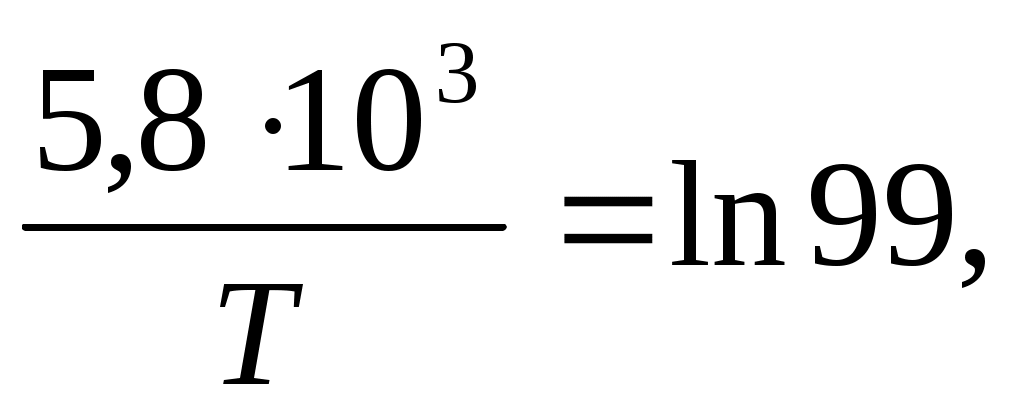
.е.
отсюда находим искомое значение температуры Т = 1262 К.
Электропроводность полупроводников
Задача 10
Определите положение уровня Ферми в германии n – типа при температуре 300 K, если на 106 атомов германия приходится 1 атом примеси. Принять концентрацию атомов в германии равной 4,41028 атомов в 1м3, ширину запрещенной зоны 0,72 эВ, расстояние между дном зоны проводимости и донорным уровнем 0,01 эВ, константу в выражении, связывающим число электронов в единице объема в зоне проводимости с температурой и энергией уровней, равной G = 4,831021м-3 (K)-3/2.
Решение
Электропроводность чистого полупроводника такого, как германий, может быть увеличена незначительным добавлением соответствующего элемента V группы периодической системы Менделеева. Так, в германий чаще всего добавляют мышьяк или сурьму. Концентрация этих добавок обычно порядка одного атома примеси на 106 атомов германия, их называют примесными атомами в чистом полупроводнике, или легирующими элементами. Примесные атомы имеют пять валентных электронов, а в атомах чистого германия их всего четыре. При комнатных температурах почти все дополнительные электроны являются свободными. Эти примесные атомы называют донорами и легированный ими материал имеет проводимость n – типа, т.к. в нем образуется дополнительное количество подвижных отрицательных носителей заряда (электронов).
Каждый донорный атом создает энергетический уровень, расположенный чуть ниже дна зоны проводимости (в германии этот уровень располагается на расстоянии 0,01эВ от дна зоны проводимости).

Зона проводимости
Поэтому с такого уровня электроны легко переходят в зону проводимости. Примесные атомы ионизуются и существуют внутри кристалла в виде неподвижных положительных зарядов. Вероятность того, что электрон имеет энергию, соответствующую зоне проводимости, намного больше в полупроводнике n-типа, чем в чистом полупроводнике.

Валентная зона
Ec
Донорный уровень



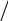
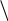

Запре-щенная зона Eg
Ev
E
Ef



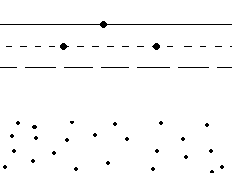
Следовательно, уровень Ферми находится между серединой запрещенной зоны и дном зоны проводимости.
По условию концентрация атомов в германии равна 4,41028м-3 и на 1106 атомов германия приходится 1 атом примеси, значит число свободных электронов в нем составит 4,41022 м -3.
Концентрация свободных электронов в германии определяется следующей формулой:
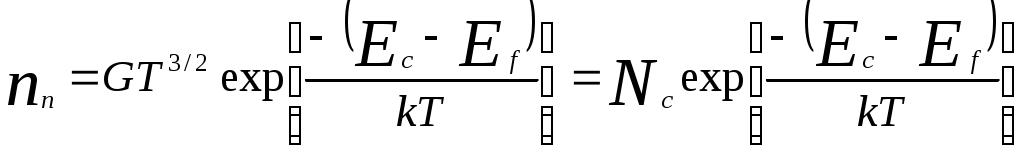 ,
,
где G = 4,831021м-3 (K)-3/2 – константа, связывающая число электронов в единице объема в зоне проводимости с температурой и энергией уровней,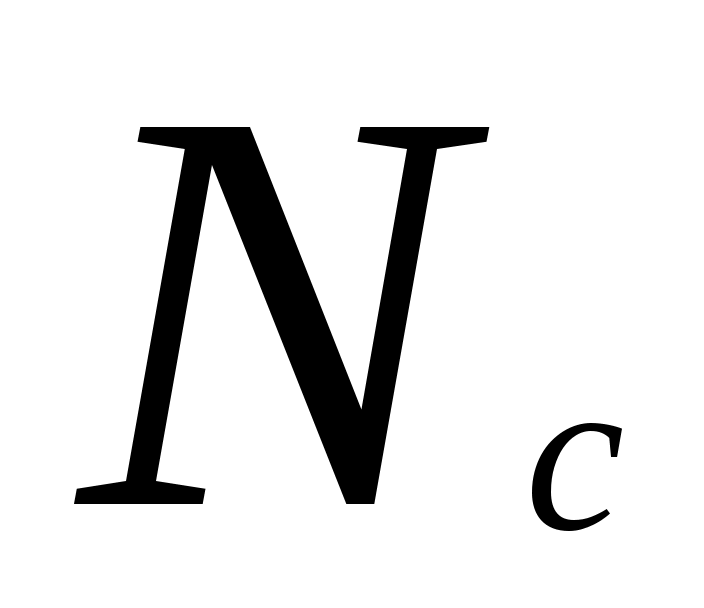 - эффективная плотность состояний в зоне проводимости, определяемая выражением:
- эффективная плотность состояний в зоне проводимости, определяемая выражением:
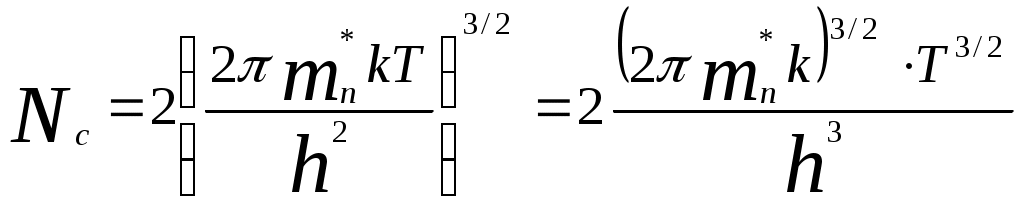 .
.
Поскольку разница между донорным уровнем и дном зоны проводимости равна 0,01эВ, а ширина запрещенной зоны Eg=0,72 эВ, то можно предположить, что все атомы примеси ионизованы, и пренебречь тепловой ионизацией примесных атомов.
Теперь можно вычислить величину 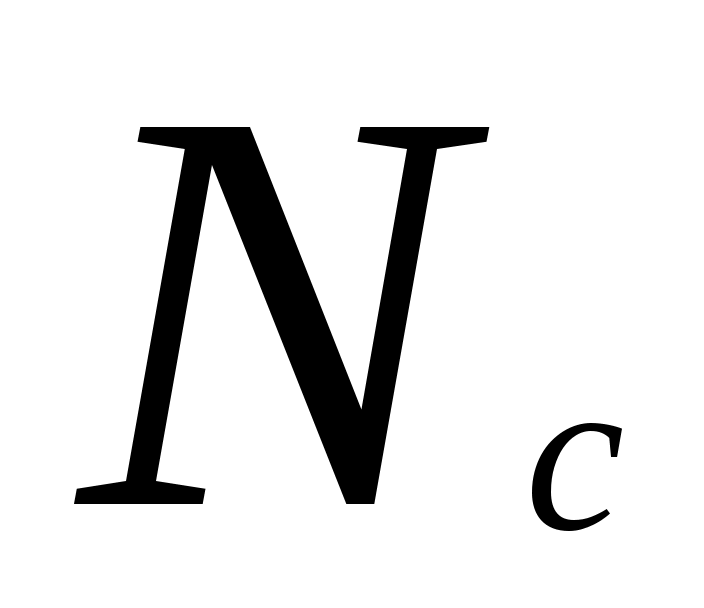 при заданной температуре T = 300K.
при заданной температуре T = 300K.
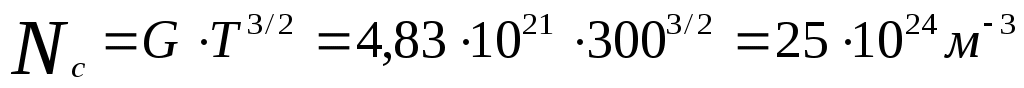 и поэтому
и поэтому
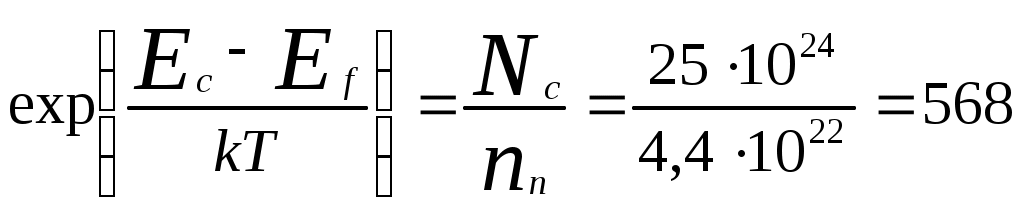 или
или 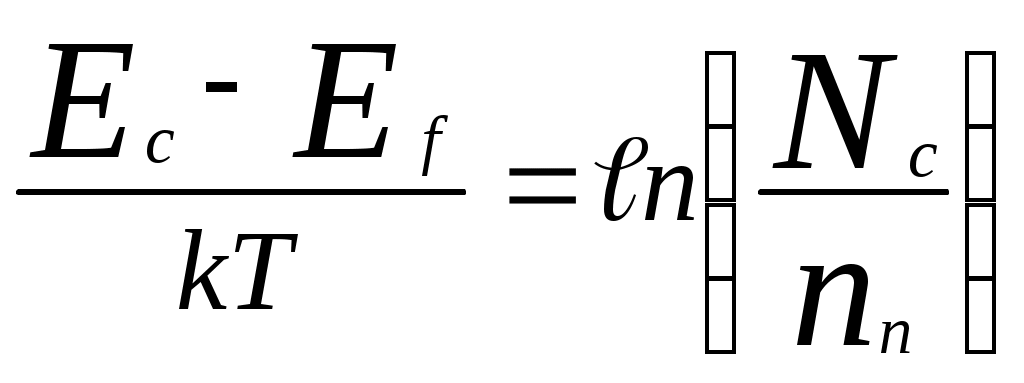 .
.
Отсюда получаем:
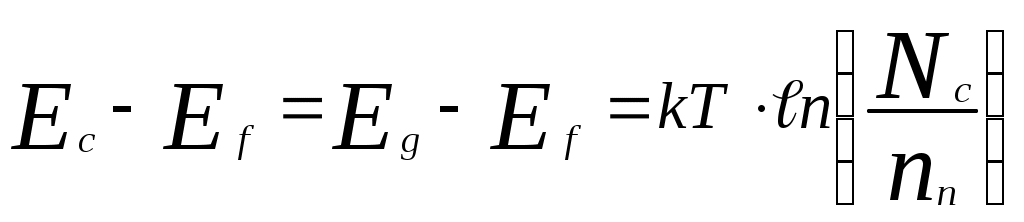 .
.
Таким образом : 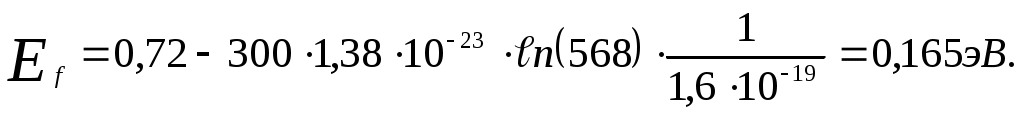
Это означает, что уровень Ферми находится на 0,165 эВ ниже дна зоны проводимости.
Задача 11
Определите коэффициент выпрямления К (отношение тока в прямом направлении к току в обратном направлении) p - n – перехода при температуре T =300 K и внешнем напряжении V = 0,2 В.
Решение
Если p – область соединить с анодом, а n – область – с катодом внешнего источника на
пряжения V (прямое направление), то потенциальный барьер уменьшается на 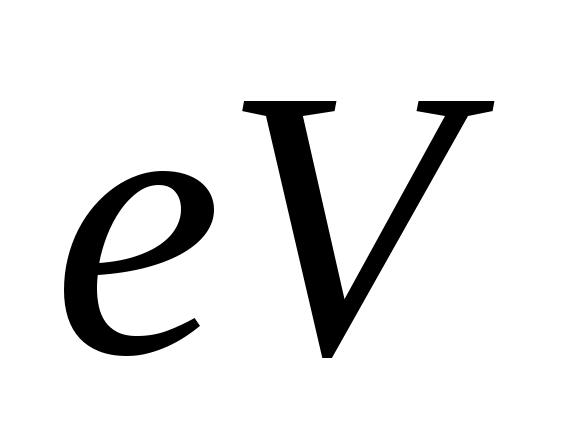 по сравнению с равновесным и происходит увеличение потока основных носителей, т.е. в p - область войдет добавочное количество электронов, а в n – область – дырок.
по сравнению с равновесным и происходит увеличение потока основных носителей, т.е. в p - область войдет добавочное количество электронов, а в n – область – дырок.
Полный ток через переход сложится из токов электронов и дырок и будет равен:
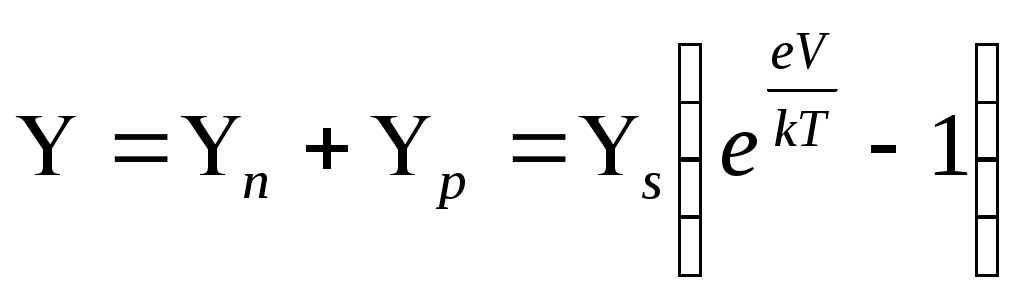 .
.
Если теперь p – область соединить с катодом, а n – область – с анодом внешнего источника напряжения V (обратное направление), то потенциальный барьер увеличится на 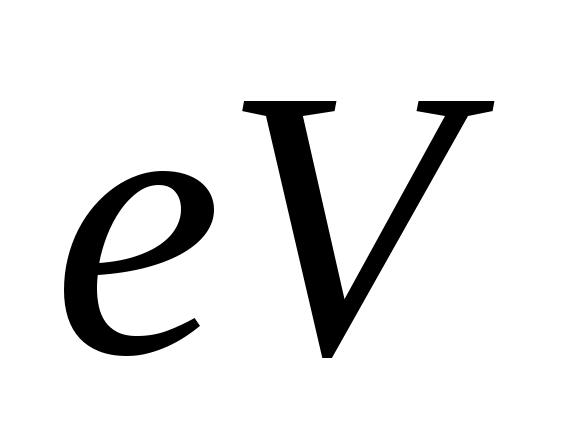 и это препятствует переходу электронов и дырок из областей, где они являются основными носителями. Обратный ток будет равен:
и это препятствует переходу электронов и дырок из областей, где они являются основными носителями. Обратный ток будет равен:
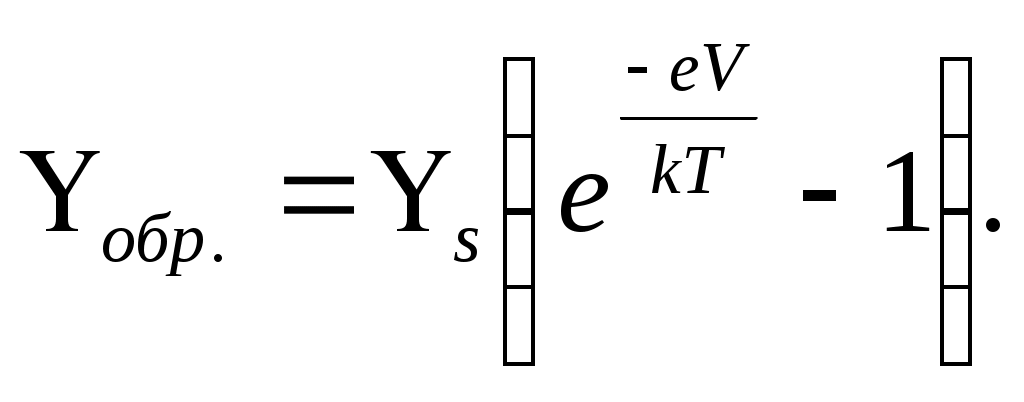
Вольт – амперная характеристика p – n – перехода имеет вид:

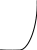



V
Y

Ys
Теперь определим отношение тока в прямом направлении к току в обратном направлении, часто называемое коэффициентом выпрямления K:
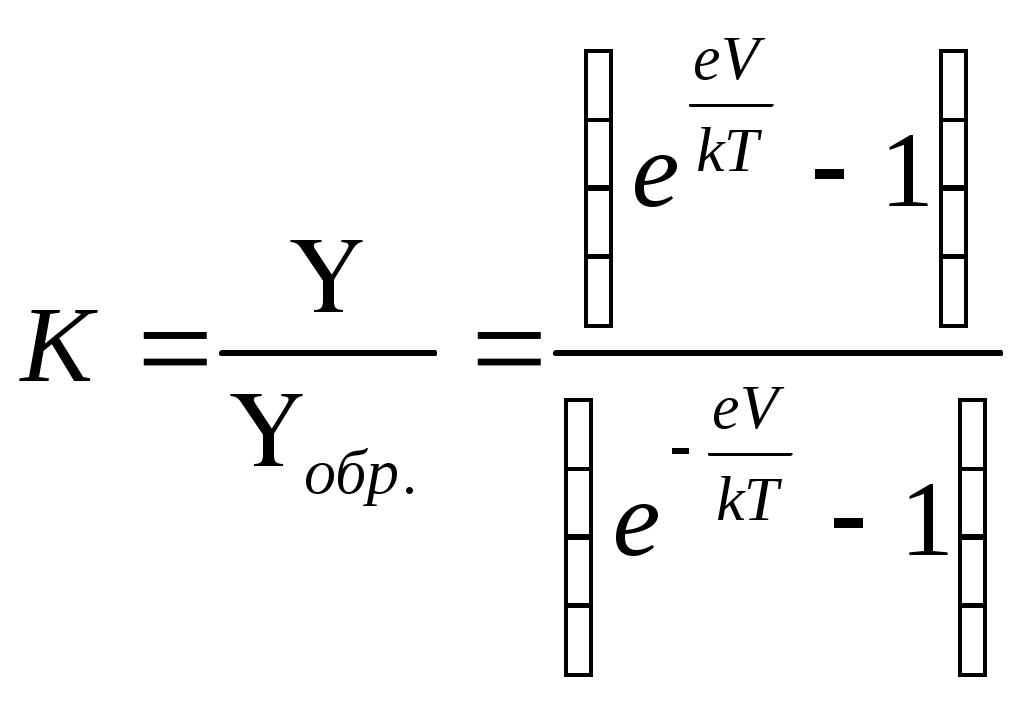 .
.
По условию задачи V = 0,2 В и T = 300 K, тогда 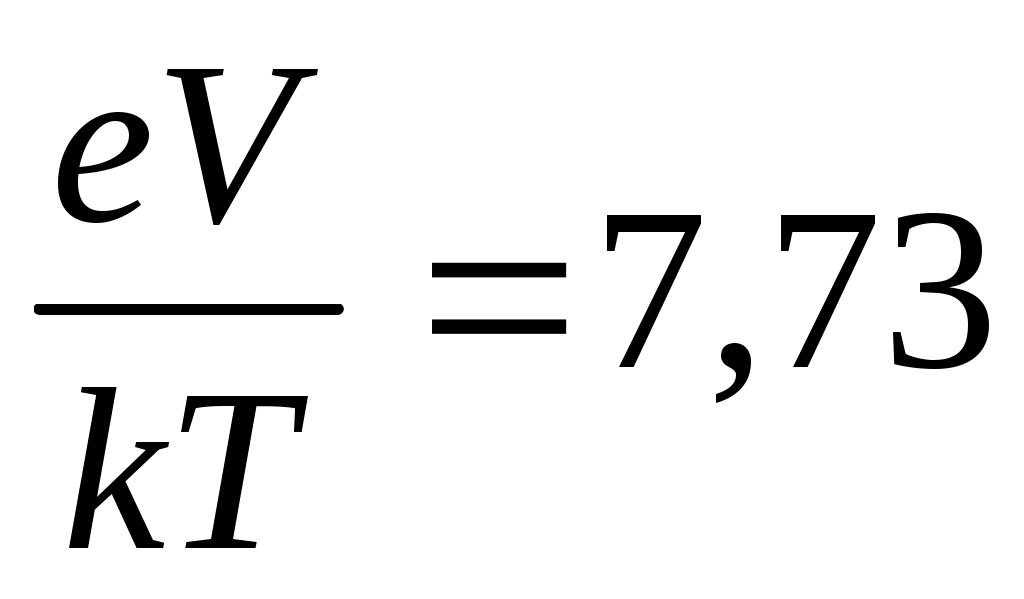 и
и
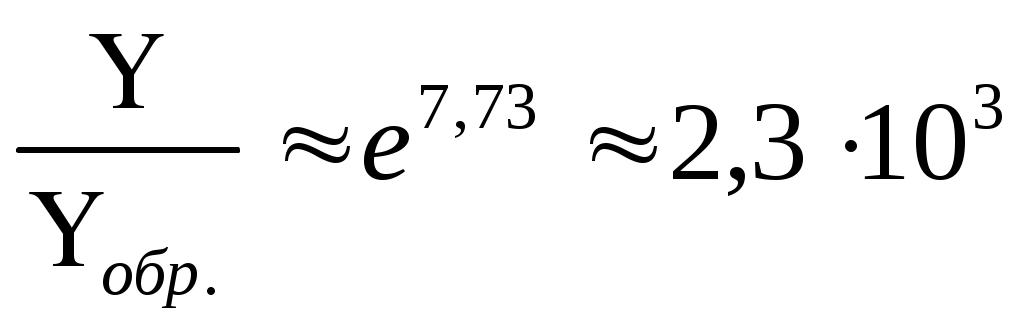 т.е. p – n - переход имеет высокий коэффициент выпрямления.
т.е. p – n - переход имеет высокий коэффициент выпрямления.
Задача 12*
Найти энергию Ферми для собственного полупроводника, принимая, что статистика Максвелла-Больцмана применима и для зоны проводимости, и для валентной зоны.
Решение
В любом полупроводнике равновесные концентрации электронов n0 (в зоне проводимости) и дырок p0 (в валентной зоне) можно записать в виде:
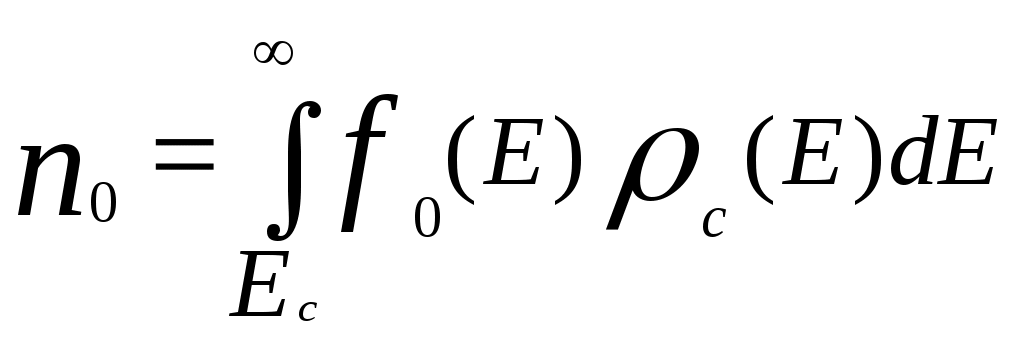
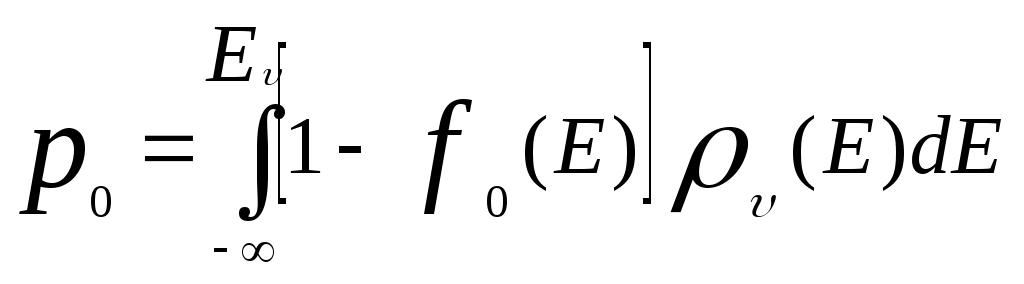 ,
,
где 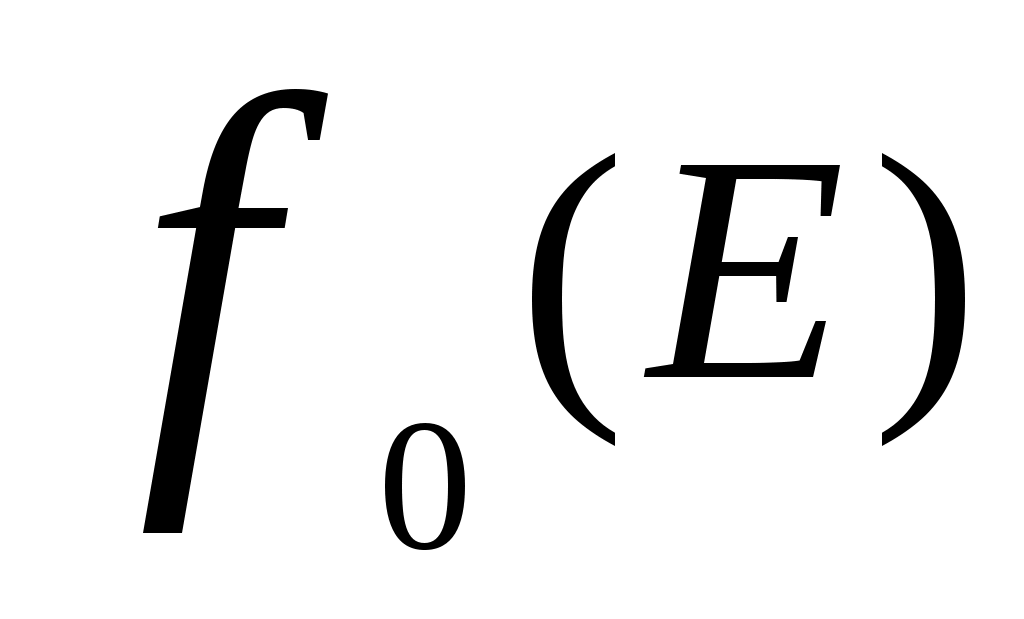 - функция распределения Ферми - Дирака
- функция распределения Ферми - Дирака
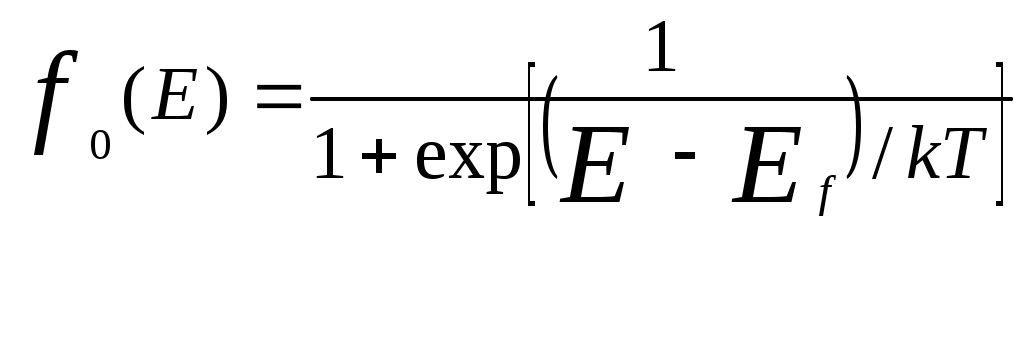 ,
,
где Ef - энергия Ферми, а функции плотности состояний с(E) для зоны проводимости и (E) для валентной зоны можно аппроксимировать функциями плотности состояний свободной частицы:
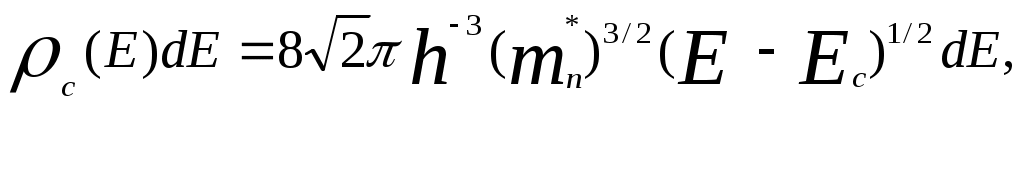
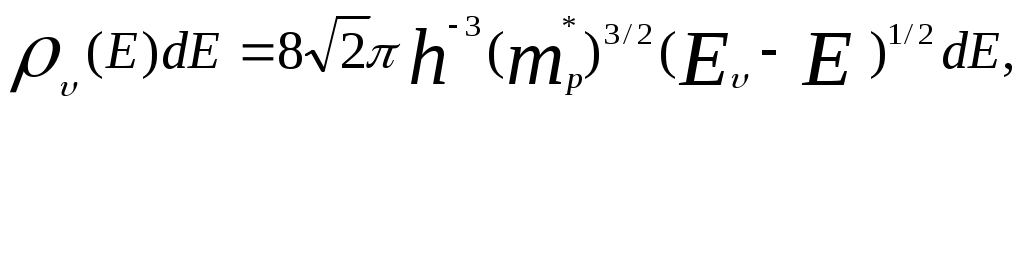
где mn* и mp* - эффективные массы электрона и дырки, Ec – энергия дна зоны проводимости, E - энергия потолка валентной зоны.
При интересующих нас температурах (
300 K)
по курсу «Физика твердого тела»
для студентов 2 курса
Модель свободных электронов металла
-
Ознакомьтесь с теоретическим материалом в курсе лекций
Лекция 4. Колебания кристаллической решетки
Лекция 5. Модель свободных электронов металла
Лекция 6. Зонная теория кристаллов. Полупроводники и диэлектрики
Лекция 7. Контактные явления ................................................ .................. https://edu.stankin.ru/mod/resource/view.php?id=338195
и в лекциях
Колоколов А.А. Избранные главы физики: конспект лекций / А.А.Колоколов. – М.: ФГБОУ ВПО МГТУ «СТАНКИН», 2015. – 89с.:ил.
https://edu.stankin.ru/mod/resource/view.php?id=336602
-
Ознакомьтесь с разбором и ходом решения задач
Задача №1
Условие
Концентрация электронов проводимости в германии при комнатной температуре n = 3·10 19 м-3. Плотность германия 5400 кг/м3, молярная масса германия 0,073 кг/моль. Каково отношение числа электронов проводимости к общему числу атомов?

Задача №2
Условие
По тонкой кремниевой пластинке шириной l = 3,2 мм и толщиной d = 250 мкм течет ток I = 5,2 мА. Кремний содержит примеси фосфора и является полупроводником n-типа. Число электронов в единице объема во много раз превышает концентрацию носителей заряда в чистом кремнии. Для данного образца концентрация электронов составляет nе = 1,5·10 23 м-3. Определите среднюю дрейфовую скорость электронов.

Задача №3
В цепь, состоящую из последовательно соединенных резистора с сопротивлением r = 1 кОм и термистора – полупроводникового прибора, электрическое сопротивление которого сильно зависит от температуры, включен источник постоянного тока. Температурная характеристика термистора приведена на рисунке.
 |
| |
Во сколько раз изменится сила тока I в цепи, если термистор, находившийся первоначально при комнатной температуре t1 = 20 °C, нагреть до 100 °C?
Решение
Сопротивление термистора при комнатной температуре t1 = 20 °C равно R1 = 13 кОм. При температуре t2 = 100 °C сопротивление термистора равно R2 = 2 кОм. Из закона Ома следует, что ток в цепи обратно пропорционален полному сопротивлению цепи. Таким образом,
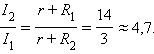
Задача №4
Условие
В усилителе, собранном на транзисторе по схеме с общей базой, сила тока в цепи эмиттера равна 12 мА, в цепи базы 600 мкА. Найти силу тока в цепи коллектора.
Решение
Сила тока в цепи коллектора будет равна разности сил тока в цепях эмиттера и базы:
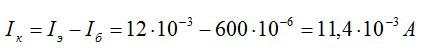
Ответ: 11,4 мА
Задача №5
Условие
Расстояние между катодом и анодом вакуумного диода равно 1 см. Сколько времени движется электрон от катода к аноду при анодном напряжении 440 В? Движение считать равноускоренным.
Решение
Начальную скорость электрона будем считать равной нулю. По закону сохранения энергии:
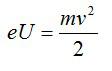
Отсюда выразим скорость:
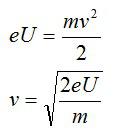
По 2 закону Ньютона, со стороны электрического поля на электрон действует сила, которая сообщает ему посоянное ускорение:
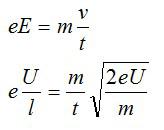
Выразим время и вычислим:
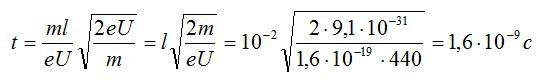
Ответ: 1,6 нс.
Задача №6
По тонкой кремниевой пластинке шириной l = 3,2 мм и толщиной d = 250 мкм течет ток I = 5,2 мА. Кремний содержит примеси фосфора и является полупроводником n-типа. Число электронов в единице объема во много раз превышает концентрацию носителей заряда в чистом кремнии. Для данного образца концентрация электронов составляет nе = 1,5·1023 м–3. Определите среднюю дрейфовую скорость
Решение
В примесных полупроводниках n-типа концентрация электронов во много раз превышает концентрацию дырок. Поэтому ток в полупроводниках n-типа практически полностью обусловлен дрейфом электронов под действием приложенного электрического поля.
Плотность тока j, т. е. сила тока, протекающего через единичное сечение образца, равна
Дрейфовая скорость электронов находится из выражения
где e – заряд электрона. Отсюда
Полученное значение дрейфовой скорости электронов в кремниевом полупроводнике n-типа на несколько порядков превышает дрейфовую скорость электронов в металлических проводниках.
Задача 7
Считая, что энергия Ферми для Na равна Ef=3,1 эВ и наблюдаемая электропроводность
=2,1107 Ом-1 м –1 при температуре Т = О К, рассчитать время релаксации (характерное время) .
Решение.
Время релаксации определим, преобразуя формулу Друде:
где - средняя длина свободного пробега электронов, f- скорость Ферми, N – плотность электронов проводимости.
Величину N получим, зная энергию Ферми. Поскольку для свободных электронов поверхность Ферми представляет собой сферу радиусом
а
энергия Ферми равна
Следовательно,
и
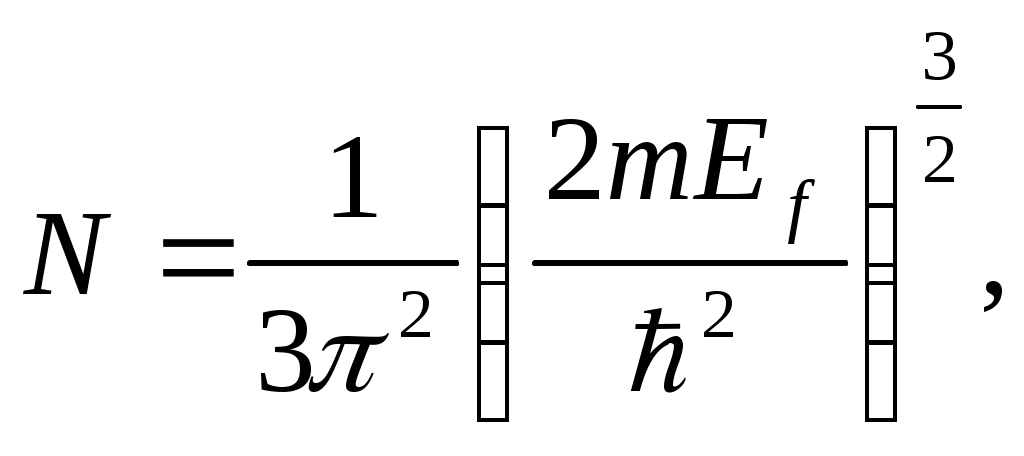
время релаксации равно
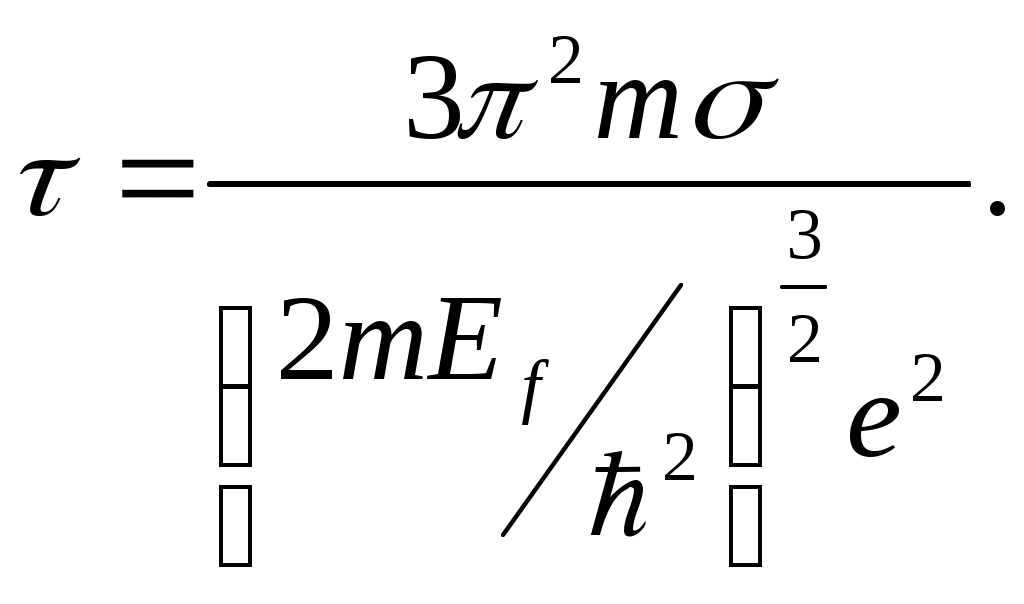
Подставляя значения получаем: = 310-14c.
Задача 8
Определить внутреннюю и внешнюю контактную разность потенциалов при комнатной температуре (
(E- Ef)/kT >> 1 для каждого значения энергии в зоне проводимости и (Ef-E)/kT >> 1 для каждого значения энергии в валентной зоне. Это значит, что для зоны проводимости (E > Ec):
а для валентной зоны:
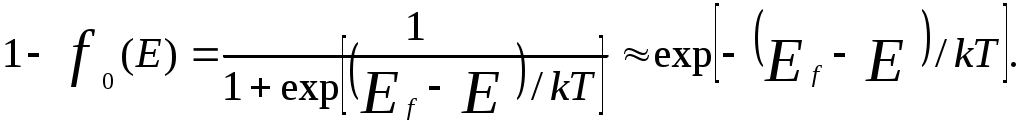
Последние выражения означают, что при описанных выше условиях распределение Ферми-Дирака электронов в зоне проводимости и дырок в валентной зоне можно аппроксимировать распределением Максвелла – Больцмана.
Вычислив интегралы, получим концентрацию электронов в зоне проводимости:
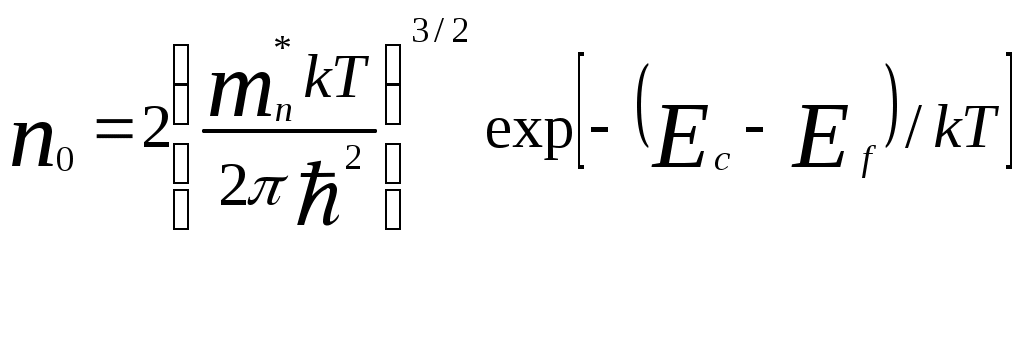
и концентрацию дырок в валентной зоне:
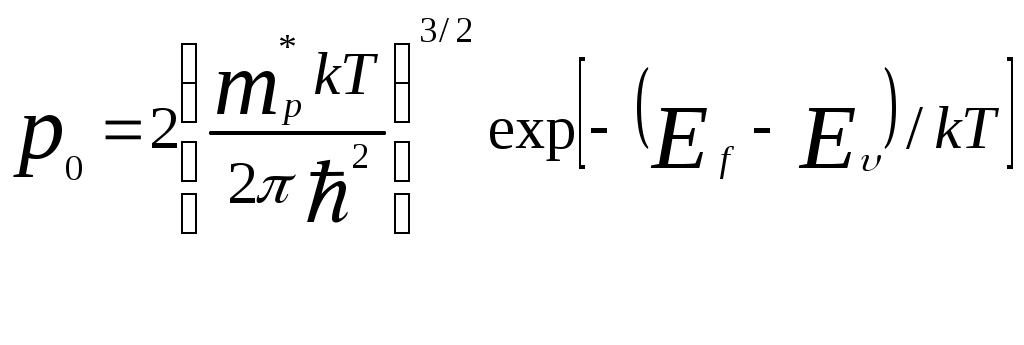
Для собственного полупроводника n0 = p0 = n. Приравняв правые части последних выражений, получаем:
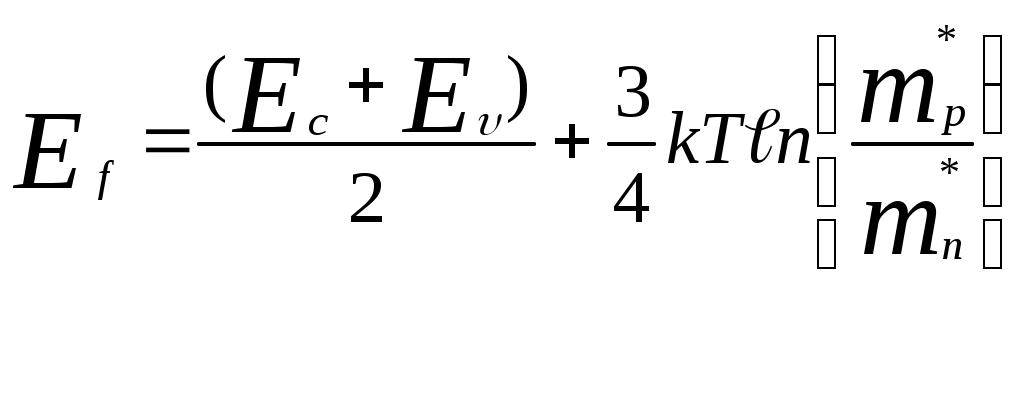
Отсюда ясно, что при mn* = mp* уровень Ферми лежит в запрещенной зоне посередине между краями зоны проводимости и валентной зоны; если mn* < mp* , то он смещается слегка вверх из этого положения, а если mn* > mp* , он смещается вниз.
-
Ознакомьтесь с разбором и ходом решения задач. Решите подобную задачу для своего варианта.
Условие
Найдите сопротивление полупроводникового диода в прямом и обратном направлениях тока, если при напряжении на диоде Uп=0,5 B сила тока равна Iп=5 мА, а при напряжении Uобр=10 B сила тока равна I обр= 0,1 мА.

Таблица 1 – Варианты заданий для решения Пример№1
| Вариант | Uп= В | Iп= мА | Uобр=B | I обр= мА |
| 1 | 0,1 | 1 | 5 | 0,05 |
| 2 | 0,2 | 2 | 6 | 0,06 |
| 3 | 0,3 | 3 | 7 | 0,07 |
| 4 | 0,25 | 4,5 | 8 | 0,08 |
| 5 | 0,4 | 4 | 9 | 0,09 |
| 6 | 0,5 | 5 | 10 | 0,1 |
| 7 | 0,6 | 6 | 11 | 0,11 |
| 8 | 0,7 | 7 | 12 | 0,12 |
| 9 | 0,8 | 8 | 13 | 0,13 |
| 10 | 0,9 | 9 | 14 | 0,14 |
| 11 | 1,0 | 10 | 15 | 0,15 |
| 12 | 1,1 | 11 | 16 | 0,16 |
| 13 | 1,2 | 12 | 17 | 0,17 |
| 14 | 1,3 | 13 | 18 | 0,18 |
| 15 | 1,4 | 14 | 19 | 0,19 |
| 16 | 1,5 | 15 | 20 | 0,20 |
| 17 | 1,6 | 16 | 21 | 0,21 |
| 18 | 1,7 | 17 | 22 | 0,22 |
| 19 | 1,8 | 18 | 23 | 0,23 |
| 20 | 1,9 | 1,9 | 24 | 0,24 |
-
Вопросы к практическому занятию:
Напишите конспективно ответы на вопросы:
Вопрос 1. Что такое полупроводник?
Вопрос 2. В чем отличие полупроводников от металлов?
Вопрос 3. Какой тип проводимости свойственен для полупроводников?
Вопрос 4. Что такое транзистор?
Вопрос 5. Что такое электронно-дырочный переход?