ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ “САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА”
Отчет по лабораторной работе №4
По курсу “Системы и сети массового обслуживания”
Тема:
“Замкнутые системы массового обслуживания”
Вариант №7
Выполнил:
студент группы
6131-090401
Проверил:
Есипов Б.А.
2022г.
Лабораторная работа №4
“ Замкнутые системы массового обслуживания ”
Вариант …
Исходное задание:
В состав оборудования вычислительного центра входит n независимо круглосуточно работающих ЭВМ.
Обслуживание ЭВМ производится группой из m специалистов. С учетом 8 часового рабочего дня при трехсменной работе приходится планировать всего 3m человек. Каждая ЭВМ может выйти из строя λ раз в месяц. Вышедшая из строя ЭВМ останавливается и , если в этот момент все специалисты заняты, становится в очередь на обслуживание и ждет пока любой из специалистов освободится. Среднее время ремонта tр известно. Убытки, связанные с одним часом простоя составляют N рублей. Месячная зарплата одного специалиста M рублей. Принять, что в месяце 30 рабочих дней
Определить, какое требуется количество специалистов в штате вычислительного центра, чтобы минимизировать месячные затраты S на обслуживание с учетом потерь от простоя ЭВМ. Объяснить, что для этого необходимо найти m, при которой обеспечивается
S = (ср. число неисправных ЭВМ) ∙ N∙(24час)∙(30дней) + 3m ⋅ M −>min
1.Изучить аналитические зависимости основных характеристик замкнутых СМО от параметров системы.
2. Используя формулы, написать программу расчета месячных затрат при изменяющемся количестве m и найти минимум.
3. Построить график S от m.
Задание 1. Изучить аналитические зависимости основных характеристик замкнутых СМО от параметров системы.
Задание 2. Используя формулы, написать программу расчета месячных затрат при изменяющемся количестве m и найти минимум.
Задание 3. Построить график S от m.
В варианте № параметры:
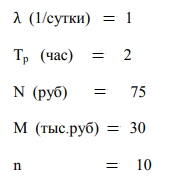
Решение:
Задание 1. Изучить аналитические зависимости основных характеристик замкнутых СМО от параметров системы.
Если работа источника заявок не зависит от состояния СМО, то такие СМО называются открытыми (разомкнутыми), т. е. это такие СМО, в которых заявки поступают извне. Если источник меняет свою работу в зависимости от состояния, СМО называется замкнутой (есть обратная связь).
Пример: Бригада из m рабочих обслуживает n станков (m
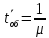 ,
,где µ – интенсивность потока обслуживаний.
Граф состояний для замкнутой СМО:
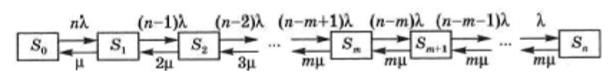
Рисунок 1 – Граф состояний для замкнутой СМО
Пусть λ - интенсивность потока неисправностей одного станка. Перечислим состояния:
S0 – все станки работают, рабочие свободны;
S1 – один станок неисправен, один рабочий его ремонтирует; ...
Sm – m станков неисправны, m рабочих их ремонтируют; ...
Sn – n станков неисправны, m станков ремонтируются, а (n-m) ожидают ремонта.
Видим, что это схема гибели и размножения.
Предельные вероятности состояний:
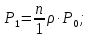
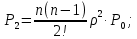
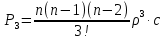
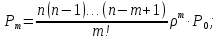
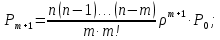
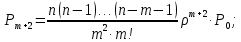
…
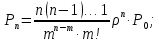
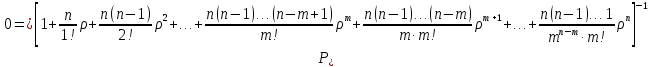
Вычислим среднее число занятых рабочих:
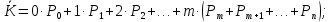
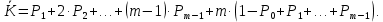
Среднее число неисправностей, обслуживаемое бригадой в единицу времени (абсолютная пропускная способность), получается как произведение среднего числа занятых рабочих на количество обслуживаемых заявок в единицу времени:
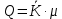
Среднее число неисправных станков – среднее число станков, связанных с процессом обслуживания:
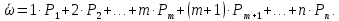
Эту величину можно подсчитать проще, если уже получена величина среднего числа занятых рабочих К.
Действительно, количество работающих станков (n-m). Эти работающие станки создают интенсивность потока неисправностей (n-m)λ. В стационарном режиме эти неисправности устраняются рабочими, которые устраняют Q неисправностей в единицу времени, значит:
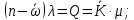
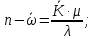
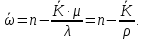
Среднее число станков, ожидающих в очереди:
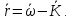
Задание 2. Используя формулы, написать программу расчета месячных затрат при изменяющемся количестве m и найти минимум.
В качестве программного обеспечения для выполнения данной лабораторной работы был выбран пакет MachCad версии 13, так как это удобный программный продукт для алгоритмических вычислений, который позволяет автоматизировать сложные математические расчёты. Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически, в противовес текстовой записи в языках программирования, что позволяет проводить более наглядные вычисления. Листинг программы представлен в конце отчёта.
Результат работы программы:
При m = 1 месячные затраты S равны = 522000
При m = 2 месячные затраты
S равны = 506000
При m = 3 месячные затраты S равны = 512600
При m = 4 месячные затраты S равны = 560600
При m = 5 месячные затраты S равны = 635400
При m = 6 месячные затраты S равны = 721100
При m = 7 месячные затраты S равны = 810200
При m = 8 месячные затраты S равны = 900000
При m = 9 месячные затраты S равны = 990000
При m = 10 месячные затраты S равны = 1080000
Исходя из полученных вычислений видно, что минимальные затраты достигаются при включении в процесс двух ремонтников.
Задание 3. Построить график S от m.
На графике видны вычисления при каждом m, а также показана зависимость месячных затрат от числа ремонтников. Ось X – число ремонтников, а ось Y – месячные затраты. Сам график был сформирован с помощью Microsoft Excel (рисунок 1).
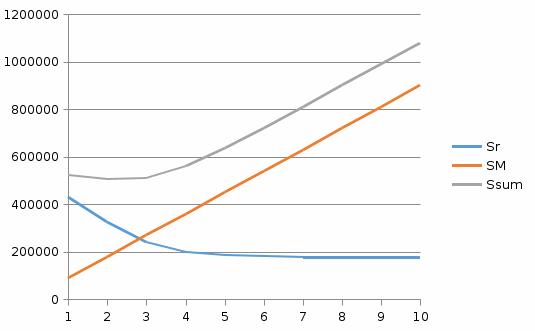
Рисунок 1 – результат вычислений
На рисунке 1 Sr – затраты от поломок станков, SM – затраты на зарплату ремонтников, а Ssum – общие затраты.
Вывод:
При выполнении лабораторной работы с помощью программы MathCad 13 были произведены вычисления минимальных затрат замкнутой системы массового обслуживания, после чего в программе Microsoft Excel был сформирован график зависимости S от m. В результате выяснилось, что минимальных затрат можно достичь, если нанять двух ремонтников.
Листинг программы(рисунок 2-12).
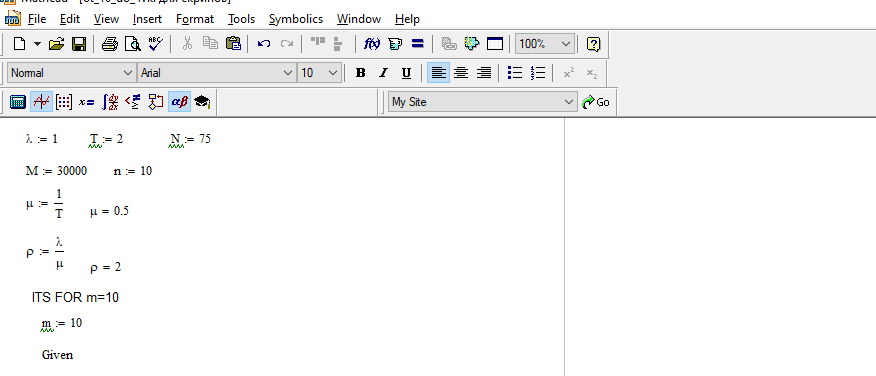
Рисунок 2 – исходные данные
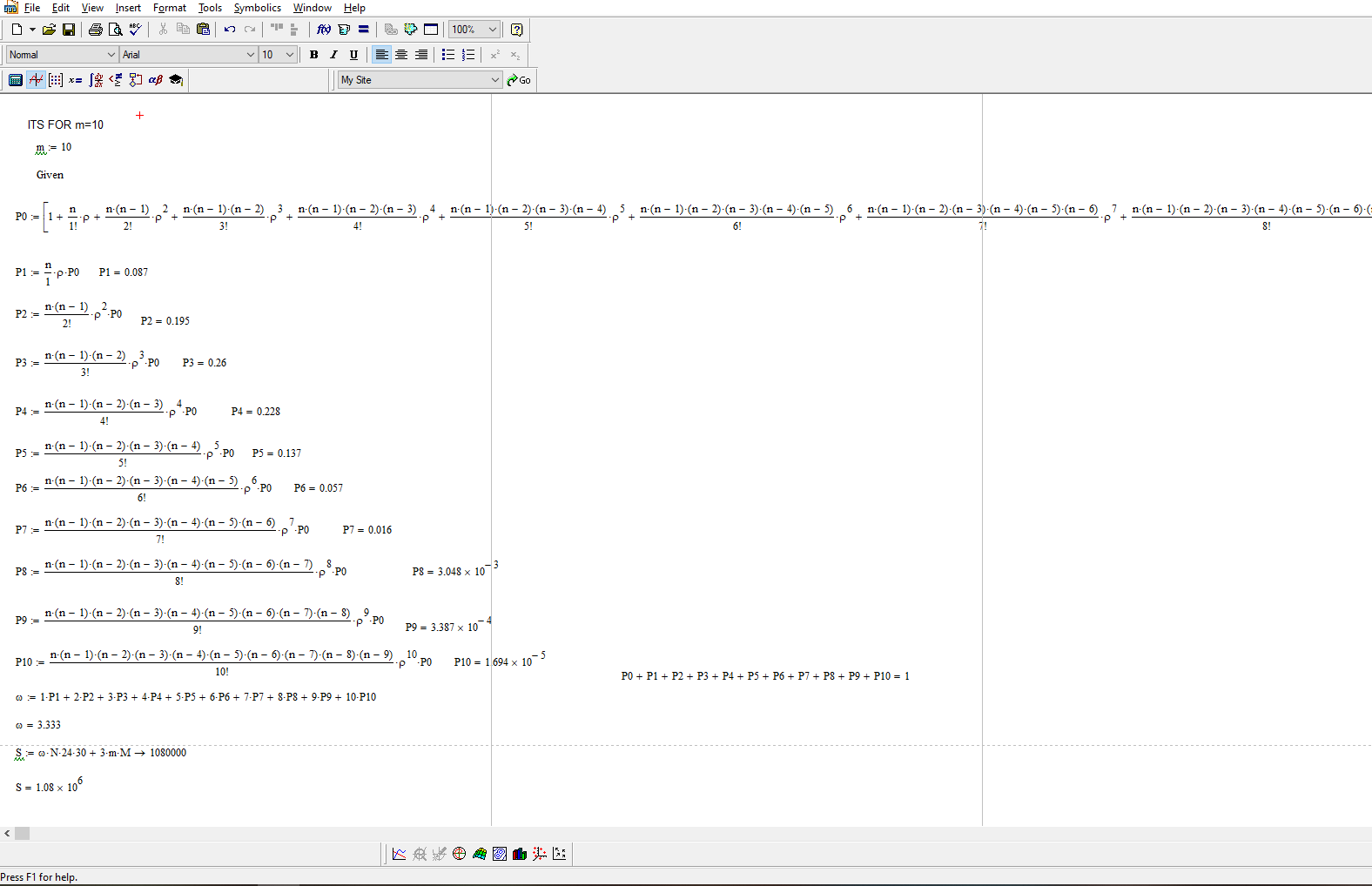
Рисунок 3 – при m=10
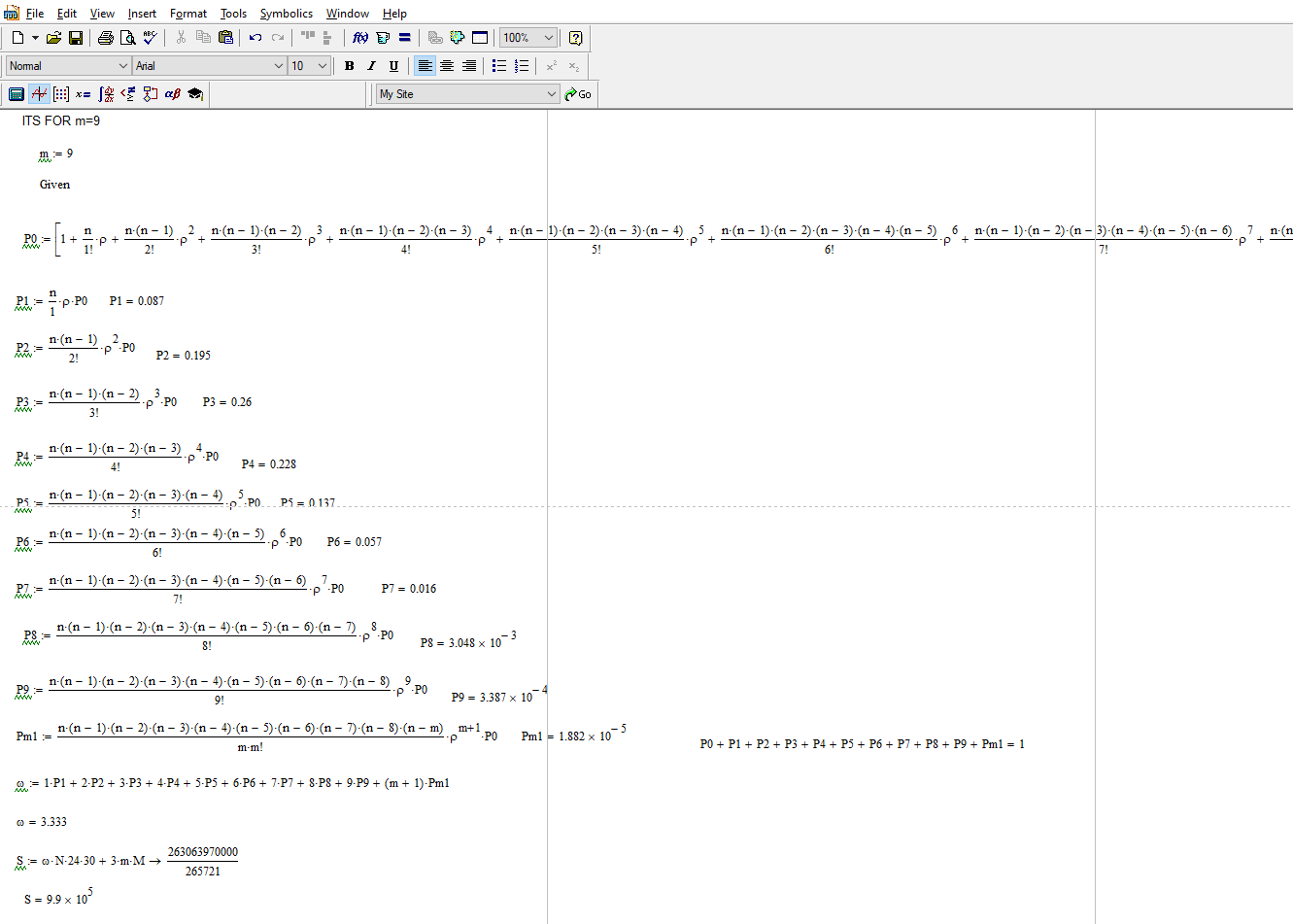
Рисунок 4 – при m=9
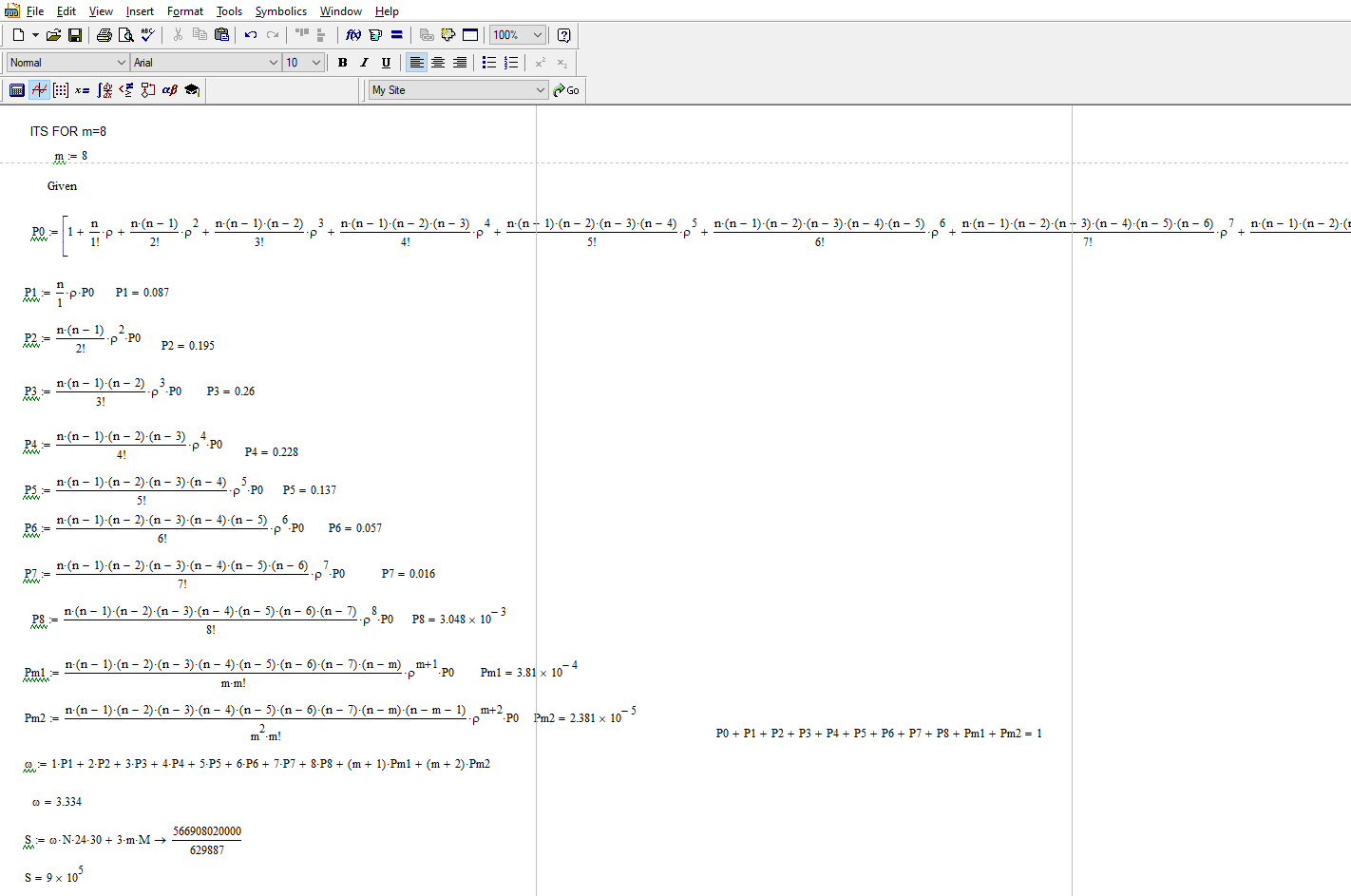
Рисунок 5 – при m=8
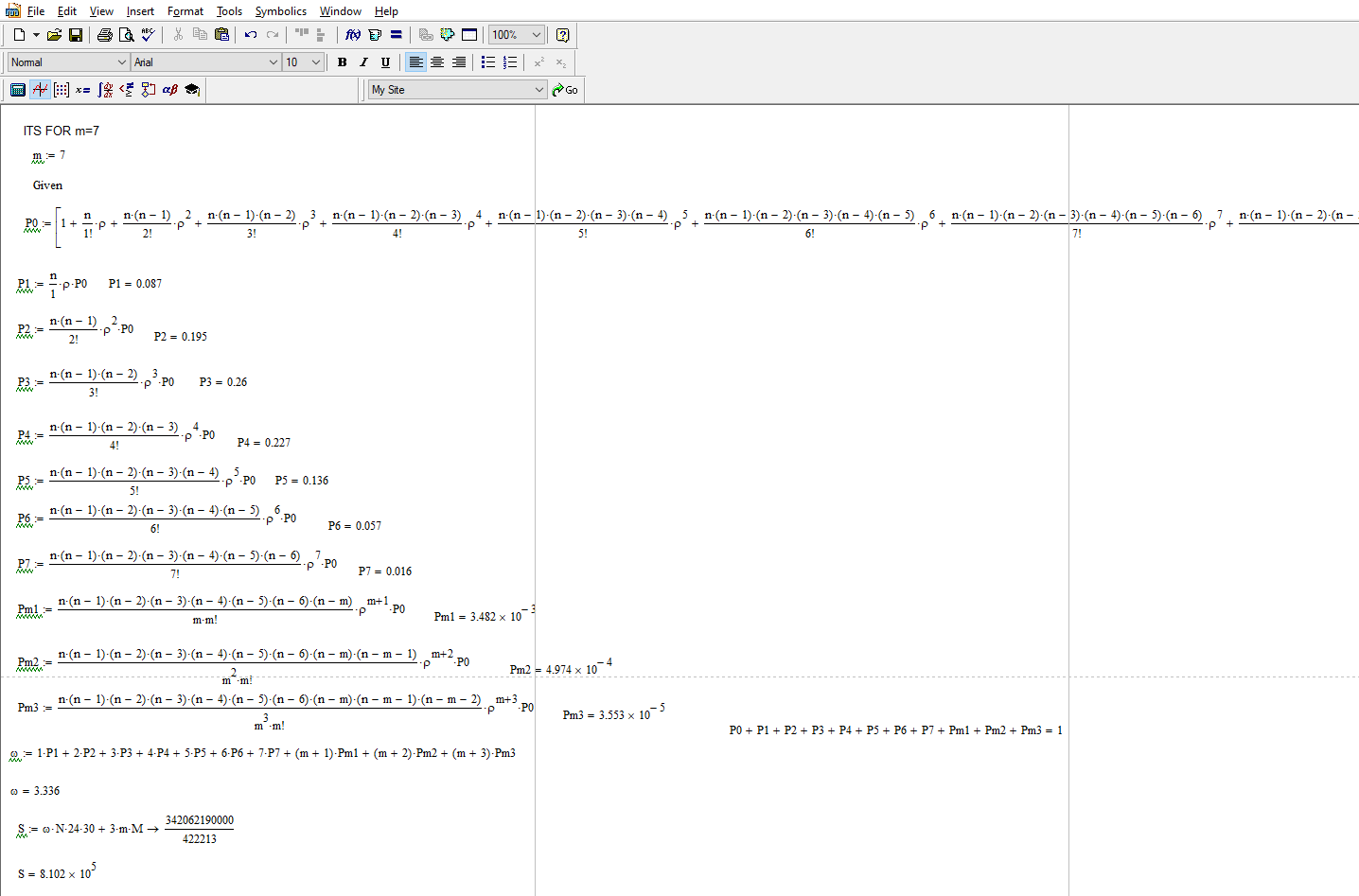
Рисунок 6 – при m=7
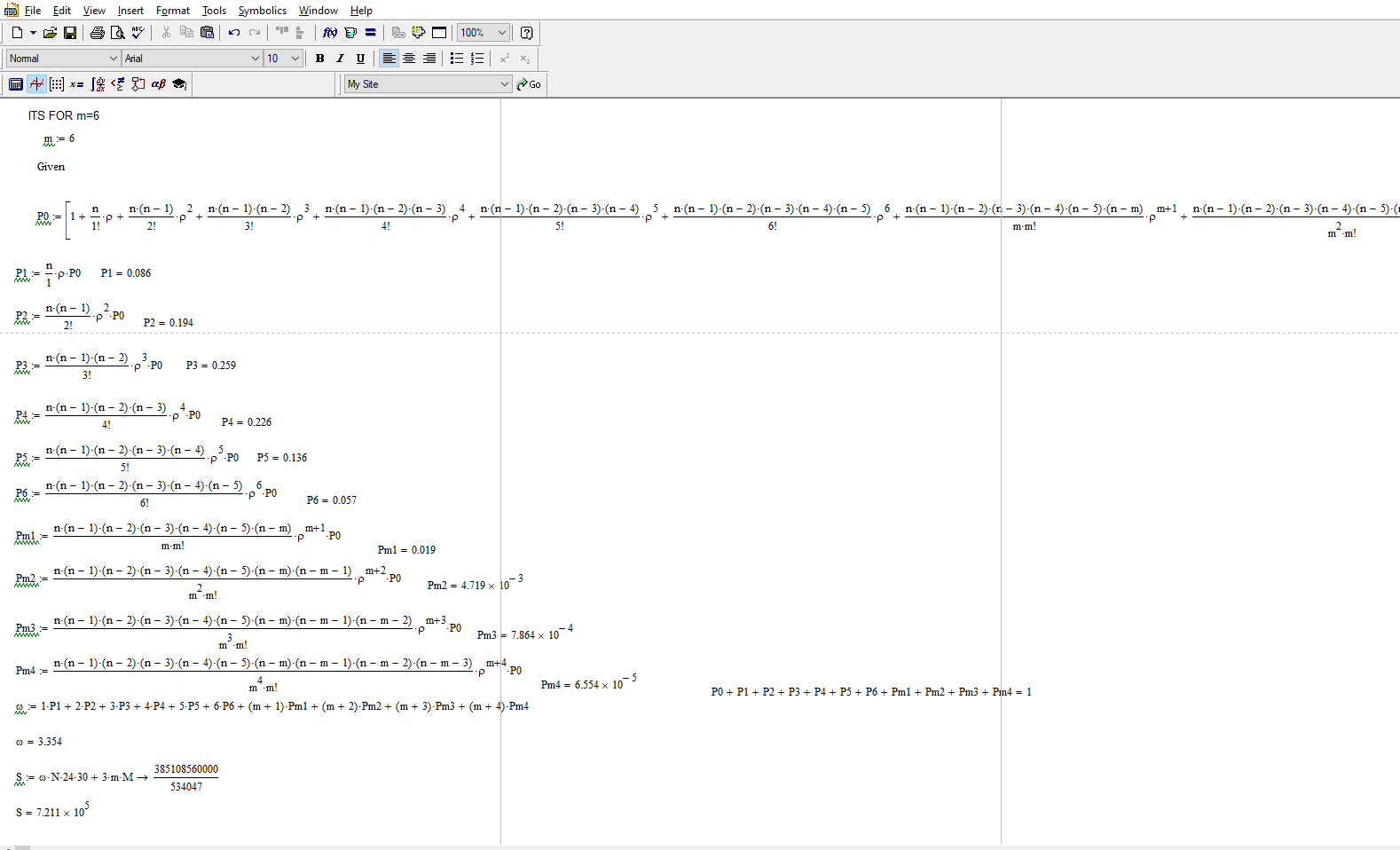
Рисунок 7 – при m=6
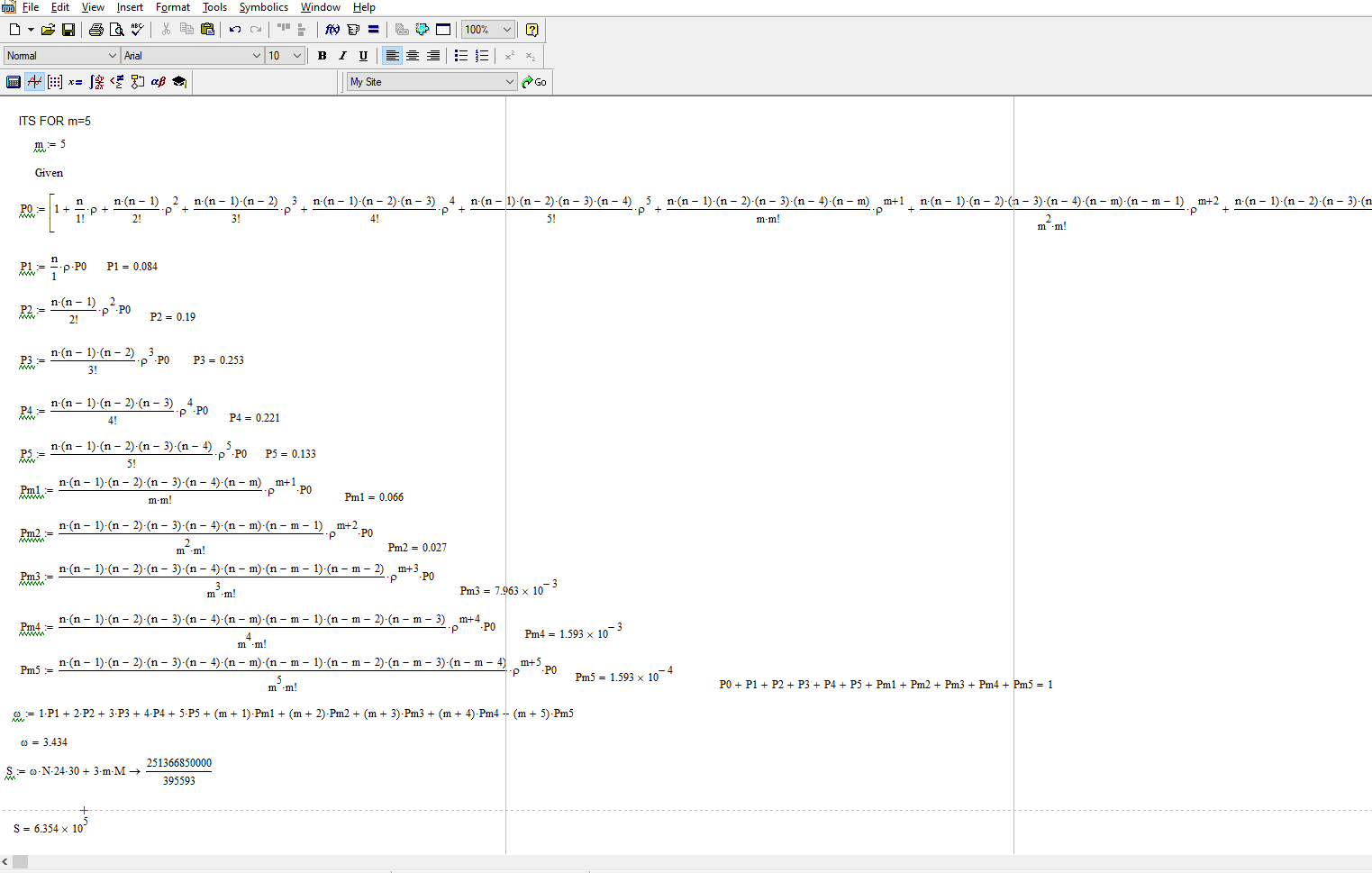
Рисунок 8 – при m=5
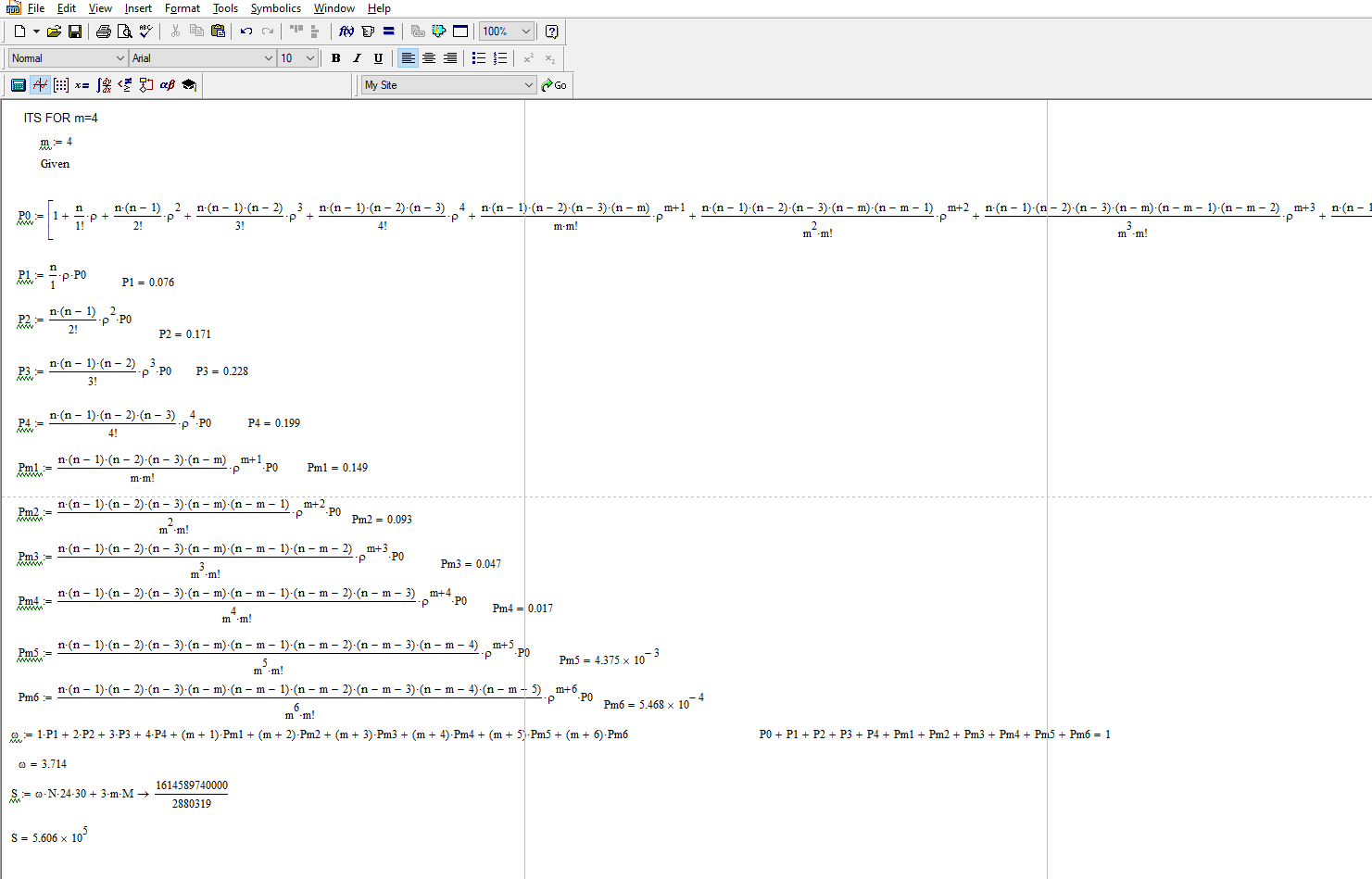
Рисунок 9 – при m=4
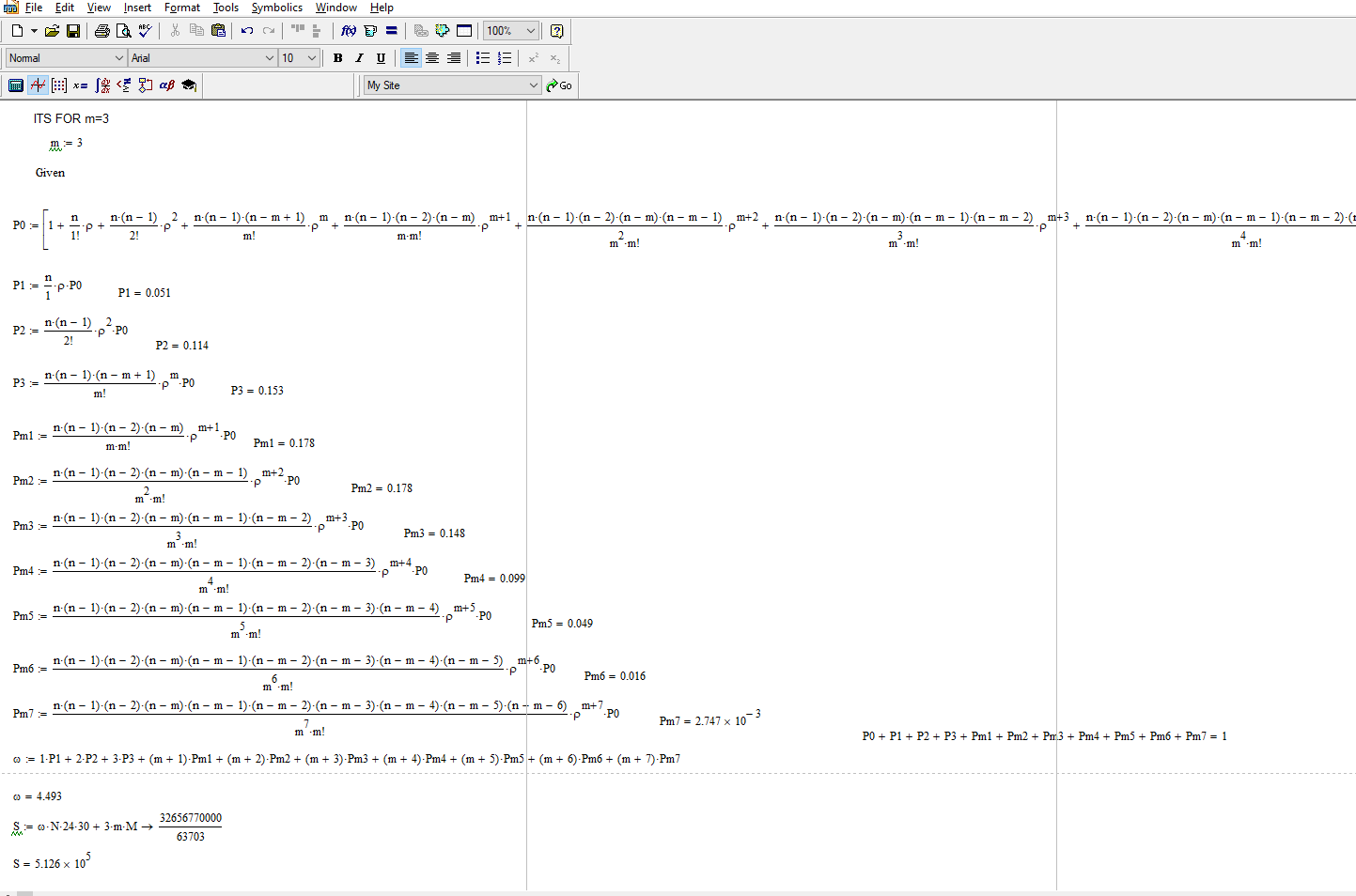
Рисунок 10 – при m=3
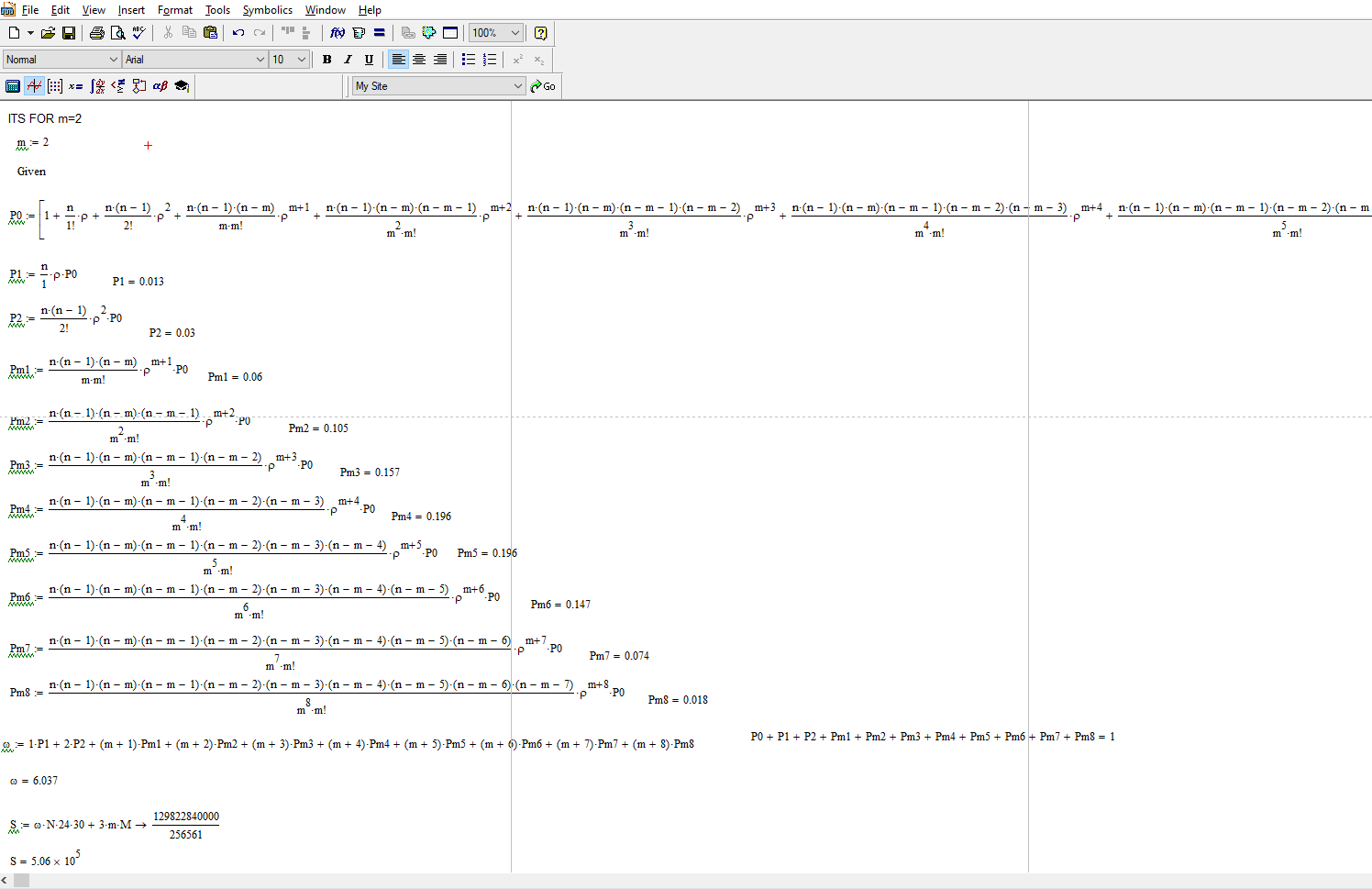
Рисунок 11 – при m=2
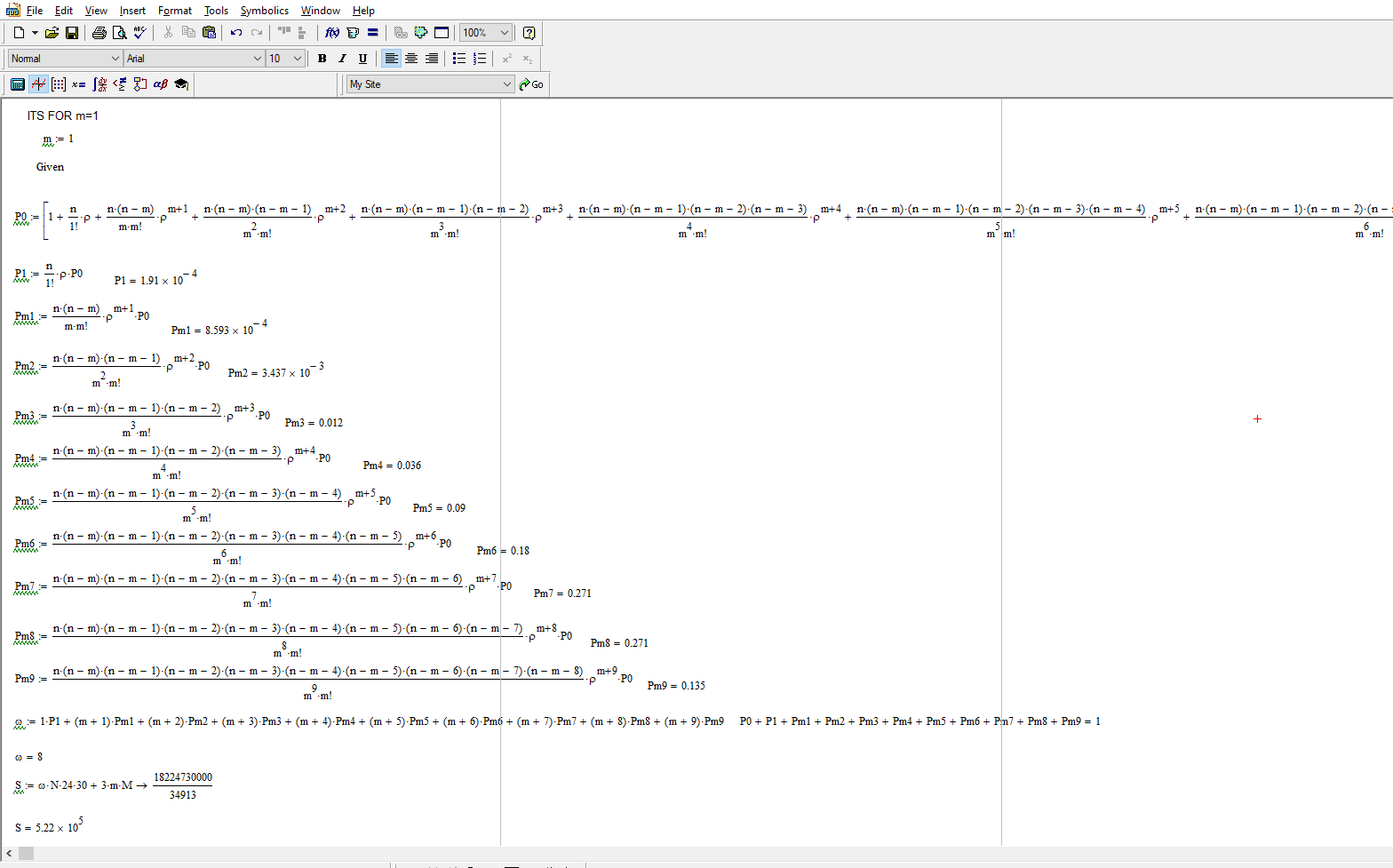
Рисунок 12 – при m=1