ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 167
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, вставленный в выходной патрубок ВП. Между наружной поверхностью дросселя Д и внутренней поверхностью патрубка ВП образуется кольцевой зазор необходимого размера. Верхний обрез дросселя имеет вид конического раструба и размещается непосредственно под входным отверстием бака.
При пуске насосного агрегата вода откачивается из бака, поступая в насос через кольцевой зазор между дросселем и входным патрубком аккумулятора. Благодаря эжекторному эффекту кольцевого зазора, вместе с водой откачивается и воздух, который поступает в насос из верхней части бака по дроссельной трубе. После того как в верхней части бака создано необходимое разрежение, вода по всасывающему трубопроводу поднимается в бак и, пройдя дроссельную трубу, поступает в насос. При помощи уравнительной трубки УТ обеспечивается выравнивание давлений в верхней части бака и всасывающей полости насоса, что повышает надежность пуска насосного агрегата.
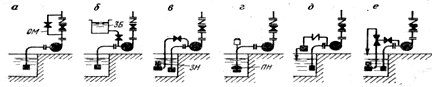
Рис. 6.27. Схемы заливки главных насосов водоотливных установок
Воздух, накапливаемый в нагнетательном трубопроводе в процессе пуска насоса, выпускается в атмосферу при помощи вантуза, который устанавливают перед обратным клапаном.
На зумпфовых водоотливных установках с насосными станциями, расположенными над уровнем воды в водосборнике, используют следующие способы заливки лопастных насосов перед пуском (рис.6.27):
Первые три способа заливки из перечисленных выше возможны только в том случае, когда на входе во всасывающий трубопровод заполняемого насоса установлен обратный клапан. Следует иметь в виду, что обратные клапаны всасывающих трубопроводов обладают значительным, сопротивлением и при низкой кавитационной стойкости насосов существенно понижают их допустимую высоту всасывания. Кроме того, обратные клапаны постепенно теряют герметичность из-за износа уплотнительных элементов и засорения. Схемы заливки с использованием подпиточных насосов, вакуум-насосов и эжекторов не требуют установки обратного клапана на всасывающих трубопроводах. Все перечисленные способы заливки могут быть автоматизированными.
ТЕОРЕТИЧЕСКИЙ И ДЕЙСТВИТЕЛЬНЫЙ РАБОЧИЕ ЦИКЛЫ ПОРШНЕВОГО НАСОСА. НЕРАВНОМЕРНОСТЬ ПОДАЧИ ВОЗВРАТНО ПОСТУПАТЕЛЬНЫХ НАСОСОВ
Теоретический и действительный рабочие циклы поршневого насоса.
Процесс преобразования энергии в поршневом насосе характеризуется значительным изменением давления при прохождении жидкости через цилиндр и в меньшей степени - изменением кинетической энергии. Поэтому при исследовании баланса энергии в поршневых машинах пользуются индикаторными диаграммами их рабочих циклов
, которые представляют зависимость давления Рц жидкости в цилиндре от объема V, описываемого поршнем.
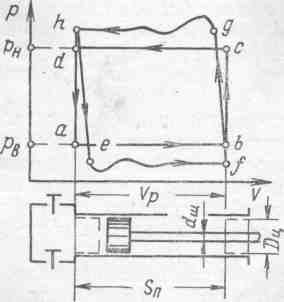
Рис. 6.28. Индикаторные диаграммы рабочего цикла поршневого насоса.
Допустим, что в идеальном случае жидкость, перекачиваемая насосом, практически несжимаема, отсутствуют ее утечки через неплотноcть рабочей камеры и кроме того, клапаны насоса безынерционны, а гидравлическое сопротивление их проточных каналов бесконечно мало. Тогда индикаторная диаграмма рабочего цикла насоса будет иметь вид прямоугольника abcd (рис.6.28): линия ab отражает процесс поступления жидкости в цилиндр при постоянном давлении, равном давлению во всасывающем патрубке; bc -мгновенное увеличение давления в момент начала вытеснения жидкости, когда закрывается всасывающий и открывается нагнетательный клапаны; cd - процесс вытеснения жидкости из цилиндра в нагнетательный патрубок; da - обратная смена клапанов в момент начала очередного цикла.
В координатной плоскости рV любая площадь имеет размерность работы (энергии). Площадь индикаторной диаграммы численно равна энергии, расходуемой за цикл на перемещение жидкости из области низкого в область высокого давления.
Как видно из рис. 6.28, в идеальном случае расход энергии Е (Н*м) за цикл определяется следующим образом:
E=pVp (6.29)
где: р = рн-рв - давление насоса, Па
рн и рв - соответственно давление в нагнетательном и всасывающем патрубках, Па
Vр - объем, описываемый поршнем за цикл (рабочий объем цилиндра), м3.
Рабочий объем цилиндра Vp в идеальном случае равен расходу жидкости за цикл. При известных продолжительности цикла tц и количестве цилиндров Zц в насосе его теоретическая производительноcть (м3/с).
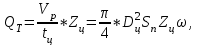(6.30)
Где: ω=1/tц частота вращения коленчатого вала, об/с
Dс и Sn соответственно диаметр цилиндра и ход поршня насоса, м.
Если насосы имеют цилиндры двойного действия, то их теоретическая производительность:
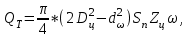(6.31)
где: dω - диаметр штока, м.
Индикаторная диаграмма (см.рис.6.28) действительного рабочего цикла насоса отличается от теоретической из-за ряда причин. Сопротивление всасывающего и нагнетательного трактов приводят к понижению давления в цилиндре при всасывании и его повышению при нагнетании по сравнению с соответствующими давлениями в наружных патрубках. Процессы ef и нагнетания gh нелинейны вследствие инерционности клапанов и вибраций их запорных элементов, а также из-за изменяющегося во времени расхода жидкости через проточные каналы всасывающего и нагнетательного трактов.
Реальные жидкости сжимаемы, что объясняется в основном наличием в связи с этим линии повышения fg и понижения he давлений не вертикальны, а наклонны. Кроме того, на форму линий и существенное влияние оказывают негерметичность цилиндра и клапанов, а также запаздывание в срабатывании последних.
Действительная индикаторная диаграмма определяется опытным путем с помощью самопишущего манометра - индикатора. Помимо рассмотренных выше причин, форма диаграммы реального цикла в значительной степени зависит от эксплуатационного состояния рабочих узлов цилиндра насоса.
Как видно из рис. 6.28, в момент начала очередного процесса всасывания жидкость, оставшаяся в мертвом пространстве клапанной коробки, расширяется и занимает часть рабочего объема цилиндра, обуславливая уменьшение производительности насоса. Общее понижение действительной производительности по сравнению с теоретической из-за влияния сжимаемости жидкости, а также внутренних перетоков через клапаны внешних утечек, оценивается объемным коэффициентом полезного действия
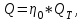(6.32)
где: Q - действительная производительность насоса, м3/с
η = 0,8-0,95 - его объемный к.п.д. (насосы большей производительности имеют, как правило, и более высокий к.п.д.).
Как видно из формул теоретическая производительность насоса целиком определяется его конструктивными параметрами и не зависит от давления жидкости. Поэтому поршневые насосы имеют жесткую по расходу напорную характеристику.
Полный к.п.д. насоса определяется следующим образом:
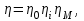(6.33)
где: ηi- индикаторный к.п.д., определяемый как отношение площади теоретической и действительной индикаторных диаграмм,
ηМ - механический к.п.д., учитывающий потери энергии на трение в поршневой группе насоса.
Индикаторная диаграмма позволяет, помимо энергетических параметров насоса, оценивать величины сопротивлений всасывающего и нагнетательного клапанов, а также индицировать внутренние неисправности в цилиндре.
Неравномерность подачи возвратно – поступательных насосов.
Использование кривошипно—шатунного механизма в приводе обуславливает изменение скорости движения поршня и подачи жидкости в течение рабочего цикла поршневых и плунжерных насосов.
Пусть на схеме (рис.6.28) точка К отображает крайнее левое положение ползуна в направляющих, а х - линейное перемещение пoлзуна при повороте кривошипа на угол φ.
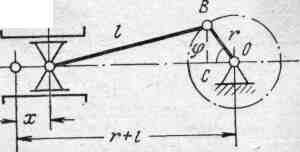
Рис. 6.28. Схема кривошипно-шатунного механизма поршневого насоса.
По-видимому, линейные перемещения ползуна и поршня одинаковы в любой момент времени и определяются следующим образом:
х=КО-АО, х=(1-cos φ)+l(1-cosβ) (6.34)
где: l – длина шатуна,
β – угол наклона шатуна к оси перемещения ползуна,
r – радиус кривошипа.
Из треугольников ABC и ВОС имеем sinβ=r/l*sin φ
Тогда:
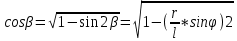(6.35)
Разложив последний радикал по формуле бинома Ньютона и отбросив третье и последующие слагаемые как малые величины высших порядков, приближенно получим:
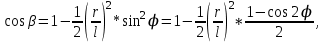(6.36)
Линейное перемещение ползуна:
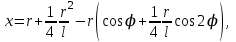(6.37)
В кривошипно-шатунных механизмах поршневых насосов обычно принимают r/l =1/5 = 0,2. Если пренебречь вторым слагаемым разложения, которое при максимальной величине = 1 не превышает 0,02, то (6.37) упростится и преобразуется в следующее:
x=r(1-cos φ)=r(1-cos2πωt), (6.38)
где: ω - частота вращения коленчатого вала, об/с,
t - отрезок времени, в течение которого кривошип поворачивав на угол φ относительно оси перемещения ползуна, с.
С учетом (6.38) линейная скорость ползуна (поршня)
Vп=dx/dt=2πωrsin2πωt, (6.39)
а величина линейного ускорения:
ωп=dVn/dt=4π2 ω2 r cos2πωt. (6.40)
Как видно из уравнений (6.39) и (6.40), линейная скорость поршня в пределах цикла изменяется по закону синуса, а ускорение по закону косинуса. Скорость Vn достигает максимальной величины при φ = 90° и φ = 270°, а ускорение - при φ = 0 и φ = 180°, когда поршень находится в крайних положениях.
Если скорость Vn определить с учетом более точного исходного уравнения (6.37) и допустить, что r/l = 0,2, тс ее максимальная величина:
Vмах=4π2 ω2 r(1± r/l), (6.41)
достигается при φ =80°, а максимальное значение ускорения:
ωмах=4π2 ω2 r(1± r/l), (6.42)
где знак плюс относится к крайнему левому положению поршня, а минус - к правому.
В нормально работающем насосе жидкость безотрывно следует за поршнем. При постоянном поперечном сечении поршня текущее значение подачи жидкости будет:
Qt=Fn Vn=2πωrFn sin2πωt, (6.43)
Как видно из рис.6.29, подача одноцилиндрового насоса простого действия в течение его рабочего цикла характеризуется крайней неравномерностью.
При пуске насосного агрегата вода откачивается из бака, поступая в насос через кольцевой зазор между дросселем и входным патрубком аккумулятора. Благодаря эжекторному эффекту кольцевого зазора, вместе с водой откачивается и воздух, который поступает в насос из верхней части бака по дроссельной трубе. После того как в верхней части бака создано необходимое разрежение, вода по всасывающему трубопроводу поднимается в бак и, пройдя дроссельную трубу, поступает в насос. При помощи уравнительной трубки УТ обеспечивается выравнивание давлений в верхней части бака и всасывающей полости насоса, что повышает надежность пуска насосного агрегата.
Рис. 6.27. Схемы заливки главных насосов водоотливных установок
Воздух, накапливаемый в нагнетательном трубопроводе в процессе пуска насоса, выпускается в атмосферу при помощи вантуза, который устанавливают перед обратным клапаном.
На зумпфовых водоотливных установках с насосными станциями, расположенными над уровнем воды в водосборнике, используют следующие способы заливки лопастных насосов перед пуском (рис.6.27):
-
перепуском воды из нагнетательного става а насос по обводным магистралям ОМ (рис. 6.27, а), снабженным перепускными вентилями; -
подводом воды из заливочного бака ЗБ (рис. 6.27, б) или водоема, расположенного выше горизонта установки насосав; -
специальным погружным или самовсасывающим заливочным насосом ЗН (рис 6.27, в); -
подпиточным погружным насосом ПН (рис 6.27, г); -
вакуум—насосным агрегатом (рис. 6.27, д); -
при помощи эжекторной установки (рис. 6.27, е), силовым агрегатом которой является погружной или самовсасывающий насос.
Первые три способа заливки из перечисленных выше возможны только в том случае, когда на входе во всасывающий трубопровод заполняемого насоса установлен обратный клапан. Следует иметь в виду, что обратные клапаны всасывающих трубопроводов обладают значительным, сопротивлением и при низкой кавитационной стойкости насосов существенно понижают их допустимую высоту всасывания. Кроме того, обратные клапаны постепенно теряют герметичность из-за износа уплотнительных элементов и засорения. Схемы заливки с использованием подпиточных насосов, вакуум-насосов и эжекторов не требуют установки обратного клапана на всасывающих трубопроводах. Все перечисленные способы заливки могут быть автоматизированными.
ТЕОРЕТИЧЕСКИЙ И ДЕЙСТВИТЕЛЬНЫЙ РАБОЧИЕ ЦИКЛЫ ПОРШНЕВОГО НАСОСА. НЕРАВНОМЕРНОСТЬ ПОДАЧИ ВОЗВРАТНО ПОСТУПАТЕЛЬНЫХ НАСОСОВ
Теоретический и действительный рабочие циклы поршневого насоса.
Процесс преобразования энергии в поршневом насосе характеризуется значительным изменением давления при прохождении жидкости через цилиндр и в меньшей степени - изменением кинетической энергии. Поэтому при исследовании баланса энергии в поршневых машинах пользуются индикаторными диаграммами их рабочих циклов
, которые представляют зависимость давления Рц жидкости в цилиндре от объема V, описываемого поршнем.
Рис. 6.28. Индикаторные диаграммы рабочего цикла поршневого насоса.
Допустим, что в идеальном случае жидкость, перекачиваемая насосом, практически несжимаема, отсутствуют ее утечки через неплотноcть рабочей камеры и кроме того, клапаны насоса безынерционны, а гидравлическое сопротивление их проточных каналов бесконечно мало. Тогда индикаторная диаграмма рабочего цикла насоса будет иметь вид прямоугольника abcd (рис.6.28): линия ab отражает процесс поступления жидкости в цилиндр при постоянном давлении, равном давлению во всасывающем патрубке; bc -мгновенное увеличение давления в момент начала вытеснения жидкости, когда закрывается всасывающий и открывается нагнетательный клапаны; cd - процесс вытеснения жидкости из цилиндра в нагнетательный патрубок; da - обратная смена клапанов в момент начала очередного цикла.
В координатной плоскости рV любая площадь имеет размерность работы (энергии). Площадь индикаторной диаграммы численно равна энергии, расходуемой за цикл на перемещение жидкости из области низкого в область высокого давления.
Как видно из рис. 6.28, в идеальном случае расход энергии Е (Н*м) за цикл определяется следующим образом:
E=pVp (6.29)
где: р = рн-рв - давление насоса, Па
рн и рв - соответственно давление в нагнетательном и всасывающем патрубках, Па
Vр - объем, описываемый поршнем за цикл (рабочий объем цилиндра), м3.
Рабочий объем цилиндра Vp в идеальном случае равен расходу жидкости за цикл. При известных продолжительности цикла tц и количестве цилиндров Zц в насосе его теоретическая производительноcть (м3/с).
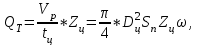(6.30)Где: ω=1/tц частота вращения коленчатого вала, об/с
Dс и Sn соответственно диаметр цилиндра и ход поршня насоса, м.
Если насосы имеют цилиндры двойного действия, то их теоретическая производительность:
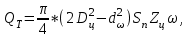(6.31)где: dω - диаметр штока, м.
Индикаторная диаграмма (см.рис.6.28) действительного рабочего цикла насоса отличается от теоретической из-за ряда причин. Сопротивление всасывающего и нагнетательного трактов приводят к понижению давления в цилиндре при всасывании и его повышению при нагнетании по сравнению с соответствующими давлениями в наружных патрубках. Процессы ef и нагнетания gh нелинейны вследствие инерционности клапанов и вибраций их запорных элементов, а также из-за изменяющегося во времени расхода жидкости через проточные каналы всасывающего и нагнетательного трактов.
Реальные жидкости сжимаемы, что объясняется в основном наличием в связи с этим линии повышения fg и понижения he давлений не вертикальны, а наклонны. Кроме того, на форму линий и существенное влияние оказывают негерметичность цилиндра и клапанов, а также запаздывание в срабатывании последних.
Действительная индикаторная диаграмма определяется опытным путем с помощью самопишущего манометра - индикатора. Помимо рассмотренных выше причин, форма диаграммы реального цикла в значительной степени зависит от эксплуатационного состояния рабочих узлов цилиндра насоса.
Как видно из рис. 6.28, в момент начала очередного процесса всасывания жидкость, оставшаяся в мертвом пространстве клапанной коробки, расширяется и занимает часть рабочего объема цилиндра, обуславливая уменьшение производительности насоса. Общее понижение действительной производительности по сравнению с теоретической из-за влияния сжимаемости жидкости, а также внутренних перетоков через клапаны внешних утечек, оценивается объемным коэффициентом полезного действия
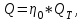(6.32)где: Q - действительная производительность насоса, м3/с
η = 0,8-0,95 - его объемный к.п.д. (насосы большей производительности имеют, как правило, и более высокий к.п.д.).
Как видно из формул теоретическая производительность насоса целиком определяется его конструктивными параметрами и не зависит от давления жидкости. Поэтому поршневые насосы имеют жесткую по расходу напорную характеристику.
Полный к.п.д. насоса определяется следующим образом:
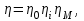(6.33)где: ηi- индикаторный к.п.д., определяемый как отношение площади теоретической и действительной индикаторных диаграмм,
ηМ - механический к.п.д., учитывающий потери энергии на трение в поршневой группе насоса.
Индикаторная диаграмма позволяет, помимо энергетических параметров насоса, оценивать величины сопротивлений всасывающего и нагнетательного клапанов, а также индицировать внутренние неисправности в цилиндре.
Неравномерность подачи возвратно – поступательных насосов.
Использование кривошипно—шатунного механизма в приводе обуславливает изменение скорости движения поршня и подачи жидкости в течение рабочего цикла поршневых и плунжерных насосов.
Пусть на схеме (рис.6.28) точка К отображает крайнее левое положение ползуна в направляющих, а х - линейное перемещение пoлзуна при повороте кривошипа на угол φ.
Рис. 6.28. Схема кривошипно-шатунного механизма поршневого насоса.
По-видимому, линейные перемещения ползуна и поршня одинаковы в любой момент времени и определяются следующим образом:
х=КО-АО, х=(1-cos φ)+l(1-cosβ) (6.34)
где: l – длина шатуна,
β – угол наклона шатуна к оси перемещения ползуна,
r – радиус кривошипа.
Из треугольников ABC и ВОС имеем sinβ=r/l*sin φ
Тогда:
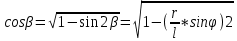(6.35)Разложив последний радикал по формуле бинома Ньютона и отбросив третье и последующие слагаемые как малые величины высших порядков, приближенно получим:
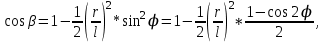(6.36)Линейное перемещение ползуна:
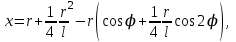(6.37)В кривошипно-шатунных механизмах поршневых насосов обычно принимают r/l =1/5 = 0,2. Если пренебречь вторым слагаемым разложения, которое при максимальной величине = 1 не превышает 0,02, то (6.37) упростится и преобразуется в следующее:
x=r(1-cos φ)=r(1-cos2πωt), (6.38)
где: ω - частота вращения коленчатого вала, об/с,
t - отрезок времени, в течение которого кривошип поворачивав на угол φ относительно оси перемещения ползуна, с.
С учетом (6.38) линейная скорость ползуна (поршня)
Vп=dx/dt=2πωrsin2πωt, (6.39)
а величина линейного ускорения:
ωп=dVn/dt=4π2 ω2 r cos2πωt. (6.40)
Как видно из уравнений (6.39) и (6.40), линейная скорость поршня в пределах цикла изменяется по закону синуса, а ускорение по закону косинуса. Скорость Vn достигает максимальной величины при φ = 90° и φ = 270°, а ускорение - при φ = 0 и φ = 180°, когда поршень находится в крайних положениях.
Если скорость Vn определить с учетом более точного исходного уравнения (6.37) и допустить, что r/l = 0,2, тс ее максимальная величина:
Vмах=4π2 ω2 r(1± r/l), (6.41)
достигается при φ =80°, а максимальное значение ускорения:
ωмах=4π2 ω2 r(1± r/l), (6.42)
где знак плюс относится к крайнему левому положению поршня, а минус - к правому.
В нормально работающем насосе жидкость безотрывно следует за поршнем. При постоянном поперечном сечении поршня текущее значение подачи жидкости будет:
Qt=Fn Vn=2πωrFn sin2πωt, (6.43)
Как видно из рис.6.29, подача одноцилиндрового насоса простого действия в течение его рабочего цикла характеризуется крайней неравномерностью.