ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 39
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
www.dismatem.ru – типовые расчеты по дискретной математике
www.nstu.ucoz.ru – помощь студентам НГТУ

Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Итого
6
+
+
+
+
+
125 р.
З адание 1.
адание 1.
Докажите тождества, используя только определения операций над множествами.
1) 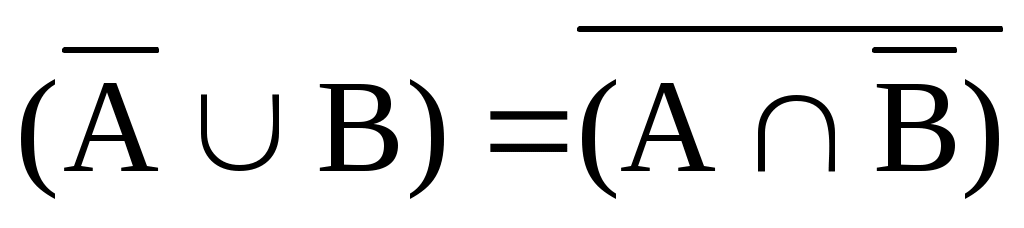
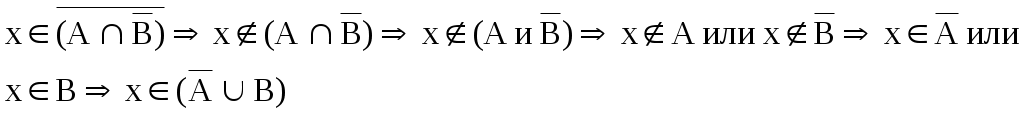
2)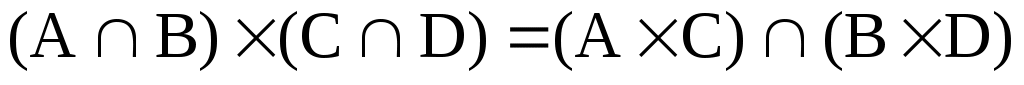
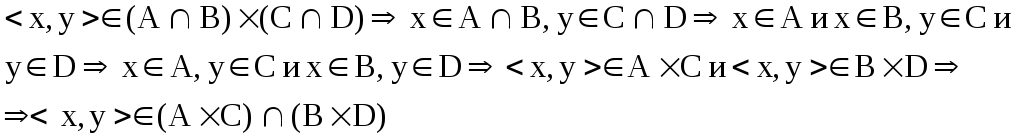


Задание 2.
Докажите утверждение.

Поменяем в множестве Z элементы так, что Z={0,1,-1,2,-2,3,-3,…}, а множество Q представим как последовательность элементов 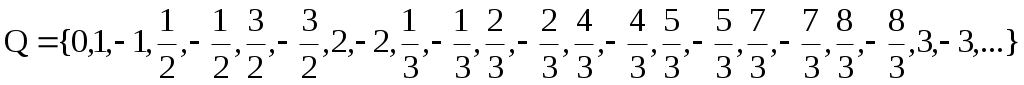 .
.
Получим, что множества Z и Q – счетные, конечные множества. Поэтому можно сказать, что Z
 , и Q
, и Q
| www.dismatem.ru – типовые расчеты по дискретной математике www.nstu.ucoz.ru – помощь студентам НГТУ | |
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Итого |
| 6 | + | + | + | + | + | | | | | | | | | | | | | | 125 р. |
З
 адание 1.
адание 1.Докажите тождества, используя только определения операций над множествами.
1)
2)
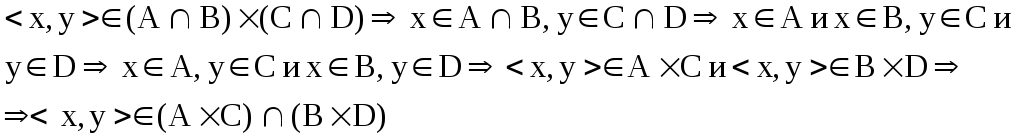


Задание 2.
Докажите утверждение.
Поменяем в множестве Z элементы так, что Z={0,1,-1,2,-2,3,-3,…}, а множество Q представим как последовательность элементов
Получим, что множества Z и Q – счетные, конечные множества. Поэтому можно сказать, что Z
Остается доказать, что
Так как
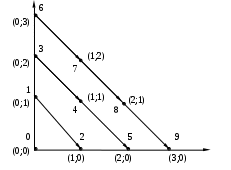
Для доказательства утверждения требуется установить биекцию между множеством натуральных чисел и полученными точками, то есть пронумеровать точки. Сделаем это следующим образом:
0


Задание 3.
Докажите методом математической индукции.
Найдем базис индукции:
n=1
Предположим, что
Докажем, что
(так как n>0)
Значит, так как справедливость утверждения доказана для n+1, то верно и утверждение, то есть


Задание 4.
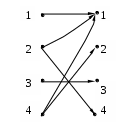
A={a,b,c}, B={1,2,3,4},
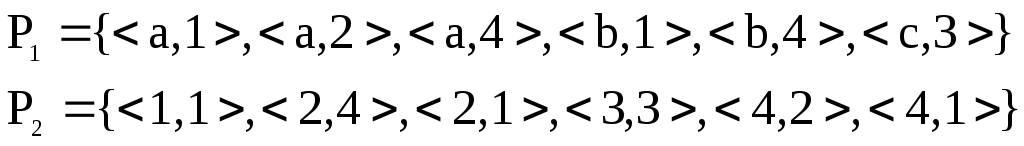
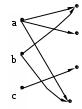
1
2
3
4
[
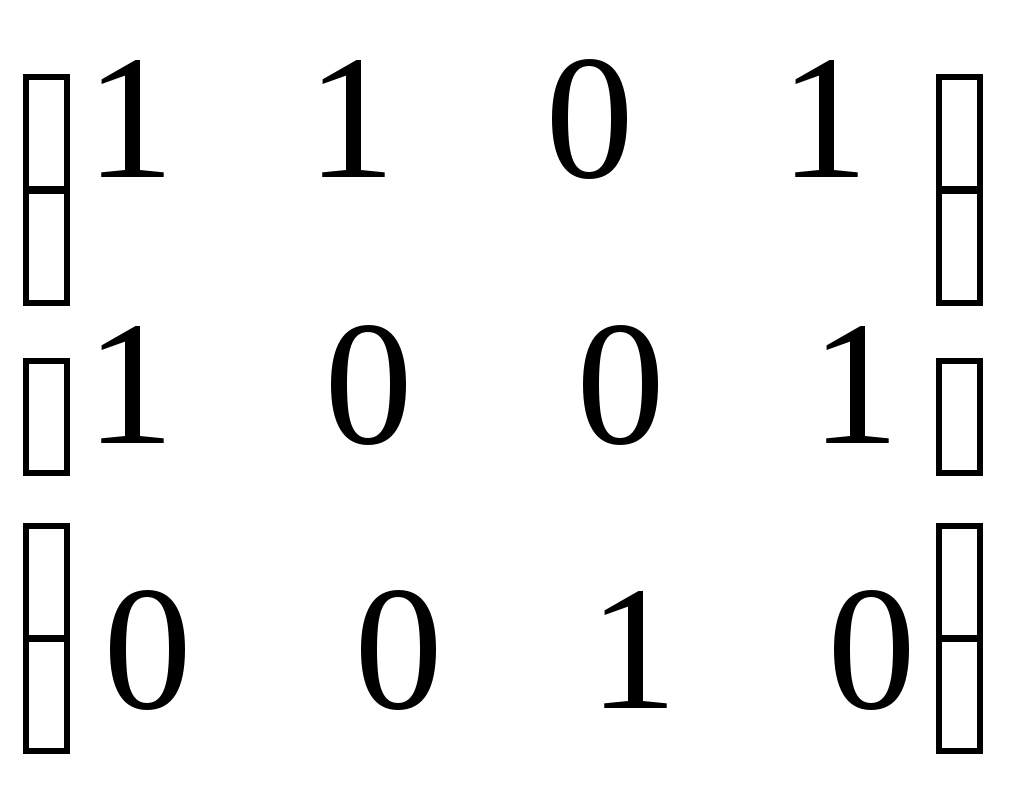
[
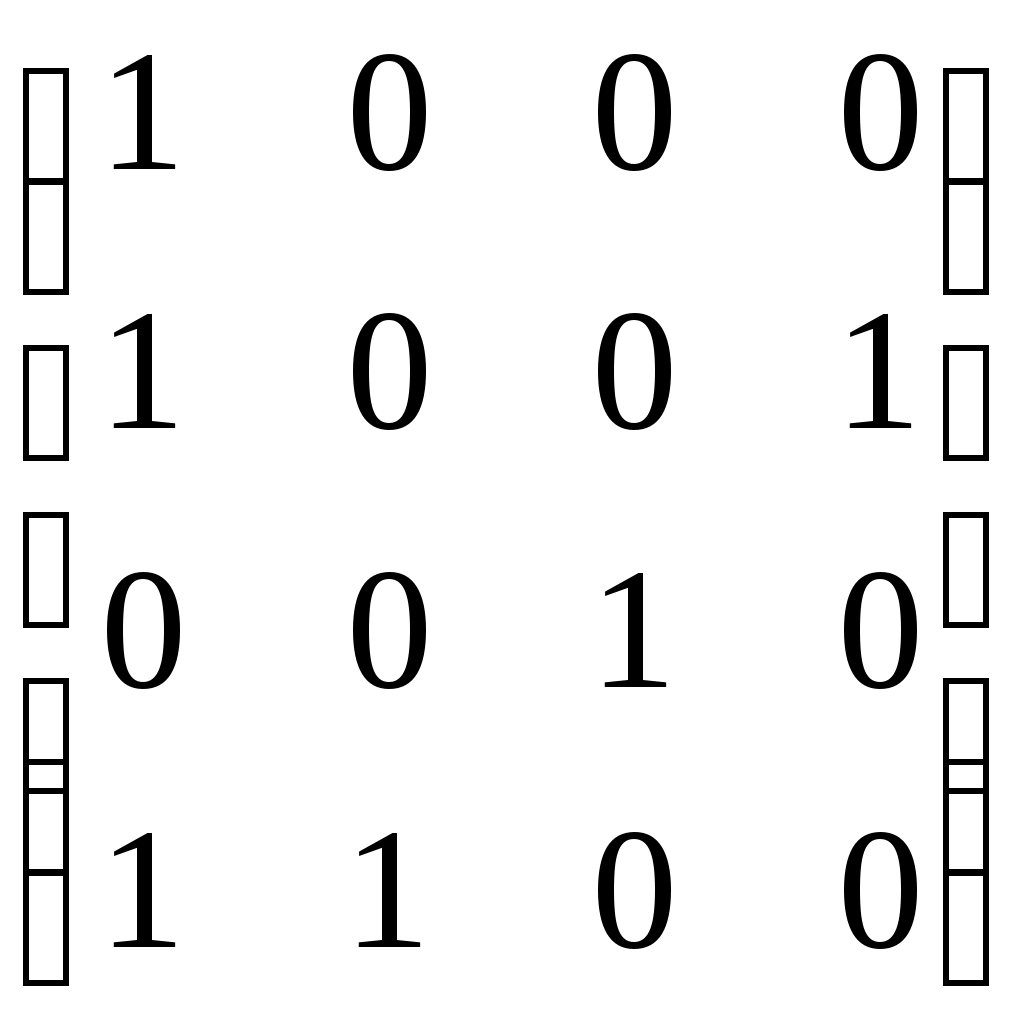
[
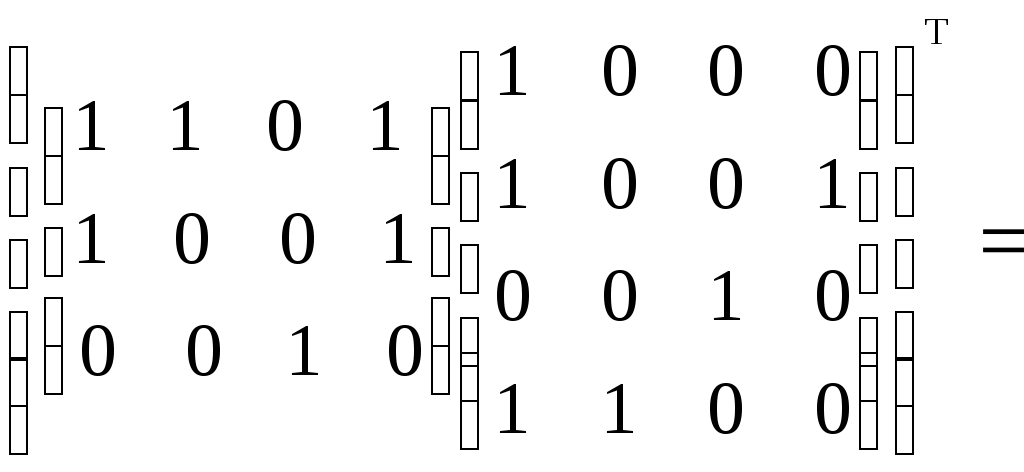
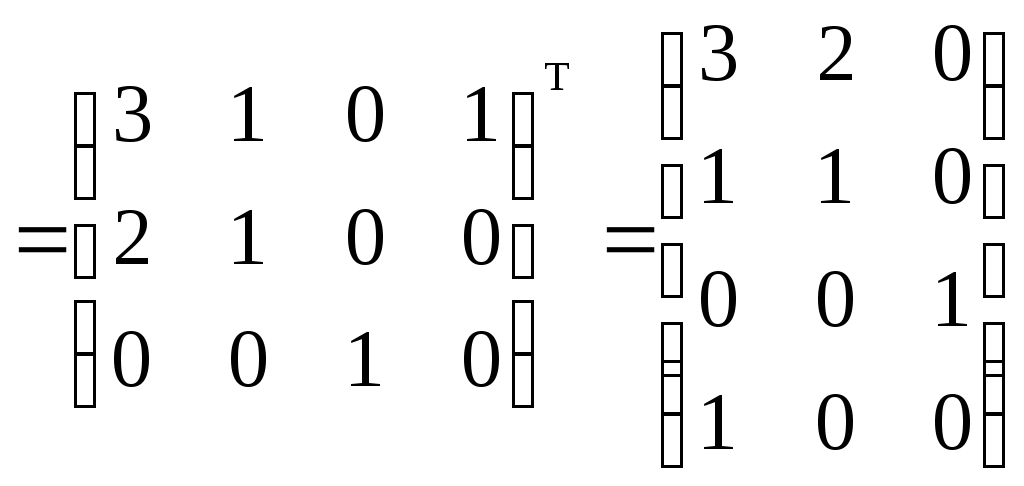
1)
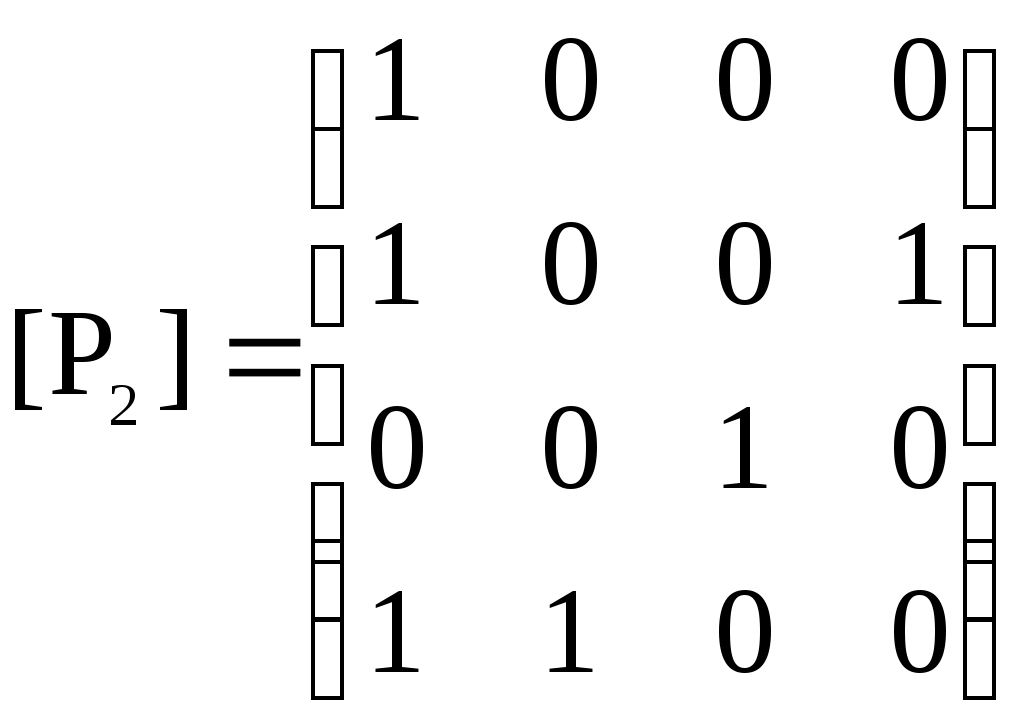 – по диагонали есть нули
– по диагонали есть нули 2)
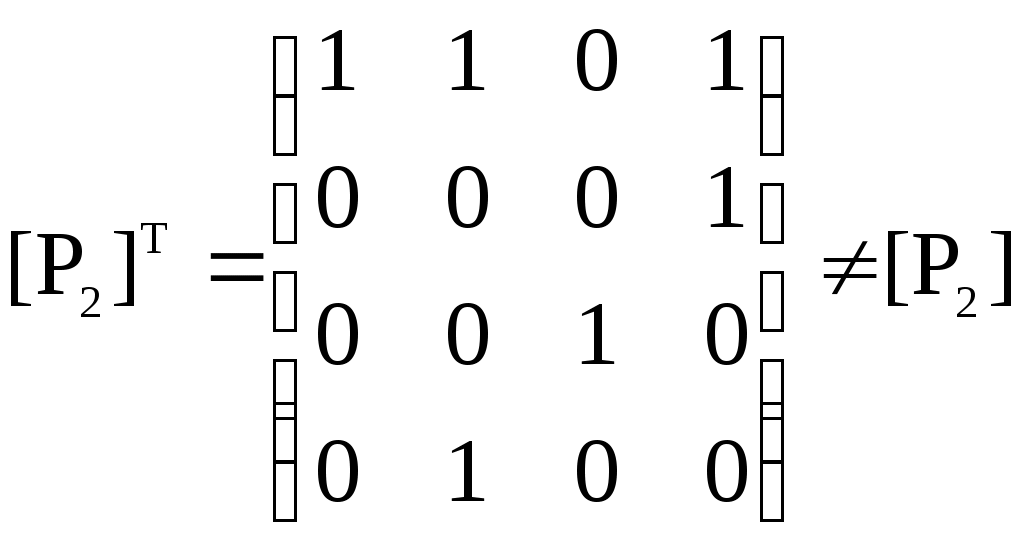
3
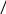 )
)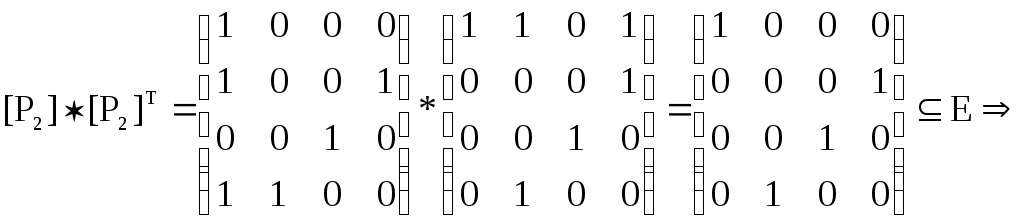
4
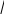 )
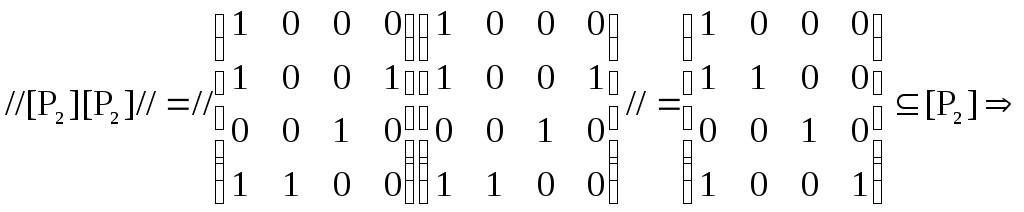
)

З
 адание 5.
адание 5.Найдите область определения, область значений отношения P. Является ли отношение P рефлексивным, симметричным, антисимметричным, транзитивным?
Область определения:
Область значений:
1)
2) Пусть
3) Так как
4) Так как

