Комплексное число имеет вид: 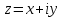;здесь x и y - действительные числа, a i - число нового рода, называемое мнимой единицей. «Мнимые» числа составляют частный вид комплексных чисел (когда x= 0). С другой стороны, и действительные (т. е. положительные и отрицательные) числа являются частным видом комплексных чисел (когда y = 0). Действительное число называется абсциссой комплексного числа 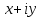; действительное число y - ординатой комплексного числа 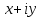. Основное свойство числа i состоит в том, что произведение ii равно -1, т. е.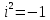Суммой z₁+z₂ двух комплексных чисел z₁=(x₁,y₁) и z₂=(x₂,y₂) называют комплексное число 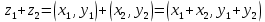(1.1) а произведением z₁z₂ этих комплексных чисел — комплексное число 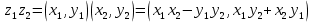. (1.2) Элемент O= (0,0) поля комплексных чисел является нейтральным относительно операции сложения, и его называют нулевым элементом этого поля. На плоскости xOy он совпадает с началом координат. Элемент (1,0) является нейтральным относительно операции умножения, и его называют единицей поля комплексных чисел. Особую роль играет комплексное число (0, 1), которое обозначают i и называют мнимой единицей. Согласно (1.2), имеем 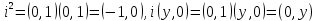. (1.3) Каждую упорядоченную пару (x, 0) ϵ R сопоставим с числом x ϵ R. Возникает взаимно однозначное соответствие между множеством R действительных чисел и множеством упорядоченных пар вида (x, 0), при котором сумме и произведению действительных чисел отвечают сумма и произведение соответствующих им упорядоченных пар. Поэтому каждую упорядоченную пару вида (x, 0) отождествляют с числом x. В этом случае каждую упорядоченную пару можно представить в виде 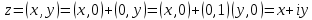. (1.4) Выражение

---

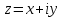
представляет собой алгебраическую (или декартову) форму записи (представления) комплексного числа. В этой записи x и y — действительные числа, причем называют действительной частью комплексного числа z и обозначают Re z , а y называют мнимой частью комплексного числа и обозначают Im z . Таким образом, в записи (1.4)
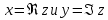. (1.5)
Комплексное число равно нулю (z = 0) в том и только в том случае, когда его действительная и мнимая части одновременно равны нулю. Элементы поля C комплексных чисел можно отождествить с точками плоскости, рассматривая действительную x и мнимую y части комплексного числа как координаты точки М (x, y) в некоторой фиксированной прямоугольной системе координат Oxy(рис. 1.1).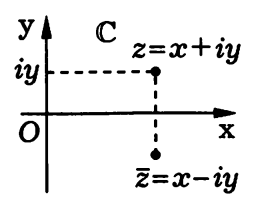

В этом случае плоскость Oxy называют комплексной плоскостью (или плоскостью комплексных чисел) и обозначают либо (как и это поле) символом C, либо заключенным в круглые скобки обозначением комплексного числа: (z), (ω). Произвольному действительному числу x соответствует точка (x ,0) комплексной плоскости, лежащая на оси абсцисс, которую применительно к плоскости C называют действительной (или вещественной) осью. Чисто мнимому числу iy соответствует точка (0; y) плоскости C, расположенная на оси ординат, называемой в данном случае мнимой осью (но по традиции обозначаемой y, а не iy!).

Комплексному числу соответствует точка М (x, y) комплексной плоскости. При этом абсцисса точки совпадает с действительной частью комплексного числа, а ордината точки — с его мнимой частью. Интерпретация комплексных чисел как точек плоскости позволяет говорить о геометрической форме представления комплексного числа. Далее точку М(x , y) плоскости C с координатами x и y будем обозначать так же, как и соответствующее ей комплексное число .

Операции сложения (1.1) и умножения (1.2) обладают свойствами коммутативности и ассоциативности

---

, а умножение обладает свойством дистрибутивности относительно сложения.

Два комплексных числа, записанных в алгебраической форме, равны в том и только в том случае, когда равны соответственно их действительные и мнимые части. Применительно к этой форме записи правила (1.1) и (1.2) дают
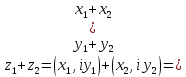(1.6)

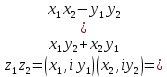(1.7)
и приводят практически к простому условию, что все действия над комплексными числами аналогичны действиям над многочленами, но с учетом свойств мнимой единицы
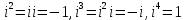и т.д. (1.8)
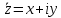Числа и называют комплексно сопряженными. На плоскости C им соответствуют точки, расположенные симметрично относительно действительной оси (см. рис. 1.1).

Сумма и произведение сопряженных комплексных чисел являются действительными числами, а разность — чисто мнимым числом:
.



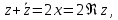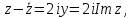
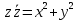(1.9)
Для сложения и умножения существуют обратные операции: соответственно вычитание и деление (кроме деления на нуль), которые в алгебраической форме можно записать следующим образом:
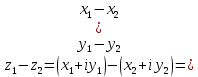(1.10)
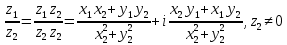. (1.11)
Пример 1. Найти значение выражения 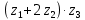, если .

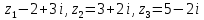Решение: ,



.

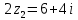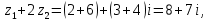
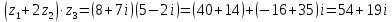Ответ: .

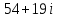Пример 2. Найти значение выражения 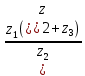, где , .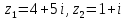

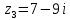Решение:

---

,

,



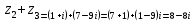
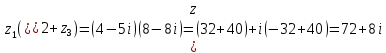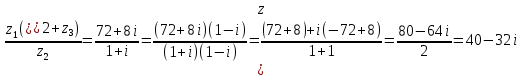
Ответ:

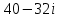
Пример 3. Вычислите:

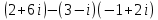
Решение:

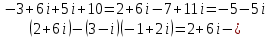
Ответ:

.

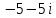
Пример 4. Докажите, что 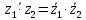для любых комплексных чисел 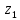и .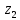

Решение: Представим данные числа в алгебраической форме:

, .

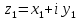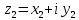Тогда



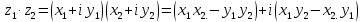
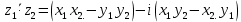
Далее,



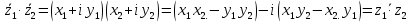
что и требовалось доказать.

---

Смотрите также файлы

• Примерные задания к контрольной работе Задание 1.docx

• Отчет по производственной практике пп 04. 01 Пм. 0.docx

• 1. Проектирование холодного водоснабжения здания 5 1 Выбор системы и схемы внутреннего водопровода 5.docx

• ысамерзімді жоспар 1 саба.docx

• Технологическая (проектнотехнологическая) практика).docx