Файл: Контрольная работа по теме Площади поверхностей тел вращения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 89
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа по теме «Площади поверхностей тел вращения». 1 вариант.
1.Цилиндр.
1.1.Радиус основания цилиндра равен 5, высота равна 8. Найдите площадь боковой поверхности цилиндра, деленную на π.
1.2. Длина окружности основания цилиндра равна 16. Площадь боковой поверхности равна 8. Найдите высоту цилиндра.
1.3. Площадь боковой поверхности цилиндра равна 80π, а диаметр основания — 5. Найдите высоту цилиндра.
1.4. Длина окружности основания цилиндра равна 9, высота равна 7. Найдите площадь боковой поверхности цилиндра.
1.5. Площадь осевого сечения цилиндра равна 36. Найдите площадь боковой поверхности цилиндра, деленную на π.
2.Конус.
2.1. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 40 раз?
2.2. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 2,5 раза, а образующая останется прежней?
2.3. Площадь полной поверхности конуса равна 600. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
2.4. Высота конуса равна 24, а диаметр основания – 14. Найдите образующую конуса.
2.5. Высота конуса равна 39, а длина образующей — 89. Найдите диаметр основания конуса.
2.6. Длина окружности основания конуса равна 9, образующая равна 6. Найдите площадь боковой поверхности конуса.
2.7. Высота конуса равна 20, образующая равна 29. Найдите площадь его полной поверхности, деленную на π.
2.8. Площадь полной поверхности конуса равна 296. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
2.9. Площадь основания конуса равна 48π, высота — 18. Найдите площадь осевого сечения конуса.
2.10. Площадь основания конуса равна 72. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 6 и 12, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
3.Шар.
3.1. Площадь большого круга шара равна 22. Найдите площадь поверхности шара.
3.2. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 50 раз?
3.3. Даны два шара. Диаметр первого шара в 12 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
4.Комбинированные тела.
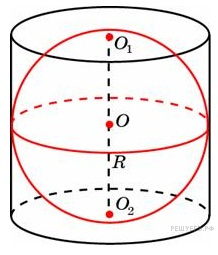
4.1. Около шара описан цилиндр, площадь поверхности которого равна 78. Найдите площадь поверхности шара.
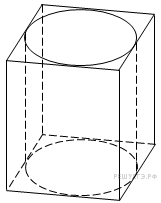
4.2. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 4. Площадь боковой поверхности призмы равна 192. Найдите высоту цилиндра.
4.3. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
4.4.
Задания № 1.5, 2.3,2.8,2.9, 2.10, 3.2, 3.3 – по 2 балла.
Задания раздела 4 – по 3 балла.
Все остальные задания – по 1 баллу.
Оценивание работы: на «3» - 5- 9 баллов(при обязательном условии решения заданий из разделов № 1,2,3).
На «4» - от 10 до 15 баллов(при обязательном условии решения заданий из каждого раздела).
На «5» - от 16 баллов (при обязательном условии решения заданий из каждого раздела).
Контрольная работа по теме «Площади поверхностей тел вращения». 2 вариант.
1.Цилиндр.
1.1.Радиус основания цилиндра равен 9, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на π.
1.2. Длина окружности основания цилиндра равна 15. Площадь боковой поверхности равна 45. Найдите высоту цилиндра.
1.3. Площадь боковой поверхности цилиндра равна
70π, а диаметр основания — 7. Найдите высоту цилиндра.
1.4. Длина окружности основания цилиндра равна 11, высота равна 5. Найдите площадь боковой поверхности цилиндра.
1.5. Площадь осевого сечения цилиндра равна 72. Найдите площадь боковой поверхности цилиндра, деленную на π.
2.Конус
2.1. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 20 раз?
2.2. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 4,5 раза, а образующая останется прежней?
2.3. Площадь полной поверхности конуса равна 400. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
2.4. Высота конуса равна 21, а диаметр основания – 40. Найдите образующую конуса.
2.5. Высота конуса равна 77, а длина образующей — 85. Найдите диаметр основания конуса.
2.6. Длина окружности основания конуса равна 6, образующая равна 4. Найдите площадь боковой поверхности конуса.
2.7. Высота конуса равна 12, образующая равна 13. Найдите площадь его полной поверхности, деленную на π.
2.8. Площадь полной поверхности конуса равна 444. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
2.9. Площадь основания конуса равна 32π, высота — 12. Найдите площадь осевого сечения конуса.
2.10. Площадь основания конуса равна 144. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 12 и 24, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
3.Шар.
3.1. Площадь большого круга шара равна 18. Найдите площадь поверхности шара.
3.2. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 40 раз?
3.3. Даны два шара. Диаметр первого шара в 10 раз больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
4.Комбинированные тела.
4.1. Около шара описан цилиндр, площадь поверхности которого равна 117. Найдите площадь поверхности шара.


4.2. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.
4.3. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна
4.4.
Задания № 1.5, 2.3,2.8,2.9, 2.10, 3.2, 3.3 – по 2 балла.
Задания раздела 4 – по 3 балла.
Все остальные задания – по 1 баллу.
Оценивание работы: на «3» - 5- 9 баллов(при обязательном условии решения заданий из разделов № 1,2,3).
На «4» - от 10 до 15 баллов(при обязательном условии решения заданий из каждого раздела).
На «5» - от 16 баллов (при обязательном условии решения заданий из каждого раздела).