---

5. Контрольные вопросы.

1. Сформулируйте цель лабораторной работы и поясните, как достигается поставленная цель?

2. Назовите основные узлы экспериментальной установки и укажите их назначение.

3. Как Вы понимаете такие состояния, как насыщенный и ненасыщенный влажный воздух?

4. Как Вы относитесь к термину «пересыщенный» влажный воздух?

5. Как формулируется и записывается закон парциальных давлений для влажного воздуха?

6. Что называется абсолютной, относительной влажностью и влагосодержанием влажного воздуха?

7. Как выражается и из чего складывается теплосодержание (энтальпия) влажного воздуха?

8. Почему с увеличением температуры влажного воздуха его относительная влажность уменьшается?

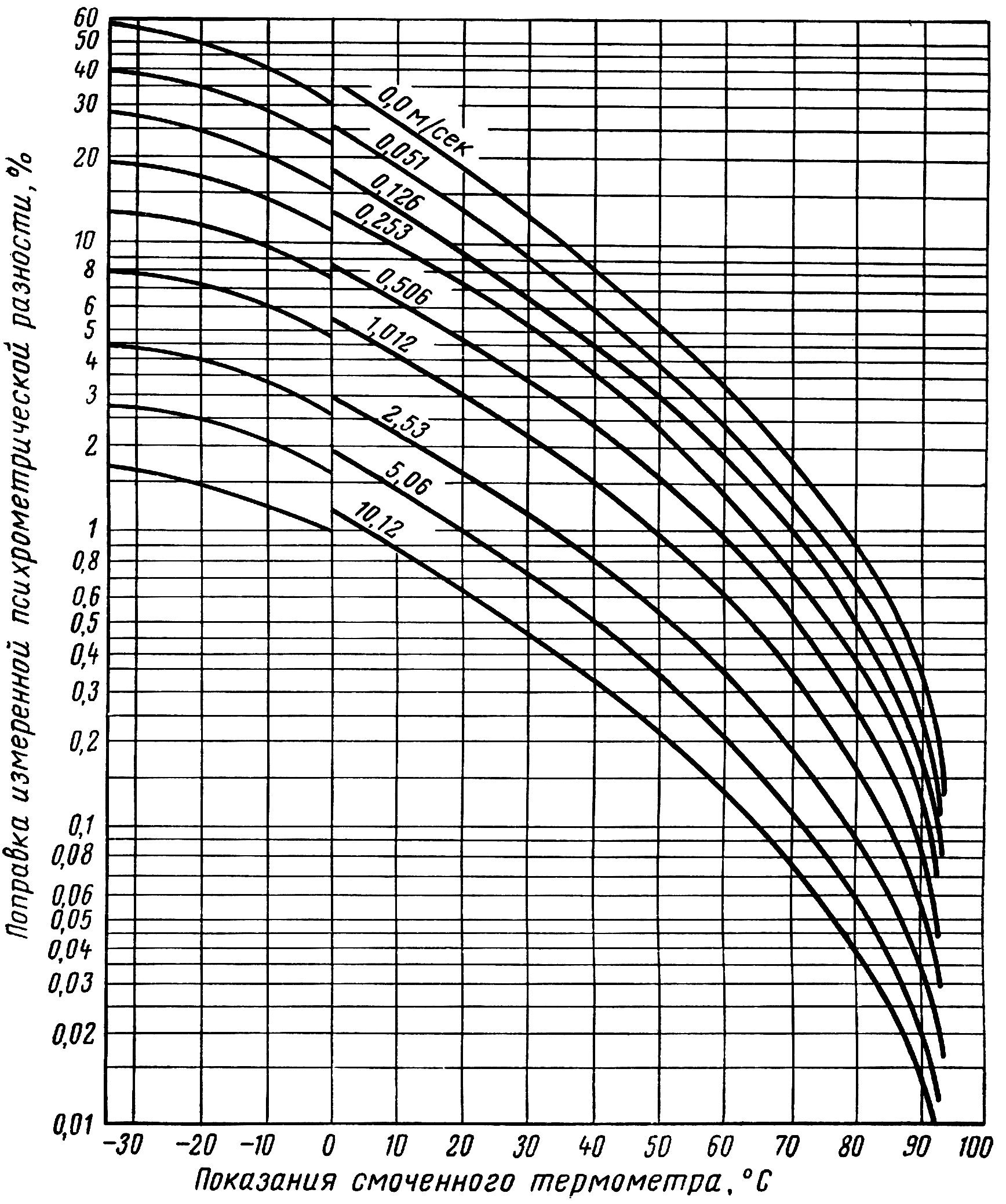
9. Чем Вы можете объяснить влияние скорости воздуха на отклонение показания смоченного термометра от истинного значения температуры мокрого термометра?

10. Как устроена диаграмма I-d влажного воздуха и, каким образом определяются параметры влажного воздуха с помощью диаграммы по показаниям сухого и мокрого термометров?

11. Покажите на диаграмме и поясните процессы «сухого» нагрева и охлаждения влажного воздуха.

12. Покажите на диаграмме и поясните процесс адиабатного насыщения влажного воздуха.

13. Дайте определение понятию точки росы. Как определяется температура точки росы на диаграмме?

14. Какова связь между относительной влажностью воздуха и его влагосодержанием?

15. Дайте вывод аналитической формулы для расчета абсолютной влажности воздуха.

16. Дайте вывод аналитической формулы для расчета влагосодержания воздуха.

17. Дайте вывод аналитической формулы для расчета теплосодержания (энтальпии) воздуха.
П 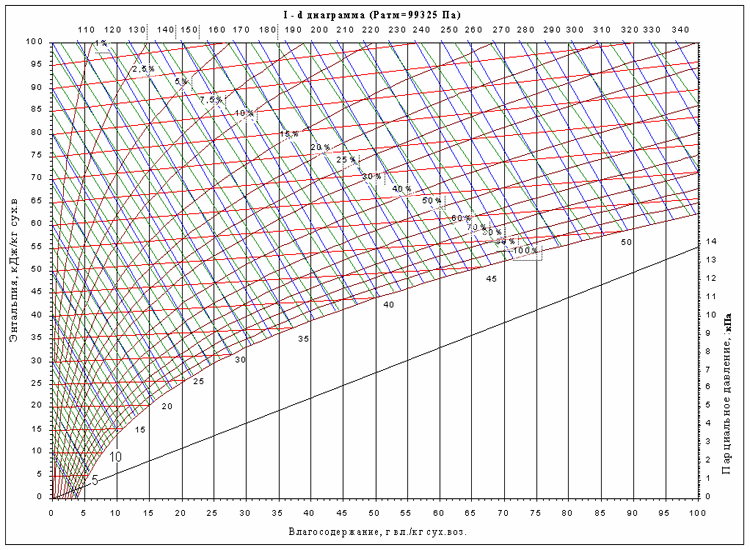риложение 1

Приложение 2

Работа 3. ИССЛЕДОВАНИЕ ПРОЦЕССА ИСТЕЧЕНИЯ ВОЗДУХА
ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО
1. Цель работы.

И сследование зависимости массового расхода воздуха через суживающееся сопло от отношения давления за соплом к давлению перед соплом.

---

2. Основные положения. Канал, в котором с уменьшением давления скорость газового потока возрастает, называется соплом; канал, в котором скорость газа уменьшается, а давление возрастает, называется диффузором. Поскольку назначением сопла является преобразование потенциальной энергии рабочего тела в кинетическую, то для анализа происходящего в нем процесса, начальная скорость потока является несущественной, и ее можно принять W₁ = 0. Тогда уравнение первого закона термодинамики при адиабатном истечении рабочего тела через сопло принимает вид:

,

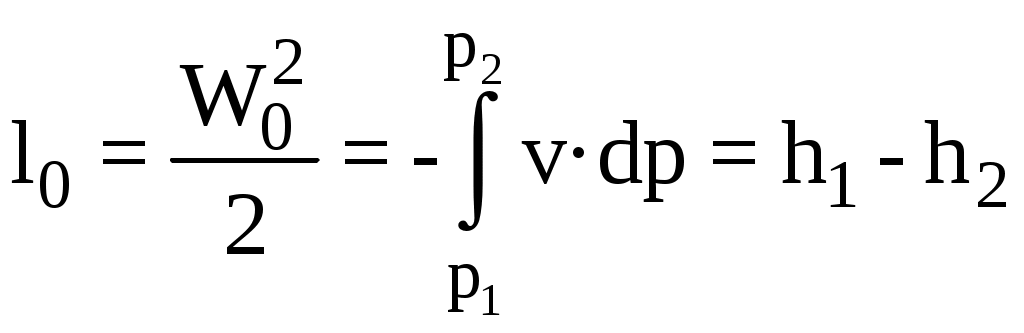где W₀ —теоретическая скорость потока в выходном сечении сопла; Р₁ — начальное давление рабочего тела; Р₂ — давление среды, в которую происходит истечение.

Разность энтальпий (h₁ – h₂) при истечении через сопла также называется располагаемым теплоперепадом и обозначается через h₀. Она соответствует тому максимуму кинетической энергии, который может быть получен лишь в идеальных условиях истечения, а фактически из-за неизбежных потерь, связанных с необратимостью процесса, никогда не достигается.

Исходя из равенства W₀²/2 = h₀, теоретическую скорость истечения (W₀, м/с) рабочего тела через сопло в рассматриваемом случае можно определить по формуле:

.

Здесь h₀ выражено в кДж/кг. Это соотношение справедливо для любого рабочего тела.

Р 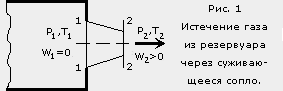ассмотрим адиабатное истечение газа через суживающееся сопло из резервуара (рис.1) достаточно большого объема, в котором изменением давления можно пренебречь (Р₁ ≈ const).

В резервуаре газ имеет параметры Р₁, T₁, v₁ (ρ₁), а на выходе из сопла Р₂, Т₂, v₂ (ρ₁), W₂. Давление среды, в которую происходит истечение газа, обозначим Р₀. Основной характеристикой процесса истечения является отношение конечного давления к начальному, т. е. величина β= Р₀/Р₁.

В зависимости от отношения давлений можно выделить три характерных режима истечения газа: при β>β

---

_кр − докритический, при β = β_кр − критический и при β<β_кр− сверхкритический режимы.

Значение β, при котором расход газа достигает максимума, называется критическим β_кр, и находится по формуле:

.

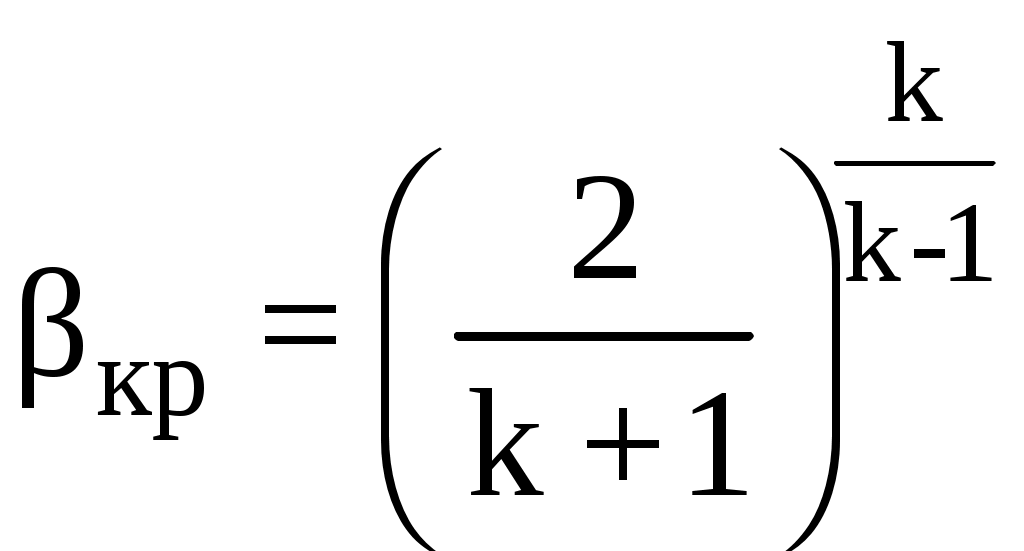Как и показатель адиабаты, величина β_кр является физической константой газа, т. е. одной из характеристик его физических свойств.

П 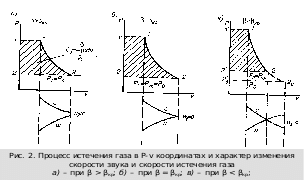ри докритическом режиме истечения (β>β_кр) в сопле происходит полное расширение газа с понижением давления от Р₁ до Р₀, на срезе сопла Р₂ = Р₀, скорость на выходе меньше скорости звука (рис. 2,а), располагаемая работа, соответствующая площади 1'-1-2-2'-1', полностью расходуется на увеличение кинетической энергии газа. При критическом режиме (β = β_кр) также происходит полное расширение газа в пределах сопла, на срезе сопла Р₂ = Р_кр = Р₁·β_кр = Р₀, скорость на выходе равна критической скорости – скорости звука (рис. 2,б), располагаемая работа полностью расходуется на увеличение кинетической энергии газа. При сверхкритическом режиме (β<β_кр) в пределах сопла происходит неполное расширение газа, давление понижается только до критического, на срезе сопла Р₂=Р_кр=Ρ₁·β_кр>Ρ₀, скорость на выходе равна критической скорости – местной скорости звука (рис.2, в).
Дальнейшее расширение газа и понижение его давления до Р₀ осуществляется за пределами сопла. На увеличение кинетической энергии расходуется только часть располагаемой работы, соответствующая площади 1'-1-2-2'-1', другая ее часть, соответствующая площади 2'-2-2₀ -2₀'-2', в суживающемся сопле остается не реализуемой.

Скорость газа на выходе из суживающегося сопла определяется по формулам:

для первого случая, когда β>β_кр Р₂ = Р₀:

,

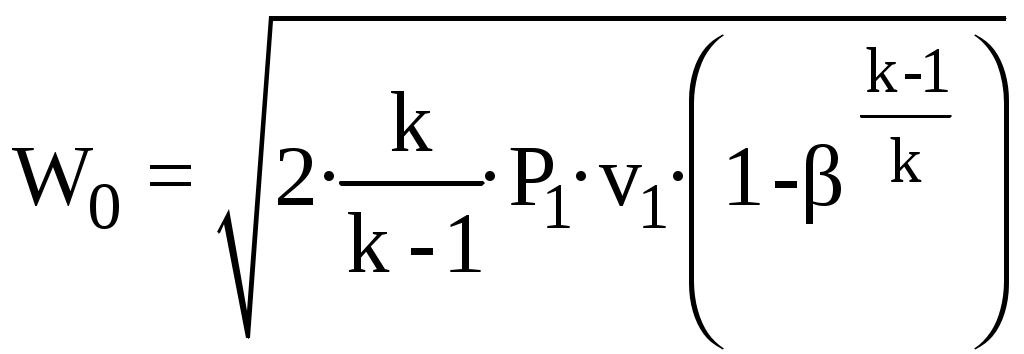для второго и в третьего случаев, когда β = β_кр, а Р₂ = Р_кр = Р₁·β_кр = Р₀ и β<β_кр, а Р₂=Р_кр=Ρ₁·β_кр>Ρ₀

,

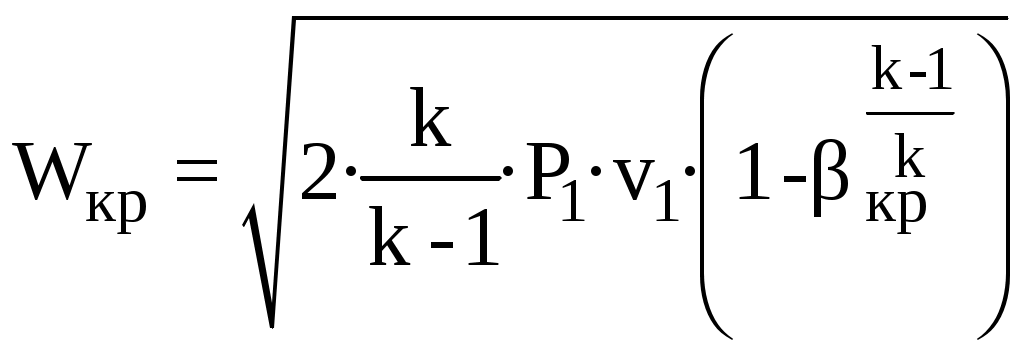или, подставив значение β_кр из формулы (3), получим:

---

,

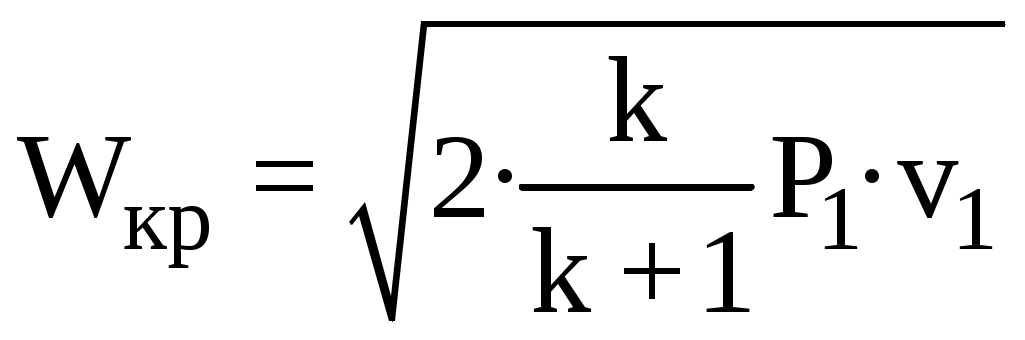тогда при условиях адиабатного истечения

.

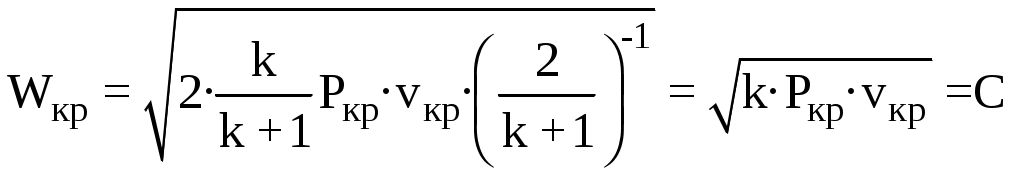Полученная формула показывает, что критическая скорость истечения газа из сопла равна скорости распространения звуковой волны в этом газе при его параметрах Р_кр и v_кр, т е местной скорости звука С в выходном сечении сопла.

В этом содержится физическое объяснение тому, что при снижении внешнего давления Р₀ ниже Р_кр скорость истечения не изменяется, а остается равной W_кр.

Действительно, если Р₀>Р_кр, то W₀кр или W₀0 передается вдоль сопла в направлении, обратном движению потока, со скоростью (C − W₀) > 0. При этом происходит перераспределение давления и скоростей по всей длине сопла· в каждом промежуточном сечении устанавливается новая скорость, соответствующая большему расходу газа. Если же Р₀ снизится до Р_кр, то дальнейшее понижение его уже не сможет распространяться вдоль сопла, поскольку скорость его распространения навстречу потоку снизится до нуля (C − W_кр) = 0. Поэтому в промежуточных сечениях сопла расход газа не изменится, не изменится он и в выходном сечении, т е скорость истечения останется постоянной и равной W_кр.

Зависимость скорости и расхода газа на выходе из суживающегося сопла от отношения давлений β = Р₀/Р₁ показана на рис. 3. Экспериментально эта зависимость была получена А.Сен-Венаном в 1839 году.





В отличие от теоретического изоэнтропийного действительный процесс истечения реального газа происходит при трении частиц газа между собой и о стенки канала. При этом работа, затрачиваемая на преодоление сил трения, преобразуется в теплоту, в результате чего температура и энтальпия газа в выходном сечении канала возрастают.

Истечение газа с трением становится необратимым процессом и сопровождается увеличением энтропии.

На рис. 4 в sh - координатах представлены процессы расширения газа 1-2 при истечении без трения и 1-2д при истечении с трением.





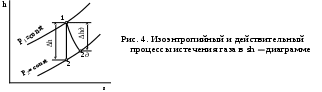
При одинаковом перепаде давлений Р₁ − Р₂ действительный теплоперепад Δh_д = h₁-h_2д меньше располагаемого Δh = h₁ − h₂. В результате этого действительная скорость истечения газа оказывается меньше теоретической.

Отношение разности располагаемого и действительного теплоперепадов (потери теплоперепада) к располагаемому теплоперепаду называется коэффициентом потери энергии



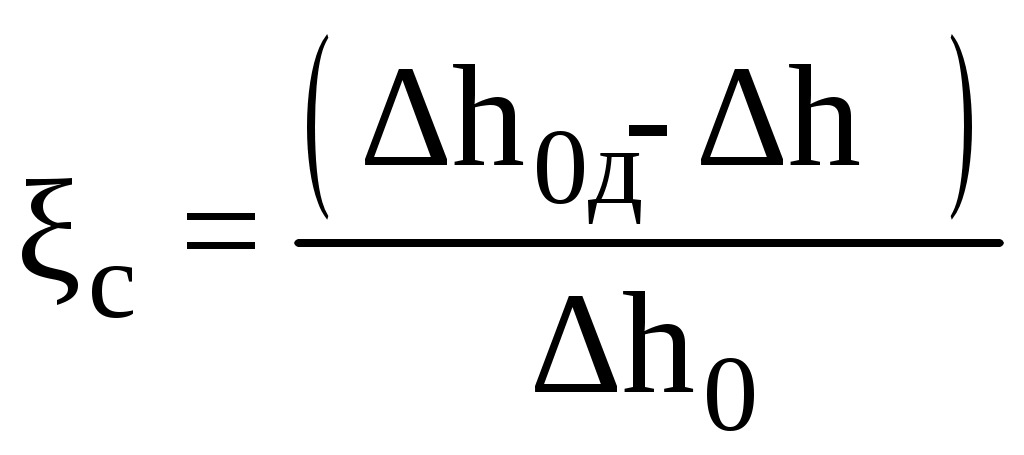
Коэффициентом потери скорости называется отношение действительной скорости истечения к теоретической

.

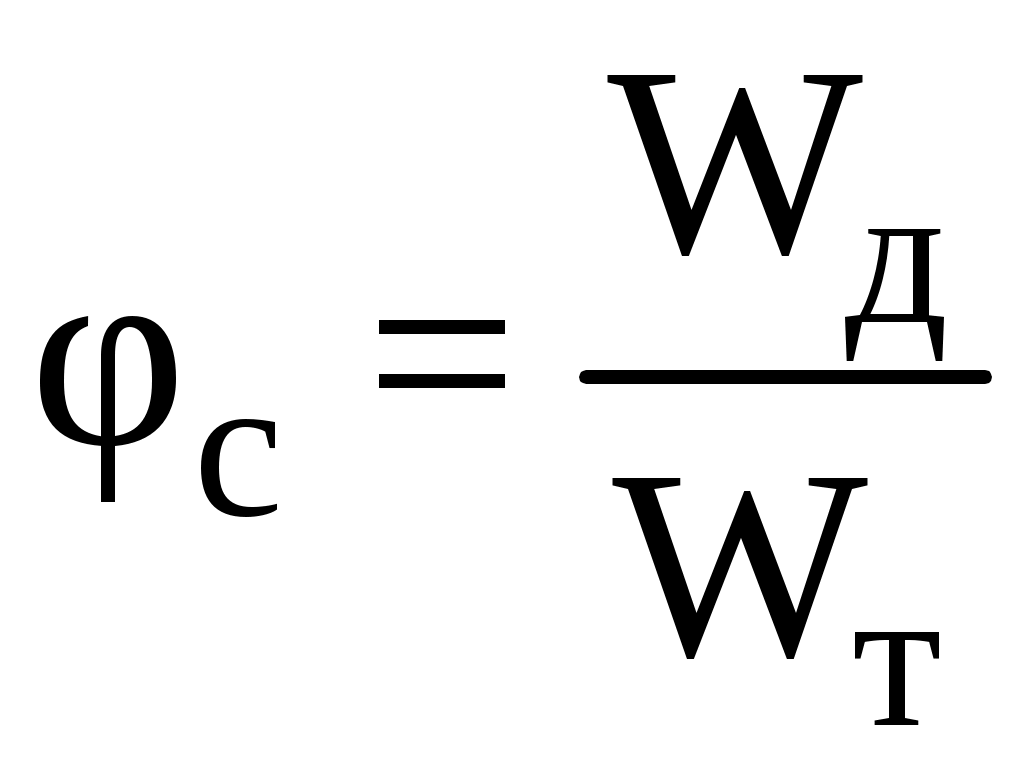Коэффициент потери скорости, учитывающий уменьшение действительной скорости по сравнению с теоретической, в современных соплах равен 0,95 - 0,98 .

Отношение действительного теплоперепада Δhд к теоретическому Δh, или действительной кинетической энергии W_д²/2 к теоретической W²/2 называется коэффициентом полезного действия канала

.

.

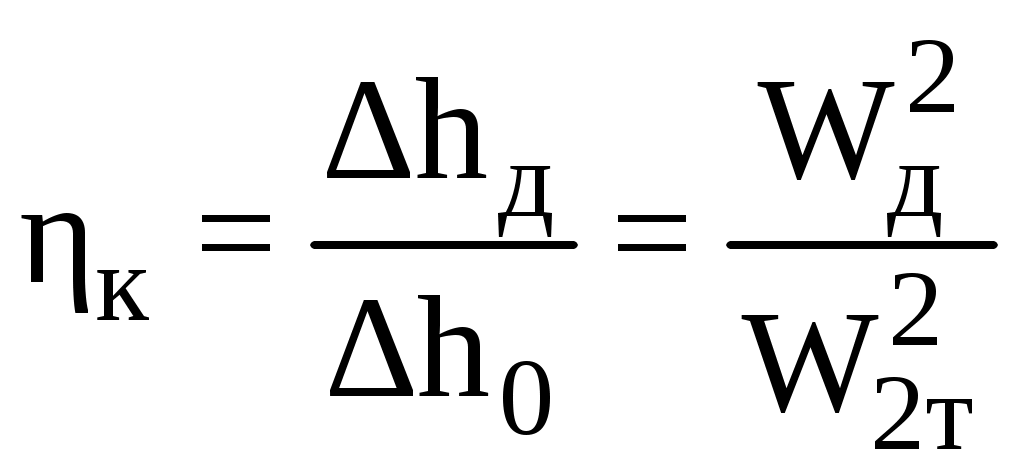3. Схема и описание установки.

Воздух от ресивера поршневого компрессора



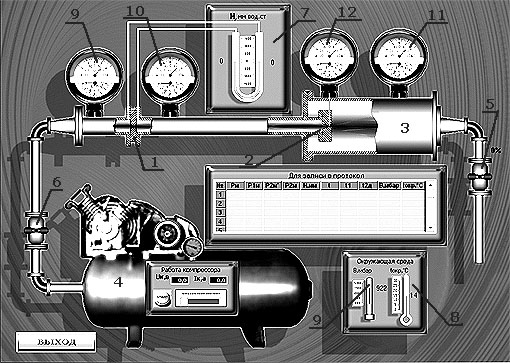
(на схеме не показан) (рис. 5) по трубопроводу поступает через измерительную диафрагму 1 к суживающемуся соплу 2. В камере 3 за соплом, куда происходит истечение, можно устанавливать различные давления выше барометрического путем изменения проходного сечения для воздуха с помощью вентиля 5. А затем воздух направляется в атмосферу. Сопло выполнено с плавным сужением. Диаметр выходного сечения сопла 2,15 мм. Суживающийся участок сопла заканчивается коротким цилиндрическим участком с отверстием для отбора и регистрации давления Р_2м′ и температуры t_2д в выходном сечении сопла (прибор 12).. Измерительная диафрагма 1 представляет собой тонкий диск с круглым отверстием по центру и вместе с дифманометром 7 служит для измерения расхода воздуха.

Температура и давление воздуха в окружающей среде измеряются соответственно термометром 8 и чашечным ртутным барометром 6.

Т емпература и давление воздуха перед измерительной диафрагмой замеряются с помощью комбинированного прибора 9 , а перед соплом − прибором 10. Давление за соплом измеряется манометрической частью комбинированного прибора 11. Все показания приборов заносятся в протокол наблюдений (таблица 1).
Протокол наблюдений

Таблица 1.

№ п/п	Измеряемая величина	Обозна- чение	Номера опытов
			1	2	3	4	5	6	7	8	9	10	11	12
1	Показание манометра перед диафрагмой, ати	Рм
2	Показание манометра перед соплом, ати	Р1м
3	Показание манометра в выходном сечении сопла, ати	Р2м'
4	Показание манометра за соплом, ати	Р2м
5	Показания дифманометра, мм вод.ст.	H
6	Температура перед диафрагмой, °С	t
7	Температура перед соплом, °С	t1
8	Температура в выходном сечении сопла, °С	t2д
9	Показания барометра, мбар	B
10	Температура окружащей среды, °С	tокр

4. Расчетные формулы и расчеты.

1. Атмосферное давление (Р_атм, бар) находится с учетом температурного расширения столбика ртути барометра по формуле:

.

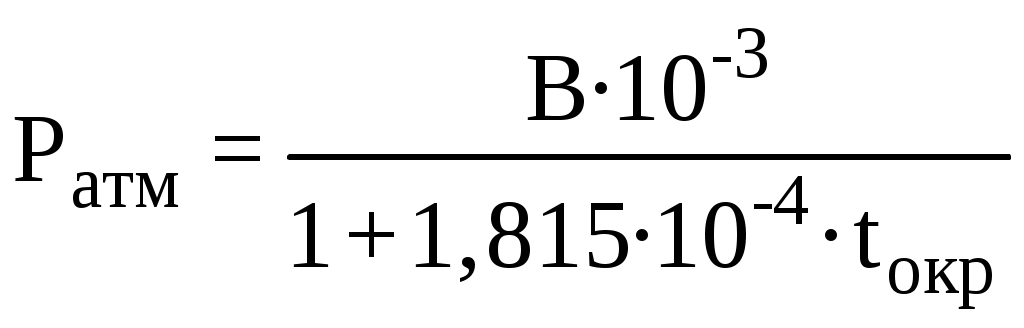2. Перевод показаний образцовых манометров Р_м, Р_1м, Р_2м' и Р_2м в абсолютные значения (р, бар) давлений по формулам:

-давление перед диафрагмой ;

-давление перед соплом ;

-давление в устье сопла ;

-давление за соплом ;

где 1,019 − переводной коэффициент показаний манометров из ат в бар.

3. Перепад давления (ΔР, Па) воздуха на диафрагме:

,

где g = 9,81– ускорение свободного падения, м/сек²; Н – показание дифманометра, мм вод.ст.

4. Плотность воздуха (ρ, кг/м³) по состоянию перед диафрагмой:

,

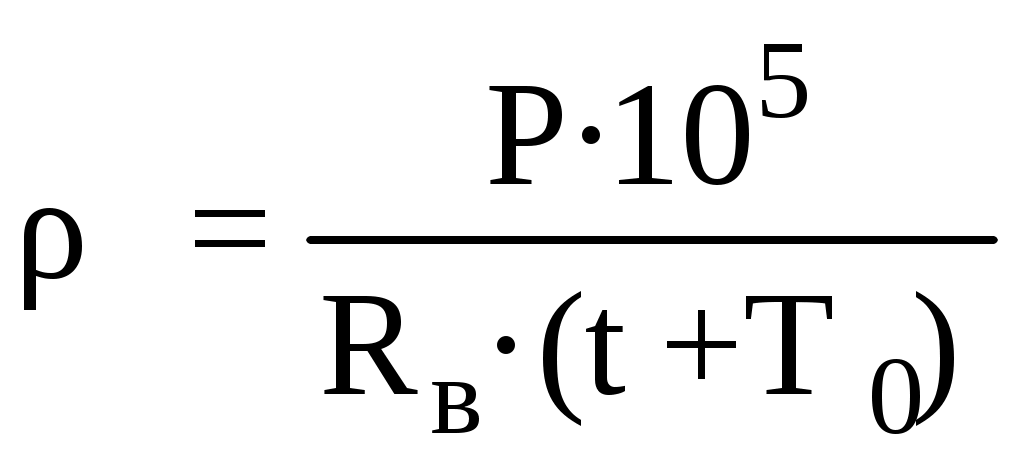где Rв – характеристическая газовая постоянная воздуха, равная 287 Дж/кг·К, t – температура воздуха перед диафрагмой, °С, Т₀ = 273,15 – нулевое значение температуры в градусах К.

5. Действительный расход воздуха (G_д, кг/сек) через диафрагму (следовательно, через сопло):

,

где k_v = 2,745 - коэффициент расхода воздуха через диафрагму.

6. Теоретическая скорость истечения (W₂, м/сек) в выходном сечении сопла:

,

где Δh₀ – теоретический адиабатный теплоперепад, кДж/кг.

7. Значения энтальпий воздуха (h₁ и h₂,кДж/кг) в сечениях на входе и на выходе из сопла определяются по общему уравнению:

,

где с_р – теплоемкость воздуха при постоянном давлении, которая может быть принята не зависящей от температуры и равной 1,006 кДж/(кг·°С); t_j – температура в рассматриваемом сечении, °С; j – индекс рассматриваемого сечения.

8. Теоретическое значение температуры (Т₂, К) в выходном сечении сопла находится из условия адиабатного процесса истечения по формуле:

, а t₂ = T₂ − 273,15 °C ,

где β_расч – расчетное значение отношения давлений. Величину β_расч принимают по данным таблицы результатов расчета (таблица 2) для конкретного опыта, когда режим истечения до критический β_расч = β_табл; для всех остальных опытов, когда режим истечения критический или за критический величина β_расч принимается равной β_кр (независимо от данных таблицы 2) и находится в зависимости от показателя адиабаты (для воздуха k = 1,4).

9. Действительный процесс истечения сопровождается увеличением энтропии и температуры Т_2д (рис. 4). Действительная скорость истечения (W_2д, м/с) при этом также уменьшается и может быть найдена:

по действительному теплоперепаду Δh_д, кДж/кг

;

по действительному расходу воздуха через сопло G_д, кг/с

,

где ρ_с – плотность воздуха на выходе из сопла, которая находится по уравнения состояния воздуха в устье сопла, кг/м³; F_с - площадь выходного сечения сопла, м² (диаметр сопла равен 2,15 мм).

10. Коэффициент потери скорости находится по соотношению:

.

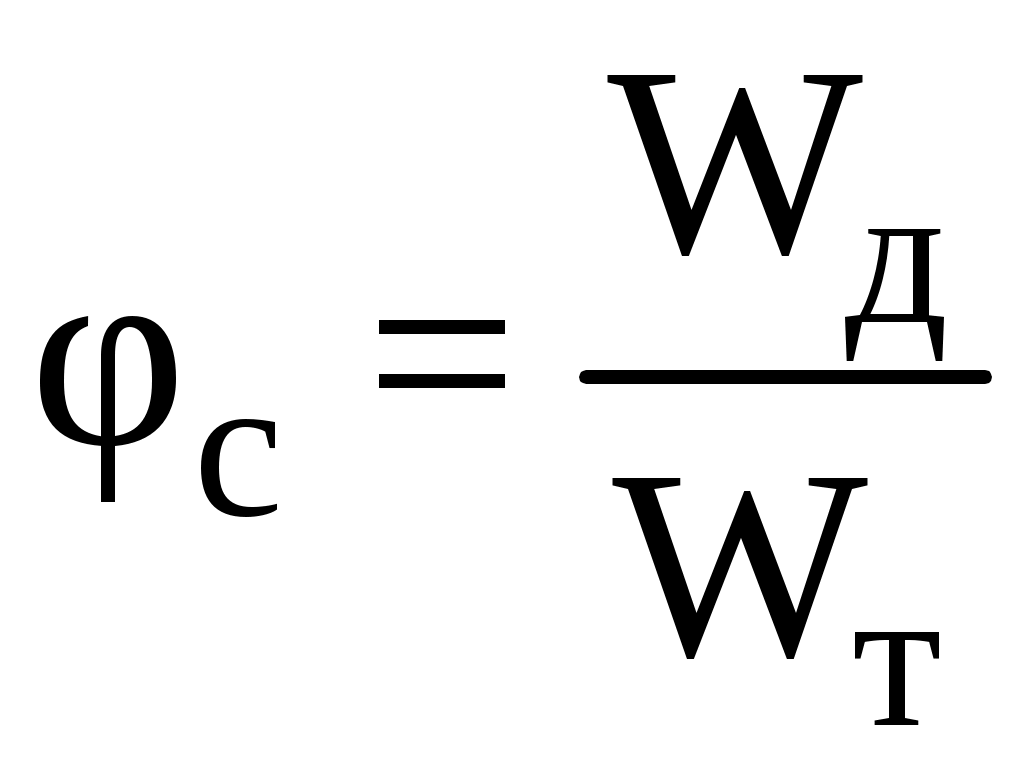11. Коэффициент потери энергии: .

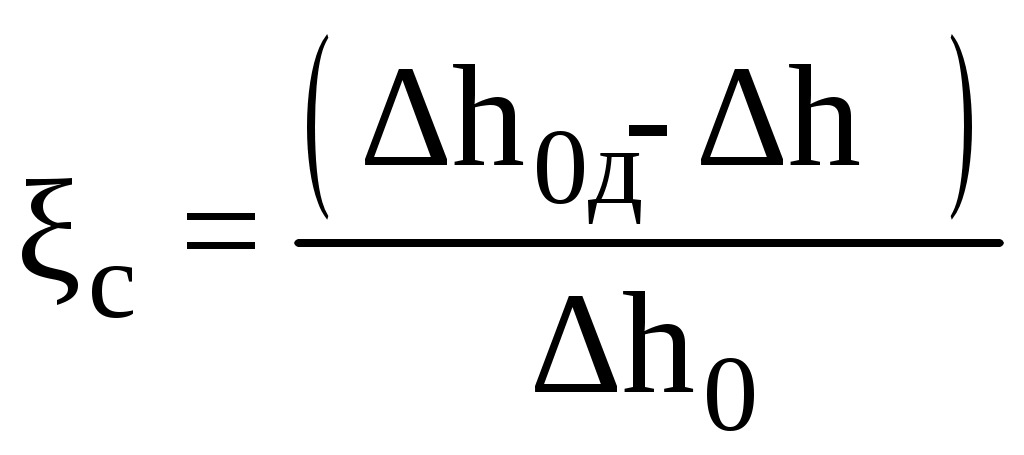12. Коэффициент полезного действия канала находится по соотношению: .

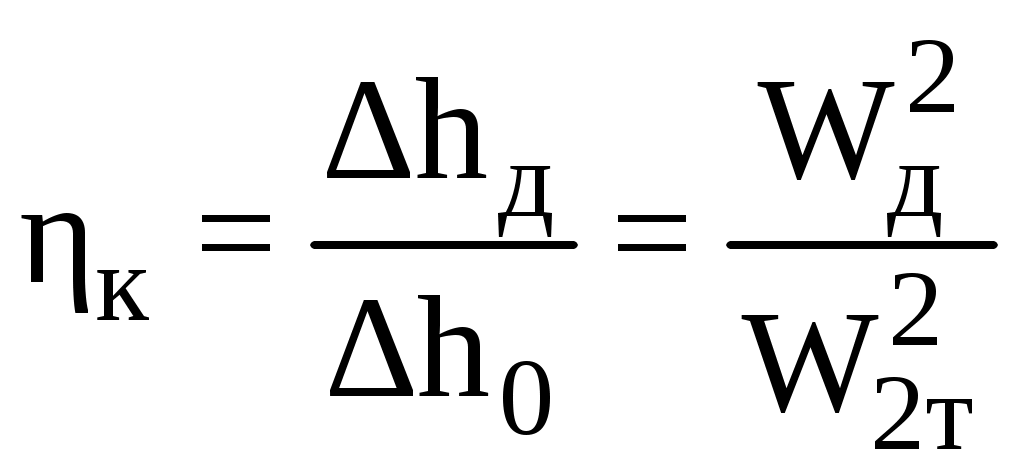Протокол результатов

Таблица 2.

№ п/п	Измеряемая величина	Обозна- чение	Номера опытов
			1	2	3	4	5	6	7	8	9	10	11	12
1	Атмосферное давление, бар	Ратм
2	Давление перед диафрагмой, бар	Р
3	Давление перед соплом, бар	Р1
4	Давление в выходном сечении сопла, бар	Р2'
5	Давление за соплом, бар	Р2
6	Табличное отношение давлений	βтабл
7	Расчетное отношение давлений	βрасч
8	Перепад давления на диафрагме, Па	ΔР
9	Плотность воздуха перед диафрагмой, кг/м3	ρ
10	Действительный расход воздуха, кг/ с	Gд
11	Теоретическая температура в выходном сечении сопла, К	Т2
12	Действительная температура в выходном сечении сопла, К	Т2д
13	Теоретическая скорость истечения, м/с	W2
14	Действительная скорость истечения, м/с	W2д
15	Коэффициент потери энергии	ζс
16	Коэффициент потери скорости	φc
17	Коэффициент полезного действия канала	ηк

1   2   3   4   5   6   7   8

---

Смотрите также файлы

• Робототехника блімі бойынша тапсырмалар.docx

• Правовое регулирование социального обслуживания граждан.rtf

• Задача 2 (ук10, У2).doc

• Реферат дисциплина Газовые турбины Задание выдано 2023 г.docx

• Отчет по преддипломной практикЕ (вид практики) Преддипломная практика (тип практики) 7 семестр.docx