Файл: Гл. 4 Сложение волн 1 Волновые пакеты 1). Бигармоническая волна 2).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 11
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Гл.4 СЛОЖЕНИЕ ВОЛН
§ 4.1 Волновые пакеты (4.1.1).
Бигармоническая волна (4.1.2)
4.1.1.
Гармоническая волна – идеальная модель. Процесс происходит за конечное время и формируется в ограниченном пространстве.
В соответствии с принципом суперпозиции произвольную волну в линейной среде можно представить в виде группы (гармонических!) волн или волнового пакета.
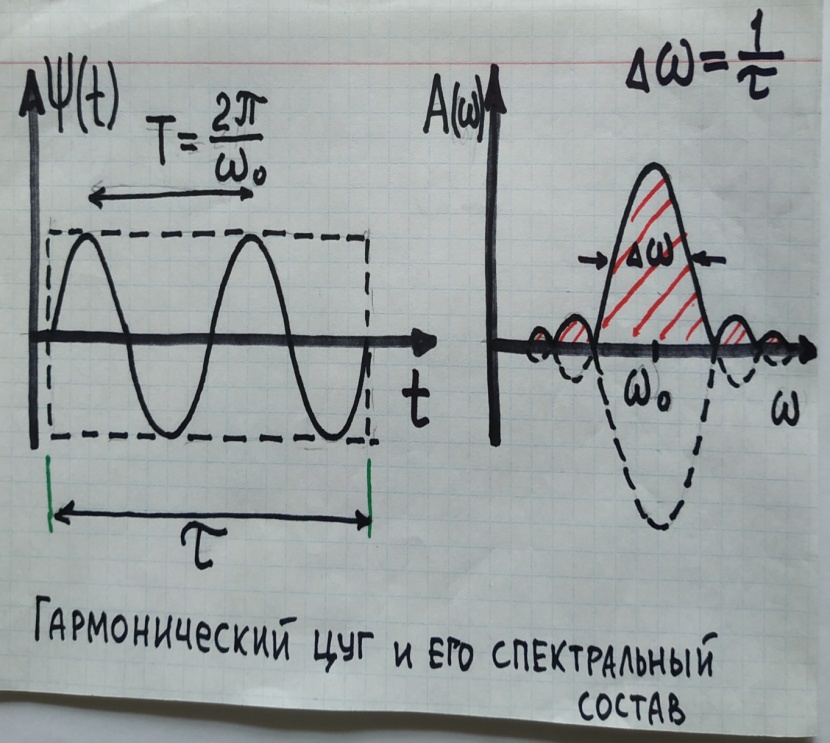
Пример такого пакета – гармонический цуг со сложной спектральной плотностью амплитуды А(ω) = Аω dω.
( А(k) = Ak dk )
Временной и пространственный спектры оказываются идентичными при отсутствии дисперсии. В силу преобразования Фурье формы огибающих спектра и цугов взаимно обратимы.
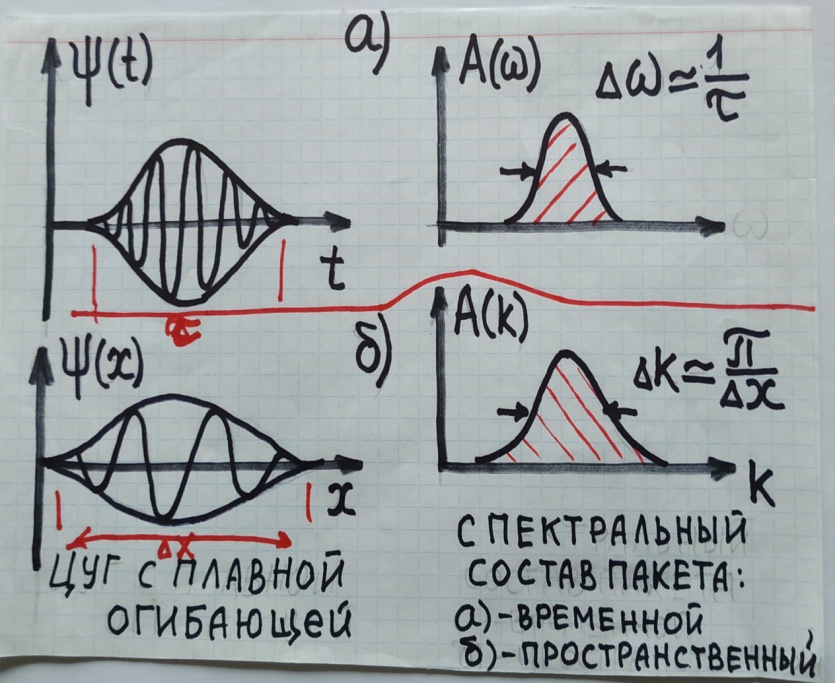
Также в силу того, что фазовые скорости волн, образующих пакет, одинаковы, его форма сохраняется. В противном случае, когда υ = f (ω),
волновой импульс “расплывается”.
4.1.2. Бигармоническая волна
Рассмотрим пространственный пакет из двух близких волн, когда:
А1 = А2 = А; ω1 = ω – dω, ω2 = ω + dω; k1 = k – dk , k2 = k + dk
Итак:
Ψ1 (x,t) = А1 cos [(ω – dω)t – (k – dk)x]
Ψ2 (x,t) = А2 cos [(ω + dω)t – (k +dk)x]
Используя формулу cos α + cos β = 2 cos
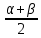 cos
cos 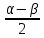 , получаем, пренебрегая бесконечно малыми
, получаем, пренебрегая бесконечно малымиΨ (x,t) = Ψ1 + Ψ2 =
= 2А cos (tdω - xdk) cos (ωt -kx)
Имеем в итоге амплитудно - модулированную гармоническую волну.
Ψ
(t) представляет процесс, называемый биениями с периодом Тмод. =
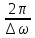 .
.§ 4.2 Групповая скорость. Соотношения
Рэлея
Скорость переноса центра нашего пакета (максимальной амплитуды Аm = 2А) находят дифференцированием из условия
(tdω - xdk) = const = 0
и называют её групповой
υг =
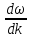
Связь между фазовой и групповой скоростью дана Рэлеем
υг =
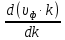 = υф +k
= υф +k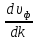
или
υг = υф - λ
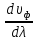 ,
,если учесть, что:
k =
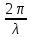 , dk = -
, dk = - 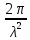 dλ
dλИтак, формулы Рэлея:
| υг = υф + k 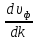 (4.1) υг = υф – λ 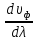 |
Они получаются и для многоволнового пакета.
§ 4.3 Соотношение неопределённости
для волн
Для волнового пакета с набором волн с частотами ω(k) и волновыми числами из интервала k -
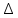 k, k +
k, k +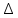 k, описываемого функцией
k, описываемого функциейΨ (x,t) =
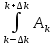 (k) cos [ω(k)∙t – kx] dk
(k) cos [ω(k)∙t – kx] dkамплитуда превращается в нуль, когда сдвиг по фазе каждой волны относительно волны суперпозиции достигает
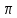 .
.
Значения огибающей пакета за пределами
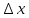
 /
/ k будут незначительными.
k будут незначительными.Таким образом, соотношениями определяющими область локализации пакета являются
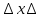 kx kx 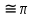 , , 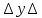 ky ky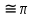 , , (4.2) 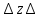 kz kz 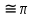 |
Чем меньше область локализации пакета, тем больше разброс волновых чисел и наоборот.
Данную связь называют соотношением неопределённости для волн.
Аналогичное соотношение характеризует временную локализацию пакета и носит название теоремы о ширине полосы частот
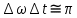 (4.3) (4.3) |
Уменьшение временной длительности пакета (
 t) приводит к расширению частотного спектра гармонических волн, формирующих заданный импульс.
t) приводит к расширению частотного спектра гармонических волн, формирующих заданный импульс.Фурье – разложение пакета по частотам имеет вид:
Ψ (x,t) =
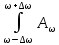 (ω) cos [ωt – k(ω)∙x] dω
(ω) cos [ωt – k(ω)∙x] dωПри нормальной дисперсии волны с более высокими частотами распространяются с меньшими фазовыми скоростями, что приводит к размытию пакета.
§ 4.4 Круговая и эллиптическая
поляризация как результат
сложения двух векторных волн
Рассмотрим суперпозицию двух гармонических линейно поляризованных плоских и взаимно-перпендикулярных волн
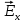 (z,t) =
(z,t) = 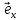 Exocos (ωt – kz + α)
Exocos (ωt – kz + α)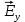 (z,t) =
(z,t) = 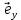 Eyocos (ωt – kz)
Eyocos (ωt – kz)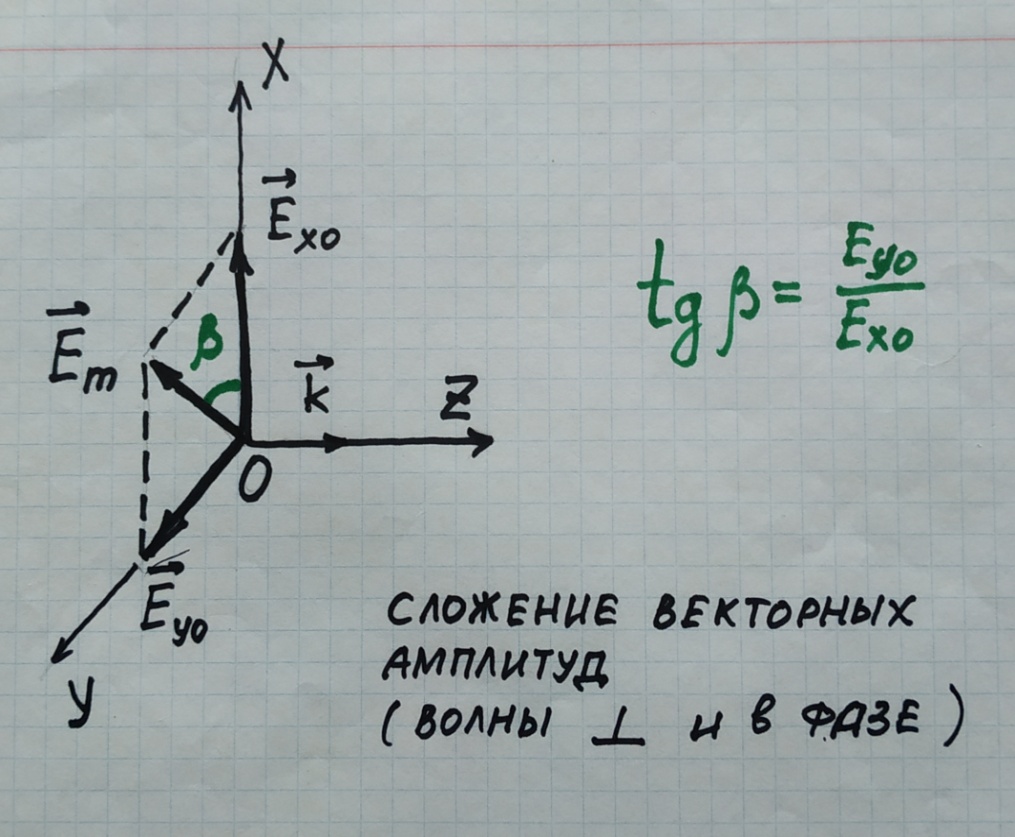
Если α = 0, то векторная сумма – плоская волна с амплитудой
Em =
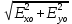
Направление колебаний волны составляет с осью 0Х угол β, причём
β = arc tg (
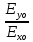 )
) Если угол α = +
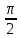 , тогда:
, тогда: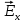 (z,t) =
(z,t) = 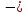
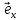 Exosin (ωt – kz)
Exosin (ωt – kz)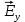 (z,t) =
(z,t) = 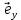 Eyocos (ωt – kz)
Eyocos (ωt – kz)и соответственно:
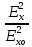 +
+ 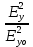 = 1
= 1Это уравнение эллипса, который в сечении z = 0 вычерчивает конец результирующего вектора
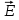 , вращающегося против часовой стрелки с угловой скоростью ω. При α = -
, вращающегося против часовой стрелки с угловой скоростью ω. При α = - 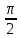 вращение будет по часовой стрелке.
вращение будет по часовой стрелке. Наконец, если Exo= Eyo =Eo вместо эллипса вычерчивается круг. (Говорят соответственно о “левой” или “правой” эллиптических и о “круговой” поляризациях волны.
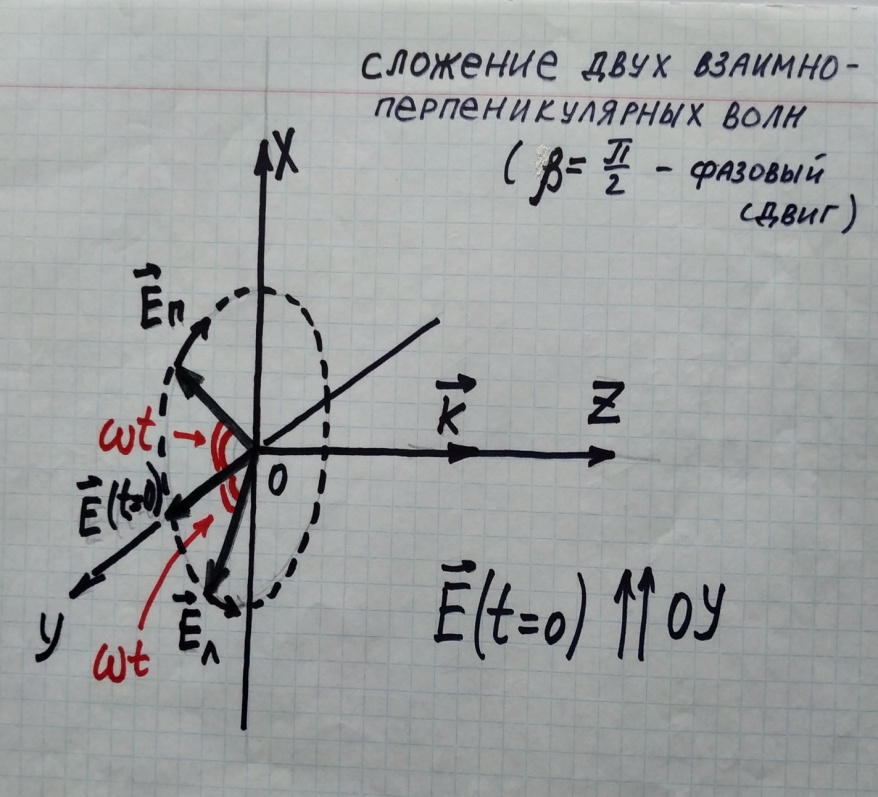
Таким образом из двух взаимно-перпендикулярных волн можно сформировать волну любой поляризации.
Интесивность волн неполяризованного (естественного) света I(φ) одинакова по всем направлениям. Для частично поляризованного света вводят величину η, определяющую степень его поляризации
η =
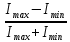 .
.