СТАТИСТИЧЕСКИЕ МЕТОДЫ В АДМИНИСТРАТИВНО-ГОСУДАРСТВЕННОМ УПРАВЛЕНИИВариант № 1

1. 
   Структурные средние.
   

При расчете средней величины индивидуальные значения заменя­ются одним средним значением. В ве­личине средней проявляется типичный размер признака, свойствен­ный данной группе или совокупности в целом.При расчете средней величины численность единиц совокупности должна быть достаточно большой. Средняя величина всегда именованная, она имеет ту же единицу измерения, что и признак у отдельных единиц совокупности. В экономических исследованиях применяются две категории средних:

• 
  Степенные средние;
  
• 
  Структурные средние – к ним относятся мода и медиана.
  

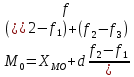
Мода — это наиболее часто встречающееся значение признака в совокупности. В интервальных вариационных рядах сначала находят модальный интервал.В найденном модальном интервале конкретное значение моды определяют по формуле:Где  - нижняя граница модального интервала; d— величина интервала;   - частоты предмодального, модального и посмодального интервалов.Мода широко применяется в коммерческой деятельности.Медиана — значение признака, находящееся посредине рассматри­ваемого ряда. Она указывает центр распределения единиц совокупно­сти и делит ее на две равные части.При отыскании медианы сначала определяется ее порядковый номер в ряду распределения.При нечетном числе единиц в ряду: При четном числе единиц в ряду:Т.е. 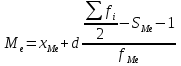полусумма из двух соседних центральных значений.ёВ интервальном ранжированном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором определяется конкретное значение медианы по формуле: Где 

---

 - нижняя граница медианного интервала;   - величина интервала;  частота, накопленная да медианного интервала;  - частота медианного интервала.

Медиана используется при контроле качества продукции и технологического процесса на промышленных предприятиях, при изучении распределения домохозяйств по величине дохода и т. д.

Мода и медиана имеют преимущества перед средними арифметическими для ряда распределения с открытыми интервалами.

2. 
   Методы исчисления валового внутреннего продукта.
   

ВВП - рыночная стоимость всех конечных товаров и услуг, произведённых за год во всех отраслях экономики на территории государства для потребления, экспорта и накопления.Номинальный ВВП (абсолютный)— выражен в текущих ценах данного года.Реальный ВВП (с поправкой на инфляцию) — выражен в ценах предыдущего или любого другого базового года. В реальном ВВП учитывается, в какой степени рост ВВП определяется реальным ростом производства, а не ростом цен.Дефлятор ВВП – ценовой индекс, созданный для измерения общего уровня цен на товары и услуги, находящийся как отношение номинального ВВП к реальному.Фактический ВВП — это ВВП при неполной занятости — это ВВП, который отражает реализованные возможности экономики.Потенциальный ВВП — это ВВП при полной занятости. Это ВВП, который будет отражать потенциальные возможности экономики. Потенциальные возможности экономики могут быть намного выше реальных.Для расчета ВВП может быть использовано три метода:

1. 
   по доходам: суммируются доходы населения, корпораций, проценты по сбережениям, доходы государства от предпринимательской деятельности, а также в виде налогов на производство и импорт, амортизационные отчисления;
   
2. 
   по расходам: суммируются потребительские расходы домашних хозяйств, инвестиционные расходы фирм, государственные расходы на закупки товаров, услуги и инвестиции и сальдо внешней торговли;
   
3. 
   по сумме произведенной продукции: суммируются только добавленные каждой фирмой стоимости.
   

---

Использование этих методов даёт одинаковый результат, поскольку в экономике совокупный доход равен величине совокупных расходов, а величина добавленной стоимости равна стоимости конечной продукции, при этом величина стоимости конечной продукции есть не что иное, как сумма расходов конечных потребителей на покупку совокупного продукта.

3. 
   Задача.
   

По 6 предприятиям отрасли известны следующие данные:

Номер предприятия	Объем потребления электроэнергии, кВт ч	Выпуск продукции, тыс. шт.
1 2 3 4 5 6	12,3 11,7 10,9 12,0 20,7 13,7	38 26 46 48 51 52

С помощью коэффициентов ранговой корреляции Спирмена и Фехнера оцените тесноту связи между указанными признаками.Коэффициент ранговой корреляции Спирмена.Присвоим ранги признаку Y и фактору X.

X	Y	ранг X, dx	ранг Y, dy
12.3	38	4	2
11.7	26	2	1
10.9	46	1	3
12	48	3	4
20.7	51	6	5
13.7	52	5	6

Матрица рангов.

ранг X, dx	ранг Y, dy	(dx - dy)2
4	2	4
2	1	1
1	3	4
3	4	1
6	5	1
5	6	1
21	21	12

---

Проверка правильности составления матрицы на основе исчисления контрольной суммы:Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.По формуле вычислим коэффициент ранговой корреляции Спирмена. Связь между признаком Y и фактором X умеренная и прямаяОценка коэффициента ранговой корреляции Спирмена.Значимость коэффициента ранговой корреляции СпирменаДля того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе H_i. p ≠ 0, надо вычислить критическую точку:где n - объем выборки; p - выборочный коэффициент ранговой корреляции Спирмена: t(α, к) - критическая точка двусторонней критической области, которую находят по таблице критических точек распределения Стьюдента, по уровню значимости α и числу степеней свободы k = n-2.Если p < Т_kp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками не значима. Если p > T_kp - нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.По таблице Стьюдента находим t(α/2, k) = (0.05/2;4) = 3.495Вывод:Коэффициент корреляции Спирмена (ρ) равен 0,657Связь между исследуемыми признаками - прямая, теснота (сила) связи по шкале Чеддока - заметнаяЧисло степеней свободы (f) составляет 4Критическое значение критерия Спирмена при данном числе степеней свободы составляет 0,886.Поскольку Tkp > p, то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена.

---

Ρ набл < Ρ крит, зависимость признаков статистически не значима (p > 0,05)Коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:где n_a - число совпадений знаков отклонений индивидуальных величин от средней; n_b - число несовпадений.Коэффициент Фехнера может принимать значения от –1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф = -1 свидетельствует о возможном наличии обратной связи.Расчет коэффициента Фехнера по данным, приведенным в таблице:Средние значения:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
12.3	38	-	-	A
11.7	26	-	-	A
10.9	46	-	+	B
12	48	-	+	B
20.7	51	+	+	A
13.7	52	+	+	A
81.3	261

Значение коэффициента свидетельствует о том, что можно предполагать наличие прямой связи.Оценка коэффициента корреляции знаков. Значимость коэффициента Фехнера.

---

Смотрите также файлы

• Курсовая работа Анализ видов исследований проводимых при пенокислотной обработке.docx

• Лабораторная работа 2 по дисциплине (учебному курсу) физика.docx

• Введение Гора Олимп на Марсе.docx

• Курсового проекта Способы съема акустической (речевой) информации за пределами контролируемой зоны кп. 420200. 10. 03. 01. Пз.docx

• Жалпы физика курсы бойынша есептер жинаы растыран Мырзабекова Г. Б. Шымкент 2019ж. азастан.docx