1.7. Какую сумму S0 нужно положить на депозит под i % годовых, чтобы через n лет при "m"-кратном начислении сложных процентов получить сумму Sn тыс. рублей? (Значение S0 определить с точностью до копеек).

Цифра № по списку	2
i%	9,2
m	4
n лет	2,5
Sn (тыс. руб.)	280

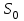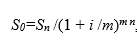
Решение:Для случая начисления процентных доходов по схеме сложных процентов приведенная современная величина определяется формулой. При m-кратном начислении процентов математическое дисконтирование определяется формулойПосле подстановки числовых значений в эту формулу получим: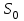= 280 000/(1 + 0,092/4)^2,5*4 = 223049,73 руб.1.13. В банк положен депозит на один год c выплатой процентов в конце года под i % годовых. Определить реально действующую (эффективную) iэф % процентную ставку с учетом выплаты налога НДФЛ при ставке налога gн=35 % и ключевой ставке ЦБ России iцб.

Цифра № по списку	2
i%	13,5
iцб %	7,8

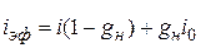
Решение:Iэф=0,135*(1-0,35)+0,35*(0,078+0,05)=13,26%6.12. Определите дюрацию портфеля облигаций с характеристиками, приведенными в условии задачи 6.10. Портфель облигаций состоит из двух видов облигаций с характеристиками, приведенными в таблице. Определить суммарную рыночную стоимость "V∑" портфеля облигаций, если число облигаций первого вида равно q1=10 а второго вида q2=20.

---

Цифра № по списку	2
PN1 (тыс. руб.)	3
с1	0,07
ρ1	0,08
n1 лет	2
PN2 (тыс. руб.)	7
с2	0,04
ρ2	0,12
n2 лет	4

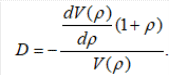
Решение:Определим рыночную стоимость облигации первого вида по формулеV1=3000*(0,07*(1-(1,08)^-2/0,08+(1,08)^-2)= 2946,50 руб.Аналогично определяем рыночную стоимость облигации второго вида:V2=7000*(0,04*(1-(1,12)^-4/0,12+(1,12)^-4)=5299,09 руб.Для суммарной рыночной стоимости портфеля облигаций получим: Vсум =q1 x V1 + q2 x V2 =10 x 2946,5 + 20 x 5299,09 =135 446,8 руб.D1=1,08/0,08-(2*(0,07-0,08)+1+0,08)/(0,07*(1+0,08)²-1)+0,08)=1,93D2=1,12/0,12-(4*(0,04-0,12)+1+0,12)/(0,04*(1+0,12)⁴-1)+0,12)=3,74Dп=1,93*2946,50+3,74*5299,09/135446,8=0,197.10. По данным таблиц коммутационных функций определить значение коэффициента приведения m|ax:n| для отложенного на m лет ограниченного сроком n лет страхового аннуитета постнумерандо с началом выплат в возрасте страхуемого x лет при годовой процентной ставке доходности i=4,5 %.

Цифра № по списку	2
x	40
m	11
n	20

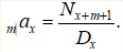
Решение:При m = 11 и n = 20 лет получим: 7.23. По таблицам коммутационных функций рассчитать размер ежегодных накопительных платежей, при которых ежегодные пенсионные выплаты составят R тысяч рублей. Расчет провести для годовой процентной ставки доходности i = 4,5 % для случаев отложенного пожизненного пенсионного страхования и отложенного ограниченного сроком n лет пенсионного страхования мужчины в возрасте x лет при его выходе на пенсию в возрасте L лет.

---

Цифра № по списку	2
R т. руб.	28
x	43
L	62
n	21

Решение:Ax = R ax =R (Nx+1/Dx) = 28000 (407014,8/26004,0) = 438 256,21 руб.Ax*=R ax*= R(Nx/Dx) = 28000(433018,9/26004,0) = 466 256,31 руб.При n = 21 летAx:n| = R ax:n|= R (Nx+1 – Nx+n+1) / Dx==28000(407014,8– 80048,6) /26004,0=352 063,28 руб.Ax:n|*= R ax:n|*=R(Nx– Nx+n) / Dx ==28000(433018,9– 88386,9) /26004,0=371 085,06 руб.

---

Смотрите также файлы

• Тема Развитие творческих способностей у детей младшего дошкольного возраста через использование современной техники рисования Скетчинг через проектную деятельность.docx

• Межгосударственный стандарт межгосударственная система стандартизации стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации общие требования к построению, изложению, оформлению, содержанию и обозначению.rtf

• Практическая работа по дисциплине Методы и средства проектирования информационных систем и технологий Унифицированный язык моделирования (uml). Диаграмма вариантов использования системы.pdf

• Лекция Гендерные исследования лидерства Задание.docx

• Опасное событие Заболевания кожи (дерматиты) Меры управленияконтроля профессиональных рисков.docx