Файл: Курсовой проект по дисциплине Идентификация и диагностика систем.rtf

температура окружающего воздуха, ºC	20 ± 5
температура воды в охлаждающем контуре горячих спаев, ºС	15 ± 10
относительная влажность окружающего воздуха, %	30 − 80
атмосферное давление, кПа	84,0 – 106,7
напряжение питания, В	220 ± 10

Расчет параметров модели Ко и То при режиме охлаждения

Представленные ниже экспериментальные переходные характеристики объекта h(t) табл.1 с достаточной точностью могут быть аппроксимированы экспоненциальной зависимостью:



где K₀ – коэффициент передачи, Т₀ – постоянная времени объекта на рис.4.

Такая временная характеристика соответствует линейной математической модели в виде передаточной функции типового апериодического (инерционного) звена:
W₀(p)=
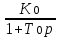
с достаточно большой инерционностью Т₀ = 1000 – 5000 с, которую можно оценить моментом времени с координатой h(T₀) = 0.63 h_уст, где h_уст – установившееся значение h(t) при t→ ∞.

Коэффициент передачи объекта определяется согласно выражению
К_О=∆t°/∆U,
где ∆U - приращение входного воздействия, ∆t°– соответствующее приращение выходного сигнала. По экспериментальным данным определено К₀=11К/В. Постоянная времени Т₀=4200 с.


Расхождения между экспериментальными данными h(t) и теоретическими, определенными по модели, не превышают 8,6%.

Результаты расчета в табличном и графическом виде представлены в табл. 1 и графике рис. 5.


Табл.1

Время, с	Температура, С°	∆t	∆T	H(t)	∆i	δi
15360	-9,2	0	0	0,00	0,00	0,0%
15600	-9,2	240	0	-0,61	0,61	5,9%
15840	-9,5	480	-0,3	-1,19	0,89	8,6%
16080	-10,2	720	-1	-1,73	0,73	7,1%
16320	-10,8	960	-1,6	-2,25	0,65	6,3%
16560	-11,4	1200	-2,2	-2,73	0,53	5,2%
16800	-11,9	1440	-2,7	-3,19	0,49	4,8%
17040	-12,5	1680	-3,3	-3,63	0,33	3,2%
17280	-12,9	1920	-3,7	-4,04	0,34	3,3%
17520	-13,4	2160	-4,2	-4,42	0,22	2,2%
17760	-13,8	2400	-4,6	-4,79	0,19	1,8%
18000	-14,2	2640	-5	-5,13	0,13	1,3%
18240	-14,5	2880	-5,3	-5,46	0,16	1,5%
18480	-14,8	3120	-5,6	-5,77	0,17	1,6%
18720	-15,2	3360	-6	-6,06	0,06	0,6%
18960	-15,5	3600	-6,3	-6,33	0,03	0,3%
19200	-15,7	3840	-6,5	-6,59	0,09	0,9%
19440	-16	4080	-6,8	-6,84	0,04	0,3%
19680	-16,2	4320	-7	-7,07	0,07	0,7%
19920	-16,5	4560	-7,3	-7,29	0,01	0,1%
20160	-16,7	4800	-7,5	-7,49	0,01	0,1%
20400	-16,9	5040	-7,7	-7,69	0,01	0,1%
20640	-17,1	5280	-7,9	-7,87	0,03	0,3%
20880	-17,2	5520	-8	-8,04	0,04	0,4%
21120	-17,4	5760	-8,2	-8,21	0,01	0,1%
21360	-17,6	6000	-8,4	-8,36	0,04	0,4%
21600	-17,7	6240	-8,5	-8,51	0,01	0,1%
21840	-17,8	6480	-8,6	-8,65	0,05	0,5%
22080	-18	6720	-8,8	-8,78	0,02	0,2%
22320	-18,1	6960	-8,9	-8,90	0,00	0,0%
22560	-18,2	7200	-9	-9,02	0,02	0,2%
22800	-18,3	7440	-9,1	-9,13	0,03	0,3%
23040	-18,4	7680	-9,2	-9,23	0,03	0,3%
23280	-18,5	7920	-9,3	-9,33	0,03	0,3%
23520	-18,6	8160	-9,4	-9,42	0,02	0,2%
23760	-18,7	8400	-9,5	-9,51	0,01	0,1%
24000	-18,8	8640	-9,6	-9,59	0,01	0,1%
24240	-18,8	8880	-9,6	-9,67	0,07	0,7%
24480	-18,9	9120	-9,7	-9,75	0,05	0,4%
24720	-19	9360	-9,8	-9,82	0,02	0,2%
24960	-19,1	9600	-9,9	-9,88	0,02	0,2%
25200	-19,1	9840	-9,9	-9,94	0,04	0,4%
25440	-19,2	10080	-10	-10,00	0,00	0,0%
25680	-19,3	10320	-10,1	-10,06	0,04	0,4%
25920	-19,3	10560	-10,1	-10,11	0,01	0,1%
26160	-19,4	10800	-10,2	-10,16	0,04	0,4%
26400	-19,4	11040	-10,2	-10,21	0,01	0,1%
26640	-19,5	11280	-10,3	-10,25	0,05	0,5%
26880	-19,5	11520	-10,3	-10,29	0,01	0,1%
27120	-19,6	11760	-10,4	-10,33	0,07	0,7%

---

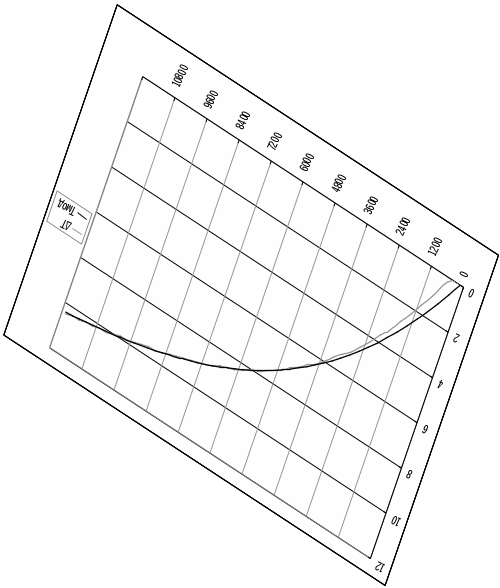
Рис. 5
3. Сравнительный анализ исходных данных и результатов моделирования

компьютерное моделирование термический математический

Отклонение между экспериментальными данными и результатами моделирования можно вычислить по формуле
δ_max=∆_i/h_max,
где ∆_i=│h_экс(t_i)−h_мод(t_i)│.

Значение δ_max=8.6% (табл. 1). Для нас это приемлемое отклонение. Для тех случаев, когда необходимо получить меньшее значение δ_max, можно рекомендовать проведение режима параметрической оптимизации.

В программном пакете «КАЛИСТО» набор поисковых алгоритмов для решения задач оптимизации включает алгоритмы:

• 
  Гаусса-Зейделя;
  
• 
  Розенброка;
  
• 
  Симплексного метода.
  

Процедура параметрической оптимизации осуществляет поиск и определение параметров передаточной функции, обеспечивающих в заданном диапазоне максимальную близость смоделированной и желаемой характеристик. Для проведения этой процедуры в ПП «КАЛИСТО» необходимо после расчета h(t)_мод ввести в ПК следующую информацию:

1. 
   Пункт меню “Параметры”: на наборном поле нужно указать блок, параметры которого должны изменяться, затем в окне параметров отметить сами оптимизируемые параметры (максимальное число оптимизируемых параметров -5);
   
2. 
   Пункт меню “Метод”: указать выбранный метод оптимизации (Розенброка, Гаусса-Зейделя или симплексный);
   
3. 
   Пункт меню “Пределы”: задать диапазон изменения выбранных в п. 1 параметров, их минимальное и максимальное значения и задать шаг поиска оптимального значения по каждому параметру;
   
4. 
   Пункт меню “Желаемая характеристика”: а) уточнить при необходимости масштаб графика по осям х и у ; б) нанести на рассчитанный график h(t) _мод точки с желаемыми координатами (максимальное число таких точек -100); точки должны вводиться последовательно с увеличением значения по оси х;
   
5. 
   Пункт меню “Кол. шагов”: задать количество шагов в итерационной процедуре – условие прекращения поиска оптимальных значений параметров.
   

После задания этой информации и расчета новой характеристики найденные оптимальные параметры автоматически записываются в исходную модель. При необходимости можно повторить режим поиска, взяв за начальные те значения изменяемых параметров, которые были рассчитаны при предыдущей попытке оптимизации. Поле для проведения режима параметрической оптимизации приведено на рис.6.

---

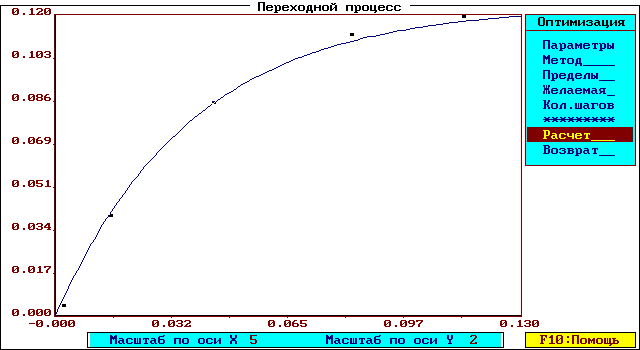
Рис.6.

Как было отмечено ранее, особым преимуществом термоэлектрических устройств является то, что изменением полярности питания такого устройства можно регулировать температуру как выше, так и ниже температуры окружающей среды.

4. Анализ устойчивости и качества замкнутой САУ
Температурный датчик, используемый в эксперименте, представляет собой апериодическое звено с передаточной функцией
.
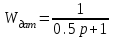Закон управления – пропорционально-интегральный, поэтому
.
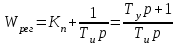Передаточная функция разомкнутой цепи:
.
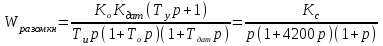Статическая ошибка при пропорционально-интегральном законе регулирования равна 0.

Пусть коэффициент передачи системы равен 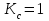, тогда .

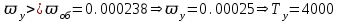Тогда

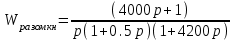
Проведем предварительно анализ устойчивости замкнутой системы по критерию Рауса-Гурвица.

Составим характеристический многочлен, который является суммой числителя и знаменателя передаточной функции разомкнутой системы, приравняем его к нулю:



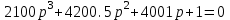
Для систем 3-го порядка необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения и то, что произведение средних двух коэффициентов многочлена больше произведения крайних. Таким образом, данная замкнутая система устойчива.

Построим асимптотические ЛЧХ (рис. 7).

Оценим критический коэффициент. Фазовая характеристика пересекает ось 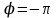на частоте , поэтому .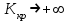

Запас устойчивости по фазе 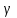порядка 60°. Запас устойчивости по амплитуде стремится к +∞. Это хорошие показатели, поэтому оставим К_с=1.

Частота среза 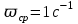, поэтому ожидаемое время регулирования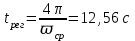

---

.
Однако, время регулирования может быть на самом деле в разы меньше, мы лишь оцениваем его порядок.



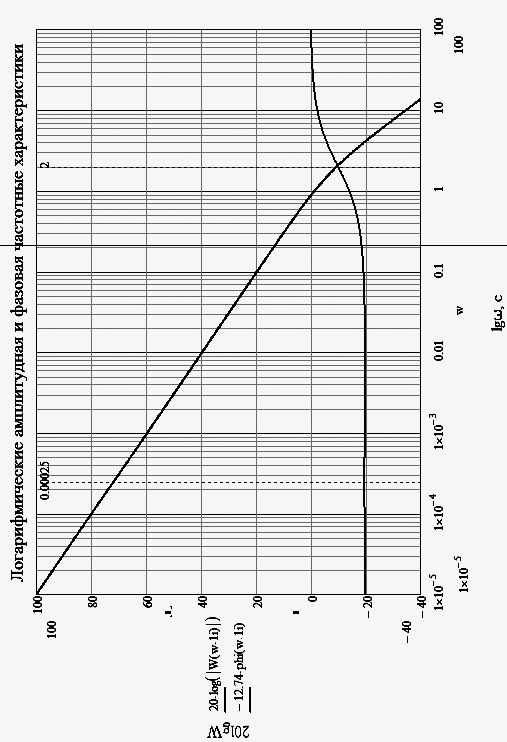
Рис. 7.
В контуре управления анализируемые системы содержат микропроцессорные устройства, работающие с дискретными сигналами, т.е. такие системы являются не непрерывными, а дискретно – непрерывными. Микропроцессорные устройства квантуют непрерывный сигнал и по уровню и по времени. Квантование по уровню происходит потому, что амплитуда дискретного сигнала ограничена некоторой совокупностью значений, определяемой разрядностью микропроцессора. Но квантование по уровню по сравнению с квантованием по времени создает на выходе эффект второго порядка малости, поэтому обычно при рассмотрении динамики системы в первом приближении квантованием по уровню пренебрегают.

Анализируя влияние квантования сигнала по времени и сравнивая период дискретизации сигнала 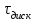и величину постоянных времени объекта управления 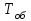, можно определенно сказать, что исследуемую систему следует рассматривать как непрерывную, так как > .

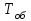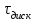Структурная математическая модель непрерывной системы управления термическим оборудованием с пропорциональным законом регулирования показана на рисунке ниже.

Рассчитаем переходную характеристику замкнутой САУ с помощью ПП «МОДОС». Для этого построим в программе модель системы, состоящую из источника сигнала, сумматора, интегратора, упругого и апериодического звеньев с коэффициентами многочленов: для источника - 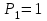, для сумматора - 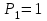, , 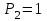, 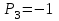для усилителя Р₁=1, для интегратора - ,

---

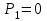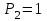
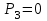, , для упругого звена - 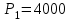, , 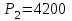для апериодического звена - , .

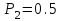Обозначаем выходы системы. Схема моделирования изображена на рис. 8.

Параметры интегрирования: метод Эйлера пропорциональный, время наблюдения 7с, шаг интегрирования 0,05с, интервал выдачи данных 0.07с.

Полученная переходная характеристика показана на рис. 9. Она имеет колебательный характер. Как и предполагалось, установившаяся ошибка 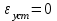. Время регулирования 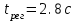. Перерегулирование равно 6%.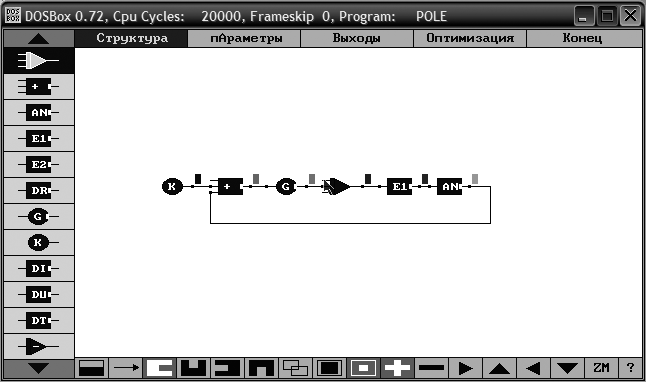


Рис. 8


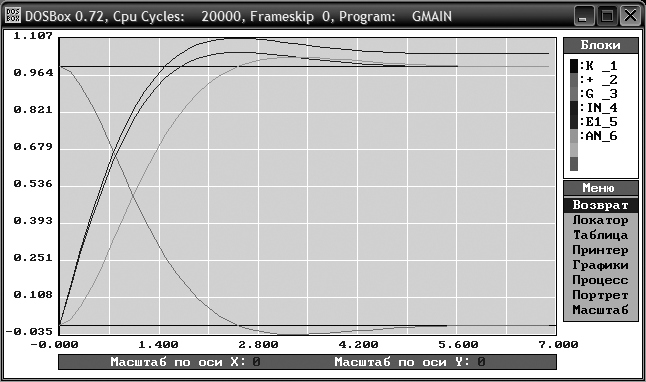
Рис. 9

5. Звено чистого запаздывания
Звено чистого запаздывания. Это звено без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время. Уравнение такого звена имеет вид:
где - время запаздывания.
Очевидно, характеристики этого звена будут:

Отсюда АФЧХ:

Передаточная функция:

В качестве примера звена можно назвать длинную электрическую линию без потерь, механический транспортер и т.д.

По существу, это звено относится к нелинейным. Однако при расчетах САУ с такими звеньями можно применять методы теории линейных систем. Поэтому часто элементы, закон движения которых мало изучен или трудно представим в аналитической форме, после некоторой идеализации представляются в виде звеньев запаздывания.

---