Файл: Тесты к экзамену по учебной дисциплине " Математика ".docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 45
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕСТЫ К ЭКЗАМЕНУ
по учебной дисциплине
"Математика "
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Составитель ст.пр. Обручева Т.С.
Санкт-Петербург
2013
| № | Вопросы | Варианты ответов | ||
| | ФУНКЦИОНАЛЬНЫЕ РЯДЫ | | ||
| | КАТЕГОРИЯ 1 | | ||
| | Какой из данных рядов является степенным рядом? | 1. 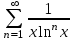 2. 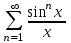 3. 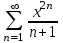 4. 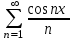 | ||
| | Степенной ряд 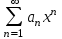 расходится при расходится при 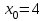 . Указать все значения x, при которых он расходится. (теор. Абеля) . Указать все значения x, при которых он расходится. (теор. Абеля) | | ||
| | Если R – радиус сходимости степенного ряда 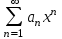 , то его интервал сходимости есть промежуток , то его интервал сходимости есть промежуток | 1. 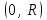 2. 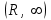 3. 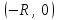 4. 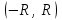 | ||
| | Если степенной ряд 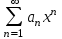 сходится при сходится при 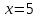 , то он сходится …. , то он сходится …. | 1.при всех 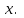 2. при всех 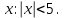 3. при всех 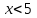 4. при всех 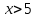 | ||
| | Теорема Абеля используется для исследования на сходимость | 1.знакочередующихся числовых рядов 2.положительных числовых рядов 3.функцональных рядов 4. только степенных рядов | ||
| | Как определяется радиус сходимости R степенного ряда 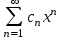 ? ? | 1. 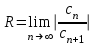 2. 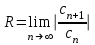 3. 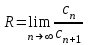 4. 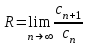 | ||
| | Степенной ряд 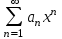 сходится при сходится при  . Указать все значения x, при которых он заведомо сходится абсолютно. (теорема Абеля) . Указать все значения x, при которых он заведомо сходится абсолютно. (теорема Абеля) | 1. 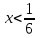 2. 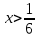 3. 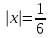 4. 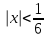 | ||
| | Укажите радиус и интервал сходимости степенного ряда 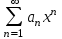 , если , если 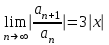 , то , то | 1. R= 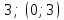 2. R= 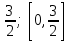 3. R= 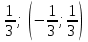 4. R= 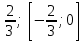 | ||
| | Указать радиус и интервал сходимости степенного ряда 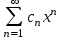 , если , если 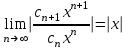 | 1. R=1, 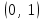 2. R=0 3. R=0, 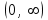 4. R= 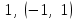 | ||
| | Указать разложение функции 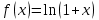 в ряд Маклорена в ряд Маклорена | | ||
| | Какая из приведенных формул определяет коэффициенты Тейлора функции 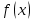 в точке в точке 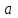 ? ? | 1. 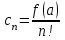 2. 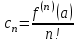 3. 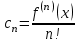 4. 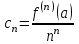 | ||
| | Указать ряд Тейлора для функции 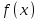 | 1.  2. 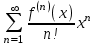 3. 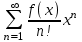 4. 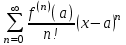 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 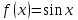 | 1. 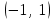 2. 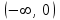 3. 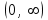 4. 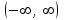 | ||
| | Какая функция раскладывается в ряд 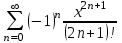 | 1. 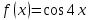 2. 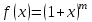 3. 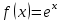 4.. 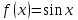 | ||
| | В каком промежутке можно почленно дифференцировать степенной ряд 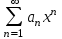 , если R — его радиус сходимости? , если R — его радиус сходимости? | | ||
| | Если R – радиус сходимости степенного ряда, то для определения области сходимости надо ли дополнительно исследовать поведение ряда в точках 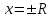 | 1.всегда 2.иногда 3.необязательно 4.не нужно | ||
| | Какая функция раскладывается в ряд 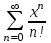 | 1. 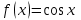 2. 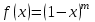 3. 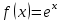 4. 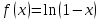 | ||
| | Какая функция раскладывается в ряд 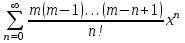 | 1. 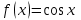 2. 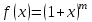 3. 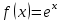 4. 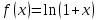 | ||
| | Какая функция раскладывается в ряд 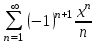 | 1. 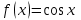 2. 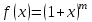 3. 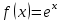 4. 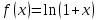 | ||
| | Какая функция раскладывается в ряд 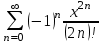 | 1. 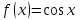 2. 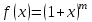 3. 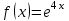 4. 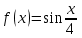 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 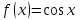 | 1. 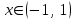 2. 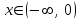 3. 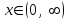 4. 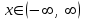 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 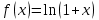 | 1. 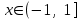 2. 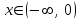 3. 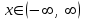 4. 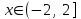 | ||
| | Указать разложение функции 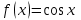 в ряд Маклорена в ряд Маклорена | | ||
| | Указать ряд Маклорена для функции 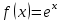 | | ||
| | Какие пределы можно брать для приближенного вычисления интеграла 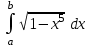 ? ? | 1. 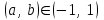 2. 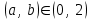 3. 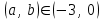 4. 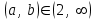 | ||
| | КАТЕГОРИЯ 2 | | ||
| | Если для ряда 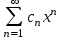 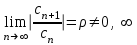 , , то его интервал сходимости | | ||
| | Если для ряда 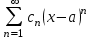 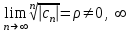 , , то его радиус сходимости 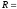 | | ||
| | Если степенной ряд 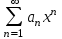 сходится при сходится при 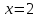 , то он сходится …. , то он сходится …. | 1.при всех 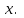 2. при всех 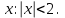 3. при всех 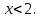 4. при всех 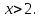 | ||
| | Степенной ряд 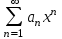 расходится при расходится при 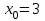 . Указать все значения x, при которых он расходится. (теор. Абеля) . Указать все значения x, при которых он расходится. (теор. Абеля) | 1. 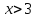 2. 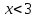 3. 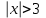 4. 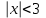 | ||
| | Степенной ряд 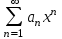 сходится при сходится при 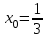 . Указать все значения x, при которых он заведомо сходится абсолютно. (теорема Абеля) . Указать все значения x, при которых он заведомо сходится абсолютно. (теорема Абеля) | 1. 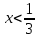 2. 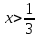 3. 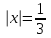 4. 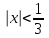 | ||
| | Укажите радиус и интервал сходимости степенного ряда 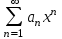 , если, , если, 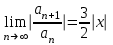 , , | 1. R= 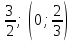 2. R= 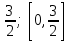 3. R= 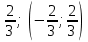 4. R= 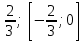 | ||
| | Указать радиус и интервал сходимости степенного ряда 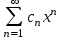 если если 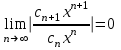 | 1. R=1, 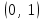 2. R=0 3. R=0, 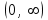 4. R= 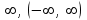 | ||
| | Указать радиус и интервал сходимости степенного ряда 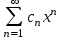 если если 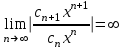 | 1. R=1, 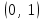 2. R=0 3. R=0, 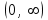 4. R= 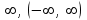 | ||
| | Указать ряд Маклорена для функции 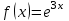 | 1. 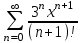 2. 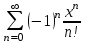 3. 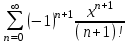 4. 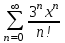 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 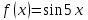 | 1. 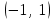 2. 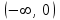 3. 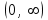 4. 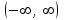 | ||
| | Какая функция раскладывается в ряд 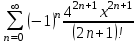 | 1. 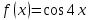 2. 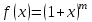 3. 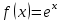 4.. 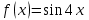 | ||
| | В каких пределах можно почленно интегрировать степенной ряд 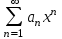 , если R — его радиус сходимости? , если R — его радиус сходимости? | | ||
| | Указать ряд Маклорена для функции 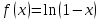 | 1. 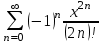 2. 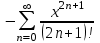 3. 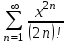 4. 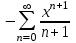 | ||
| | Какая функция раскладывается в ряд 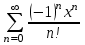 | 1. 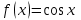 2. 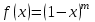 3. 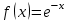 4. 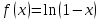 | ||
| | Какая функция раскладывается в ряд 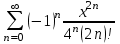 | 1. 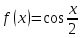 2. 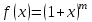 3. 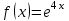 4. 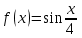 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 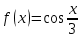 | 1. 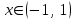 2. 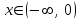 3. 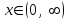 4. 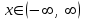 | ||
| | Дан ряд Тейлора 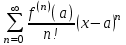 для функции для функции 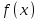 Напишите два первых члена ряда функции Напишите два первых члена ряда функции 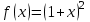 при при 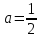 | 1. 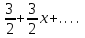 2. 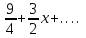 3. 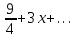 4. 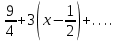 | ||
| | Дан ряд Тейлора 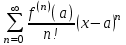 для функции для функции 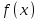 Напишите два первых члена ряда функции Напишите два первых члена ряда функции 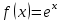 при при 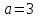 | 1. 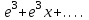 2. 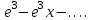 3. 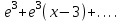 4. 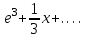 | ||
| | Указать промежуток сходимости ряда Маклорена для функции 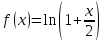 | 1. 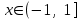 2. 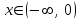 3. 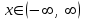 4. 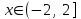 | ||
| | Какие пределы можно брать для приближенного вычисления интеграла 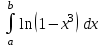 ? ? | | ||
| | Какие пределы можно брать для приближенного вычисления интеграла 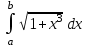 ? ? | 1. 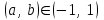 2. 2.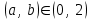 3. 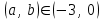 4. 4.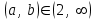 | ||
| | Данное свойство 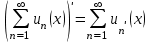 справедливо для справедливо для |
| ||
| | Данное свойство 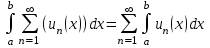 справедливо для | 1.знакочередующихся числовых рядов 2.знакопеременных рядов 3.положительных числовых рядов 4.равномерно сходящихся функциональных рядов | ||
| | При каком условии бесконечно дифференцируемая функция 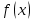 раскладывается в ряд Маклорена? раскладывается в ряд Маклорена? | 1. 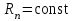 2. 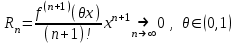 3. 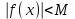 4. 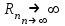 , Rn – остаточный член формулы Тейлора , Rn – остаточный член формулы Тейлора | ||
| | Какое из перечисленных условий является достаточным для сходимости ряда Тейлора к разлагаемой функции на промежутке 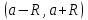 ? ? |
| ||
Составитель
ст.препод. Обручева Т.С.
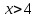
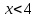
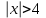
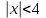
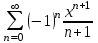
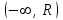
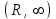
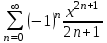
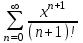
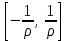
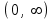
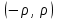
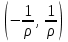

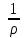
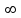
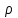
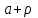
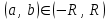
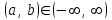
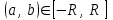
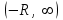
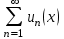 , для которого ряд
, для которого ряд 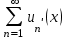 является равномерно сходящимся
является равномерно сходящимся