Файл: Контрольная работа на тему Теория графов Уктамбоев Куранбой Журъат угли Направление подготовки.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 42
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
n вершин, не могут быть одновременно вершины степени 0 и (n-1). Это значит, что из n вершин найдутся две, имеющие одинаковые степени.
Теорема 3.4. Если в графе с n вершинами (n больше или равно 2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.
Доказательство данной теоремы мы опускаем. Остановимся лишь на некотором ее пояснении. Содержание этой теоремы хорошо разъясняется задачей: группа, состоящая из n школьников, обменивается фотографиями. В некоторый момент времени выясняется, что двое совершили одинаковое число обменов. Доказать, что среди школьников есть либо один еще не начинавший обмена, либо один уже завершивший его.
Теорема 3.5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины.
Суть теоремы в том, что на этом графе невозможно найти цикл (как простой, так и непростой) нечетной длины, то есть содержащий нечетное число ребер.
Теорема 3.6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень.
Теорема 3.7. Для того, чтобы на связном графе можно было бы проложить цепь А В, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа.
Доказательство этой теоремы очень интересно и характерно для теории графов. Его также следует считать конструктивным (обратите внимание на то, как •использована при этом теорема 3.6). Для доказательства к исходному графу присоединяем ребро (А, В); после этого все вершины графа станут четными. Этот новый граф удовлетворяет всем условиям теоремы 3.6, и поэтому в нем можно проложить эйлеров цикл Ψ. И если теперь в этом цикле удалить ребро (А, В), то останется искомая цепь АВ.
На этом любопытном приеме основано доказательство следующей теоремы, которую следует считать обобщением теоремы 3.7.
Теорема 3.8. Если данный граф является связным и имеет 2kвершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному разу.
Теорема 3.9. Различных деревьев с n перенумерованными вершинами можно построитьnn-2.
По поводу доказательства этой теоремы сделаем одно замечание. Эта теорема известна, в основном, как вывод английского математика А. Кэли (1821-1895). Графы-деревья издавна привлекали внимание ученых. Сегодня двоичные деревья используются не только математиками, а и биологами, химиками, физиками и инженерами (подробнее об этом – в параграфе 6).
Теорема 3.10. Полный граф с пятью вершинами не является плоским.
Доказательство. Воспользуемся формулой Эйлера:
В- Р+ Г=2,
где В - число вершин плоского графа, Р - число его ребер, Г - число граней. Формула Эйлера справедлива для плоских связных графов, в которых ни один из многоугольников не лежит внутри другого. На рисунке 3.2, а изображен граф, к которому формула не применима – заштрихованный многоугольник находится внутри другого. Справа приведено изображение графа, к которому формула применима.
Эту формулу можно доказать методом математической индукции. Это доказательство мы опускаем. Заметим только, что формула справедлива и для пространственных многогранников. Пусть все пять вершин графа соединены друг с другом (рис. 3.2). Замечаем, что на графе нет ни одной грани, ограниченной только двумя ребрами. Если черезφ1обозначить число таких граней, тоφ2=0. Далее рассуждаем от противного, а именно: предположим, что исследуемый граф плоский. Это значит, что для него верна формула Эйлера. Число вершин в данном графе В=5, число ребер Р=10, тогда число граней Г=2-В+Р=2-5+10=7.
Это число можно представить в виде суммы:
Г=φ1+φ2+φ3+…,
гдеφ3-число граней, ограниченных тремя ребрами, φ4 - число граней, ограниченных четырьмя ребрами и т. д.
С другой стороны, каждое ребро является границей двух граней, а поэтому число граней равно 2Р, в то же время
2Р=20=3φ3+4φ4+....
Умножив равенство
Г=7=φ3+ φ4+ φ5+…
на три, получим
ЗГ=21=3(φ3+ φ4+ φ5+ …).
Ясно, что
(3φ3+3φ4+3φ5+…) < (3φ3+4φ4+5φ5+…)
или 3Г<2Р, но по условию, 2Р=20, а ЗГ=21; поэтому вывод, полученный при введенном нами предположении (граф плоский), противоречит условию. Отсюда заключаем, что полный граф с пятью вершинами не является плоским.
Теорема 3.11. (Теорема Понтрягина-Куратовского) Граф является плоским тогда и только тогда, когда он не имеет в качестве подграфа полного графа с пятью вершинами.
В заключение этого параграфа, на наш взгляд, следует упомянуть то, что в нем объяснялись только основные теоремы теории графов. Их практическое применение будет рассмотрено в следующих параграфах реферата.
Применение теории графов в школьном курсе математики
В соответствии с вышесказанным, в данном параграфе будут рассмотрены задачи, которые используются в школе на уроках математики.
Условно их можно классифицировать, подразделив на несколько групп:
1. Задачи о мостах.
2. Логические задачи.
3. Задачи о "правильном" раскрашивании карт.
4. Задачи на построение уникурсальных графов.
Рассмотрим несколько типичных примеров решения задач каждого вида.
Одной из наиболее известных задач о мостах является эйлерова задача; все остальные сформулированы похожим образом и решаются по тому же принципу. Поэтому в данном параграфе мы не будем подробно останавливаться разборе этого типа задач.
Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Это выявление логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов.
Задача 5.1. Из трех человек, стоящих рядом, один всегда говорит правду (правдолюб), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит либо правду, либо ложь (дипломат). У стоящего слева спросили: "Кто стоит рядом с тобой?". Он ответил: "Правдолюб". Стоящему в центре задали вопрос: "Кто ты?", и он ответил: "Я дипломат". Когда у стоящего справа спросили: "Кто стоит рядом с тобой?", он сказал: "Лжец". Кто где стоял?
Решение: Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности
Рассмотрим первую возможность. Если "правдолюб" стоит слева, то рядом с ним, судя по его ответу, также стоит "правдолюб". У нас же стоит "лжец". Следовательно, эта расстановка не удовлетворяет условию задачи. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что позиция "дипломат", "лжец", "правдолюб" удовлетворяет задаче. Действительно, если "правдолюб" стоит справа, то, по его ответу, рядом с ним стоит "лжец", что выполняется. Стоящий в центре заявляет, что он "дипломат", и, следовательно, лжет (что возможно из условия), а стоящий справа также лжет. Таким образом, все условия задачи выполнены.
Приложение теории графов в различных областях науки и техники
Графы и информация. Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Графы и химия. Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов, молекулы которых задаются формулой: CnH2n+2.
Все атомы углеводорода четырехвалентны, все атомы водорода одновалентны. Структурные формулы простейших углеводородов показаны на рисунке 6.1 (а – метанCH4, б – этанC2H6).
Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа.
Графы и биология. Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов – размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
Графы и физика. Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного параграфа.
Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.
В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:
1. Неориентированный граф:
· 1 – вершина инцидентна ребру;
· 0 – вершина не инцидентна ребру.
2. Ориентированный граф:
1 – вершина инцидентна ребру, и является его началом;
· 0 – вершина не инцидентна ребру;
· -1 – вершина инцидентна ребру, и является его концом.
Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа. Ребра обозначим буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.
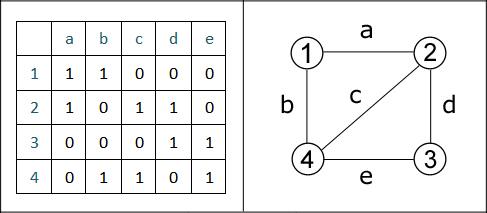
Рисунок 3.10 – Неориентированный граф и его матрица инцидентности
Для орграфа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в двух этих матрицах занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Дело в том, что в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина "1".
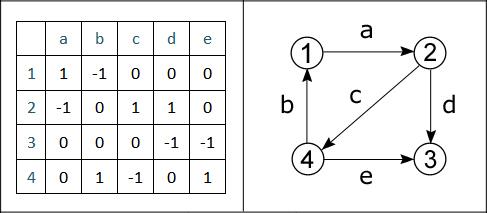
Рисунок 3.11 – Ориентированный граф и его матрица инцидентности
Теорема 3.4. Если в графе с n вершинами (n больше или равно 2) только одна пара имеет одинаковую степень, то в этом графе всегда найдется либо единственная изолированная вершина, либо единственная вершина, соединенная со всеми другими.
Доказательство данной теоремы мы опускаем. Остановимся лишь на некотором ее пояснении. Содержание этой теоремы хорошо разъясняется задачей: группа, состоящая из n школьников, обменивается фотографиями. В некоторый момент времени выясняется, что двое совершили одинаковое число обменов. Доказать, что среди школьников есть либо один еще не начинавший обмена, либо один уже завершивший его.
Теорема 3.5. Если у графа все простые циклы четной длины, то он не содержит ни одного цикла четной длины.
Суть теоремы в том, что на этом графе невозможно найти цикл (как простой, так и непростой) нечетной длины, то есть содержащий нечетное число ребер.
Теорема 3.6. Для того, чтобы граф был эйлеровым, необходимо и достаточно, чтобы он был связным и все его вершины имели четную степень.
Теорема 3.7. Для того, чтобы на связном графе можно было бы проложить цепь А В, содержащую все его ребра в точности по одному разу, необходимо и достаточно, чтобы А и В были единственными нечетными вершинами этого графа.
Доказательство этой теоремы очень интересно и характерно для теории графов. Его также следует считать конструктивным (обратите внимание на то, как •использована при этом теорема 3.6). Для доказательства к исходному графу присоединяем ребро (А, В); после этого все вершины графа станут четными. Этот новый граф удовлетворяет всем условиям теоремы 3.6, и поэтому в нем можно проложить эйлеров цикл Ψ. И если теперь в этом цикле удалить ребро (А, В), то останется искомая цепь АВ.
На этом любопытном приеме основано доказательство следующей теоремы, которую следует считать обобщением теоремы 3.7.
Теорема 3.8. Если данный граф является связным и имеет 2kвершин нечетной степени, то в нем можно провести k различных цепей, содержащих все его ребра в совокупности ровно по одному разу.
Теорема 3.9. Различных деревьев с n перенумерованными вершинами можно построитьnn-2.
По поводу доказательства этой теоремы сделаем одно замечание. Эта теорема известна, в основном, как вывод английского математика А. Кэли (1821-1895). Графы-деревья издавна привлекали внимание ученых. Сегодня двоичные деревья используются не только математиками, а и биологами, химиками, физиками и инженерами (подробнее об этом – в параграфе 6).
Теорема 3.10. Полный граф с пятью вершинами не является плоским.
Доказательство. Воспользуемся формулой Эйлера:
В- Р+ Г=2,
где В - число вершин плоского графа, Р - число его ребер, Г - число граней. Формула Эйлера справедлива для плоских связных графов, в которых ни один из многоугольников не лежит внутри другого. На рисунке 3.2, а изображен граф, к которому формула не применима – заштрихованный многоугольник находится внутри другого. Справа приведено изображение графа, к которому формула применима.
Эту формулу можно доказать методом математической индукции. Это доказательство мы опускаем. Заметим только, что формула справедлива и для пространственных многогранников. Пусть все пять вершин графа соединены друг с другом (рис. 3.2). Замечаем, что на графе нет ни одной грани, ограниченной только двумя ребрами. Если черезφ1обозначить число таких граней, тоφ2=0. Далее рассуждаем от противного, а именно: предположим, что исследуемый граф плоский. Это значит, что для него верна формула Эйлера. Число вершин в данном графе В=5, число ребер Р=10, тогда число граней Г=2-В+Р=2-5+10=7.
Это число можно представить в виде суммы:
Г=φ1+φ2+φ3+…,
гдеφ3-число граней, ограниченных тремя ребрами, φ4 - число граней, ограниченных четырьмя ребрами и т. д.
С другой стороны, каждое ребро является границей двух граней, а поэтому число граней равно 2Р, в то же время
2Р=20=3φ3+4φ4+....
Умножив равенство
Г=7=φ3+ φ4+ φ5+…
на три, получим
ЗГ=21=3(φ3+ φ4+ φ5+ …).
Ясно, что
(3φ3+3φ4+3φ5+…) < (3φ3+4φ4+5φ5+…)
или 3Г<2Р, но по условию, 2Р=20, а ЗГ=21; поэтому вывод, полученный при введенном нами предположении (граф плоский), противоречит условию. Отсюда заключаем, что полный граф с пятью вершинами не является плоским.
Теорема 3.11. (Теорема Понтрягина-Куратовского) Граф является плоским тогда и только тогда, когда он не имеет в качестве подграфа полного графа с пятью вершинами.
В заключение этого параграфа, на наш взгляд, следует упомянуть то, что в нем объяснялись только основные теоремы теории графов. Их практическое применение будет рассмотрено в следующих параграфах реферата.
Применение теории графов в школьном курсе математики
В соответствии с вышесказанным, в данном параграфе будут рассмотрены задачи, которые используются в школе на уроках математики.
Условно их можно классифицировать, подразделив на несколько групп:
1. Задачи о мостах.
2. Логические задачи.
3. Задачи о "правильном" раскрашивании карт.
4. Задачи на построение уникурсальных графов.
Рассмотрим несколько типичных примеров решения задач каждого вида.
Одной из наиболее известных задач о мостах является эйлерова задача; все остальные сформулированы похожим образом и решаются по тому же принципу. Поэтому в данном параграфе мы не будем подробно останавливаться разборе этого типа задач.
Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Это выявление логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов.
Задача 5.1. Из трех человек, стоящих рядом, один всегда говорит правду (правдолюб), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит либо правду, либо ложь (дипломат). У стоящего слева спросили: "Кто стоит рядом с тобой?". Он ответил: "Правдолюб". Стоящему в центре задали вопрос: "Кто ты?", и он ответил: "Я дипломат". Когда у стоящего справа спросили: "Кто стоит рядом с тобой?", он сказал: "Лжец". Кто где стоял?
Решение: Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности
Рассмотрим первую возможность. Если "правдолюб" стоит слева, то рядом с ним, судя по его ответу, также стоит "правдолюб". У нас же стоит "лжец". Следовательно, эта расстановка не удовлетворяет условию задачи. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что позиция "дипломат", "лжец", "правдолюб" удовлетворяет задаче. Действительно, если "правдолюб" стоит справа, то, по его ответу, рядом с ним стоит "лжец", что выполняется. Стоящий в центре заявляет, что он "дипломат", и, следовательно, лжет (что возможно из условия), а стоящий справа также лжет. Таким образом, все условия задачи выполнены.
Приложение теории графов в различных областях науки и техники
Графы и информация. Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Графы и химия. Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов, молекулы которых задаются формулой: CnH2n+2.
Все атомы углеводорода четырехвалентны, все атомы водорода одновалентны. Структурные формулы простейших углеводородов показаны на рисунке 6.1 (а – метанCH4, б – этанC2H6).
Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа.
Графы и биология. Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов – размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
Графы и физика. Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного параграфа.
Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.
В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:
1. Неориентированный граф:
· 1 – вершина инцидентна ребру;
· 0 – вершина не инцидентна ребру.
2. Ориентированный граф:
1 – вершина инцидентна ребру, и является его началом;
· 0 – вершина не инцидентна ребру;
· -1 – вершина инцидентна ребру, и является его концом.
Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа. Ребра обозначим буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.

Рисунок 3.10 – Неориентированный граф и его матрица инцидентности
Для орграфа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в двух этих матрицах занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Дело в том, что в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина "1".

Рисунок 3.11 – Ориентированный граф и его матрица инцидентности