МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ«Тюменский индустриальный университет»Институт геологии и нефтегазодобычиКафедра кибернетических системОсновы автоматизации технологических процессов нефтегазового производстваЛабораторная работа №3РАСЧЕТ УСТОЙЧИВОСТИ СИСТЕМАВТОМАТИЧЕСКОГО УПРАВЛЕНИЯВыполнил: студент группы ЭДНб-20-1Басиров Д.Д.Проверил: Смирнов В.И.Тюмень 2023Цель работы: изучение теоретических и практических положений в области автоматического контроля, регулирования и управления технологическими процессами нефтяной и газовой отрасли; формирование системного мышления в области автоматизации технологических процессов и производств.Задачи:

• 
  изучение общих принципов построения систем автоматизации;
  
• 
  ознакомление с классической теорией автоматического управления;
  
• 
  изучение и исследование технических средств автоматизации;
  
• 
  изучение методологических основ составления задания на автоматизацию производственного процесса.
  

Вариант – 4Дано:

Вариант	T0	Kпр	Kuy	Tuy	Kn	Tu
4	8	0,5	0,9	4	2	1

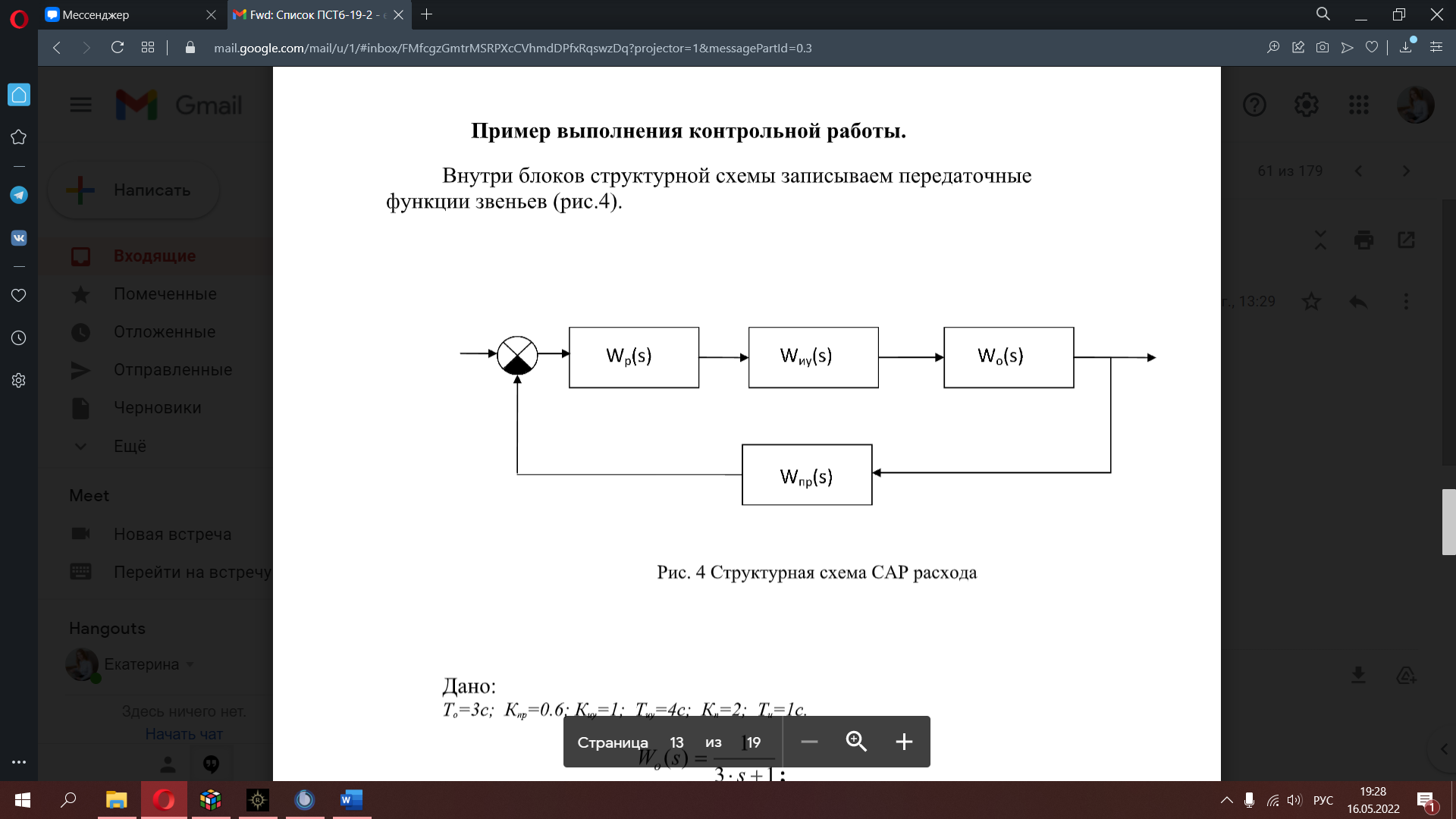
Ход работы:Рисунок 1 – Схема САР расхода

---

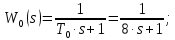
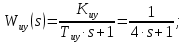
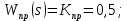
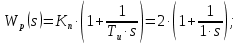
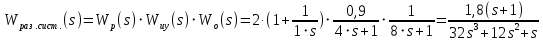
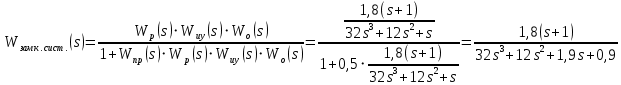
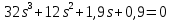
Находим передаточную функцию разомкнутой системы, состоящую из последовательно соединенных звеньев: регулятора расхода, исполнительного устройства и объекта управления.Находим передаточную функцию замкнутой системы:Знаменатель передаточной функции, замкнутой системы называется характеристическим уравнением (полиномом). 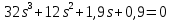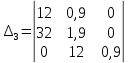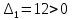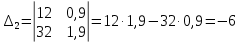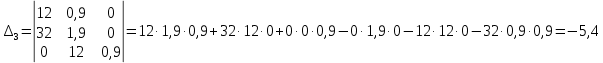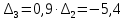Выписываем его, приравниваем к нулю и анализируем.Исследование устойчивости САР по критерию ГурвицаХарактеристическое уравнение (полином) замкнутой системы имеет вид:Составляем главный определитель ГурвицаОпределяем диагональные миноры этого определителя (по этому параметру система является устойчивой) (по данному параметру система является неустойчивой)илиПервый диагональный миноры главного определителя Гурвица оказался положительным, два остальных — отрицательные, следовательно, CAP будет неустойчива.Определение устойчивости САР по критерию МихайловаПостроить кривую-Михайлова и определить устойчивость системы автоматического регулирования, если характеристическое уравнение имеет вид: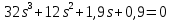Решение:Заменяем s на j , в результате чего получим: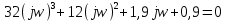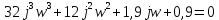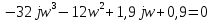Выделим в характеристическом уравнении на вещественную и мнимую части:

---

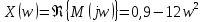
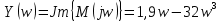
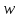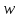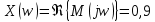
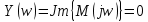
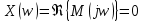
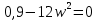
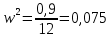
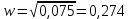
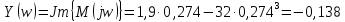
При = 0 получим первую точку годографа Михайлова. Заносим значение в таблицу и отмечаем координаты точки при = 0 на комплексной плоскости:Определяем вторую точку пересечения годографа с осями ко­ординат. Значение частоты , при которой характеристика пересекает мнимую ось, определяем, приравнивая вещественную часть к нулю:Находим значение мнимой части при этой частоте:Заносим полученные значения в таблицу при w = 0,274Находим третью точку пересечения кривой Михайлова с осями координат. 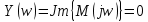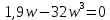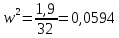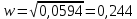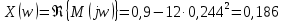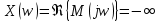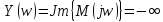Значение , при котором годограф пересекает вещес­твенную ось между третьим и вторым квадрантами, находим, при­равнивая мнимую часть к нулю:Находим значение вещественной части при этой частоте:Находим значения мнимой и вещественной частей при значении  =  :Результирующий угол поворота вектора при изменении  от 0 до 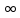равен 3п/2, (n=З) но при этом кривая Михайлова не проходит последовательно n - квадранты, где n - порядок дифференциального уравнения CAP, следствием этого является то, что то такая система будет

---

неустойчивой. Представленная система автоматического регулирования неустойчива по критерию Гурвица и по критерию Михайлова.Таблица 1

ω	0	0,1	0,2	0,244	0,274	0,3	0,4	0,5	0,6	∞
X(ω)	0,9	0,78	0,42	0,186	0	-0,18	-1,02	-2,1	-3,42	-∞
Y(ω)	0	0,158	0,124	0	-0,138	-0,294	-1,288	-3,05	-5,772	-∞

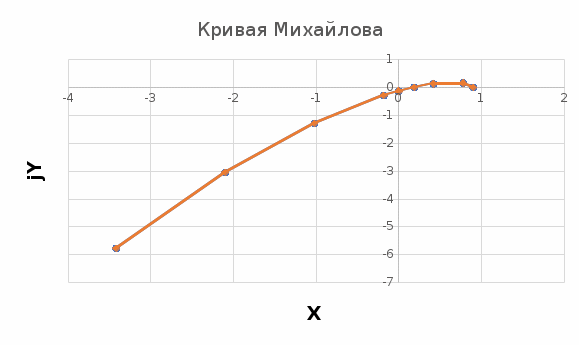
Рисунок 2 – Кривая МихайловаВывод: в ходе работы рассчитали устойчивость системы автоматического управления по критерию Гурвица, рассчитали устойчивость системы автоматического управления по критерию Михайлова, построили кривую Михайлова.

---

Смотрите также файлы

• Каждый студент проходящий производственную практику должен соблюдать инструктаж по технике безопасности.docx

• Из предложенного перечня выберите структуру альдегида Функциональная группа определяет химические свойства органических соединений.docx

• Учебник Биология,Оспанова. Алматы Атамра, 2018 Тема урока.docx

• Адатпаъ ылыми жмысты таырыбы рт сндіруші дрон растыру. Жмысты бірінші блімінде, дроны пайда болу жне даму тарихы, масаты мен міндеттері, пайдалану жолдары туралы айтылады..docx

• Пн информатика сынып 10 (жмб) іі тосан бойынша жиынты баалау тапсырмаларыны сипаттамасы.docx