Файл: 3mavzu Determinantning xossalari.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 102

Скачиваний: 19

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

3-mavzu

Determinantning xossalari

Reja

  1. Determinantning asosiy xossalari

  2. Minor va algebraic toldiruvchi tushunchalari

  3. Laplas teoremasi

6-xossa. Determinantda ikkita satr (ustun) oʻrinlari almashtirilsa, determinantning ishorasi oʻzgaradi. Masalan,



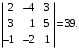
Endi bu matritsada birinchi va uchinchi ustunlarining oʻrinlarini almashtiramiz, u holda



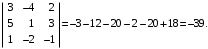
Bundan koʻrinib turibdiki, determinantlar faqat ishorasi bilan farq qiladi.

7-xossa. Agar determinant ikkita bir xil satr (ustun)ga ega boʻlsa, u holda uning qiymati nolga teng boʻladi. Masalan,



8-xossa. Agar determinantning biror satri (yoki ustuni) elementlariga boshqa satr (ustun)ning mos elementlarini biror songa koʻpaytirib qoʻshilsa, determinantning qiymati oʻzgarmaydi.



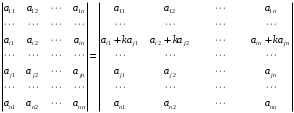
Masalan,



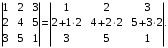
Haqiqatan ham, tenglikning chap tarafi



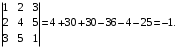
tenglikning oʻng tarafi:



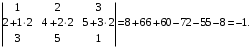
Demak tenglik oʻrinli.

9-xossa. Agar determinant ikki satri (ustuni)ning mos elementlari proporsional boʻlsa, u holda uning qiymati nolga teng boʻladi, ya’ni



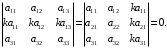
Masalan,



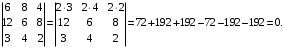
10-xossa. Transponirlash natijasida determinantning qiymati oʻzgarmaydi. Masalan,



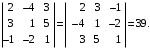
11-xossa. Agar determinant biror satri (ustuni)ning har bir elementi ikki qoʻshiluvchi yigʻindisidan iborat boʻlsa, u holda determinant ikki determinant yigʻindisiga teng boʻlib, ulardan birining tegishli satri (ustuni) birinchi qoʻshiluvchilaridan, ikkinchisining tegishli satri (ustuni) ikkinchi qoʻshiluvchilaridan iborat boʻladi, ya’ni:





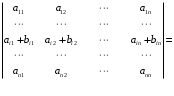
12-xossa. Agar determinant satr (ustun)laridan biri uning qolgan satr (ustun) larining chiziqli kombinatsiyasidan iborat boʻlsa, determinant nolga teng. Masalan,



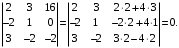
13-xossa. Toq tartibli har qanday qiya simmetrik matritsaning determinanti nolga teng. Masalan,



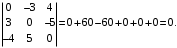
14-xossa. Bir xil tartibli ikkita matritsalar koʻpaytmasining determinanti, bu matritsalar determinantlarining koʻpaytmasiga teng, ya’ni:



Bizga 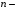tartibli kvadrat matritsa berilgan boʻlsin.

5-ta’rif. 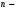tartibli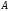
kvadrat matritsaning 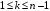tengsizlikni qanoatlantiruvchi ixtiyoriy 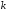ta satrlari va 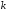ta ustunlari kesishgan joyda turgan elementlardan tashkil topgan 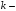tartibli matritsaning determinanti 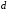determinantning 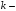tartibli minori deb ataladi.

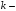tartibli minor sifatida kvadrat matritsaning 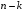ta satr va 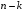ta ustunini oʻchirishdan hosil boʻlgan determinant, deb ham qarash mumkin.

6-ta’rif. Matritsaning diagonal elementlari yordamida hosil boʻlgan minorlar bosh minorlar deb ataladi.

7-ta’rif. tartibli kvadrat matritsada 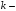tartibli 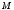minor turgan satrlar va ustunlar oʻchirib tashlangandan soʻng qolgan 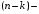tartibli 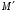minorga 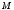minorning toʻldiruvchisi deyiladi va aksincha.

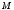minor va uning 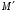toʻldiruvchi minorini sxematik ravishda quyidagicha tasvirlash mumkin:

.

Shunday qilib, determinantning oʻzaro toʻldiruvchi minorlar jufti haqida gapirish mumkin. Xususiy holda, 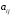element va determinantning 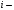satri va 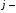ustunini oʻchirishdan hosil boʻlgan 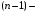tartibli minor oʻzaro toʻldiruvchi minorlar juftini hosil qiladi.

8-ta’rif. 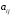elementning toʻldiruvchisi minori deb 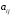element turgan satr va ustunni ochirishdan hosil boʻlgan determinantga aytiladi va 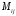deb belgilanadi.

9-ta’rif. 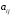minorning (elementning) algebraik toʻldiruvchisi deb
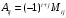songa aytiladi.

Laplas teoremasi. Determinantning qiymati uning ixtiyoriy satr (ustun) elementlari bilan, shu elementlarga mos algebraik toʻldiruvchilar koʻpaytmalari yigʻindisiga teng, ya’ni:



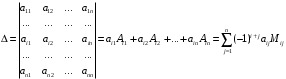
Bu formulaga 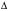determinantni 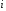satr elementlari boʻyicha yoyish formulasi deyiladi.

Determinantning biror satr (ustun) elementlari bilan uning boshqa satri (ustuni) elementlari algebraik toʻldiruvchilari koʻpaytmalarining yigʻindisi nolga teng.

4-misol. Quyidagi determinantni Laplas formulasi bilan hisoblang:



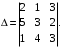
Yechish. Berilgan determinantni birinchi satr elementlari boʻyicha yoysak





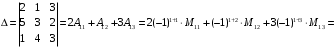
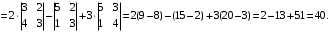
5-misol. Quyidagi determinantni Laplas formulasi bilan hisoblang:

.

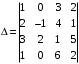Yechish. Berilgan determinantni ikkinchi ustun elementlari boʻyicha yoyib chiqamiz. Bu ustunda 2 ta noldan farqli element boʻlgani uchun natijada 2 ta 3-tartibli determinant hosil boʻladi.



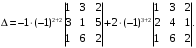
Yoki avval 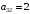elementni nolga keltirishimiz mumkin. Buning uchun 2-satrni 2 ga koʻpaytirib 3-satrga qoʻshamiz va hosil boʻlgan determinantni 2-ustun elementlariga nisbatan yoyamiz va hisoblaymiz: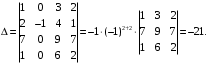



Koʻrinib turibdiki, Laplas teoremasidan yuqorida keltirilgan xossalar bilan birgalikda foydalanish determinantni hisoblashni ancha osonlashtiradi. Buning uchun biror satr yoki ustunni tanlab olib, shu ustun yoki satrdagi elementlarni determinantning xossalaridan foydalanib iloji boricha nollarga keltirishimiz kerak boʻladi. Soʻngra, Laplas teoremasi yordamida determinantning tartibini bittaga kamaytirishimiz mumkin.

6-misol. 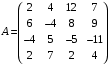matritsaning determinantini hisoblang.

Yechish. Bu determinantni hisoblash uchun avval 8-xossadan foydalanib, birinchi ustunining birinchi elementidan boshqa barcha elementlarini nolga aylantirib olamiz, keyin Laplas teoremasini qoʻllaymiz:



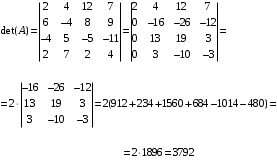
O‘z-o‘zini tekshirish uchun savollar

  1. Determinantda ikkita satr (ustun) oʻrinlari almashtirilsa, determinantning qiymati oʻzgaradimi?

  2. Agar determinant ikkita bir xil satr (ustun)ga ega boʻlsa, u holda uning qiymati nimaga teng boʻladi?

  3. Agar determinant ikki satri (ustuni)ning mos elementlari proporsional boʻlsa, u holda uning qiymati nimaga teng boʻladi?

  4. Transponirlash natijasida determinantning qiymati qanday oʻzgaradi.

  5. Agar determinant biror satri (ustuni)ning har bir elementi ikki qoʻshiluvchi yigʻindisidan iborat boʻlsa, u holda determinantni ikki determinant yigʻindisi korinishida yozish mumkinmi?

  6. Agar determinant satr (ustun)laridan biri uning qolgan satr (ustun) larining chiziqli kombinatsiyasidan iborat boʻlsa, determinant qiymati nimaga teng?

  7. Toq tartibli qiya simmetrik matritsaning determinant nimaga teng?

  8. n-tartibli determinant ixtiyoriy elementining minori deb nimaga aytiladi?

  9. Algebraik to’ldiruvchi yoki ad’yunkt deb nimaga aytiladi?

  10. Determinantni transponirlashdan tashqari uning ustida qanday almashtirishlar bajarganda kattaligi o’zgarmaydi?

  11. n-tartibli kvadrat matritsaning determinanti yoki aniqlovchisi deb nimaga aytiladi?

Asosiy adabiyotlar:

  1. Gilbert Strang “Introduction to Linear Algebra”, USA, Cambridge press,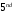 Edition, 2016.

  2. Grewal B.S. “Higher Engineering Mathematics”, Delhi, Khanna publishers,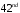 Edition, 2012.

  3. Raxmatov R.R., Adizov A.A., Tadjibayeva Sh.E., Shoimardonov S.K. Chiziqli algebra va analitik geometriya. O‘quv qollanma. Toshkent 2020.

  4. Rаxмаtоv R.R., Adizov A.A. “Chiziqli fazo va chiziqli operatorlar” O‘quv uslubiy qollanma. TATU, Toshkent 2019.

  5. Соатов Ё.У. “Олий математика”, Т., Ўқитувчи нашриёти, 1- 5 қисмлар, 1995.

  6. Рябушко А.П. и др. “Сборник индивидуальных заданий по высшей математике”, Минск, Высшая школа, 1-3 частях, 1991.

Asosiy adabiyotlar:

  1. Мирзиёев Ш. Буюк келажагимизни мард ва олижаноб халқимиз билан бирга қурамиз. –Т.: Ўзбекистон, 2017. - 488 бет.

  2. Мирзиёев Ш.М. Қонун устуворлиги ва инсон манфаатларини таъминлаш-юрт тараққиёти ва халқ фаровонлигининг гарови. –Т.: Ўзбекистон, 2017.

  3. Мирзиёев Ш.М. Эркин ва фаровон, демократик Ўзбекистон давлатини биргаликда барпо этамиз. Т.: Ўзбекистон, 2017.

  4. Adizov A.A., Xudoyberganov M.O‘. Amaliy matematika. O‘quv uslubiy qo‘llanma. Toshkent. 2014.

  5. Шодиев Т.Ш. Аналитик геометрия ва чизиқли алгебра. Тошкент “Ўқитувчи” 1984.

  6. Ильин В. А., Позняк Э. Г. Линейная алгебра. — 6-е изд., стер. — М.: ФИЗМАТЛИТ, 2004.

  7. Задорожный В. Н. и др. Высшая математика для технических

университетов. Часть I. Линейная алгебра. - Томск: Изд-во ТПУ, 2009.

  1. Данко П.С., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Седьмое издание. -М.: Высшая; школа, 2015.

  2. Семёнова Т.В. Высшая математика: учебное пособие для студентов технических вузов. Часть 1. - Пенза: Пензенский гос. ун-т, 2008.

  3. Макаров Е. В., Лунгу К. Н. Высшая математика: руководство к решению задач: учебное пособие, Часть 1, Физматлит. 2013.

  4. Минорский В.И. Сборник задач по высшей математике. М: Наука, 1987.

  5. Беклемешев Д.В., Петрович А.Ю., Чуберов И.А. Сборник задач по аналитической геометрии и линейной алгебре. -М.: Наука, 1987.

  6. Бугров Я.С., Николский С.М. Сборник задач по высшей математике, - М.: Наука. 1997.

Смотрите также файлы