МИНОБРНАУКИ РОССИИСанкт-Петербургский государственныйэлектротехнический университет«ЛЭТИ» им. В.И. Ульянова (Ленина)Кафедра Информационной безопасностиотчетпо лабораторной работе №1по дисциплине «Алгоритмы и структуры данных»Тема: Методы сортировки

Студент гр. 0361		Леонова М.А.
Преподаватель		Краснов С.А.

Санкт-Петербург2021

1. 
   Цель работы
   

Ознакомление с алгоритмами сортировки линейных и нелинейных структур и методикой оценки эффективности алгоритмов.

2. 
   Задание на лабораторную работу:
   

Выполнить сортировку массива из N чисел. Предусмотреть в программе учет времени сортировки для указанных значений 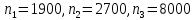. Составить программу, реализующую метод Хоара. Произвести расчет функции сложности разработанного алгоритма по полученным временным затратам. Провести анализ отклонения полученной в результате эксперимента сложности алгоритма от теоретической; построить графические зависимости времени сортировки от количества элементов сортируемого массива.

3. 
   Теоретические сведения
   

Метод Хоара – это алгоритм сортировки, который основан на разделении рассматриваемой части массива на две части таким образом, чтобы вес любого элемента одной части не превосходил веса любого элемента другой части. То есть в методе быстрой сортировки фиксируется какой-либо опорный элемент, относительно которого все элементы с большим весом перебрасываются вправо, а с меньшим – влево. При этом весь список элементов делится относительно опорного элемента на две части. Для каждой части процесс повторяется. Теоретически для опорного элемента следует выбирать медиану массива, однако на практике руководствуются лишь принципом постоянного выбора, то есть каждый раз при разбиении опорный элемент выбирается из одних и тех же соображений.

---

Алгоритм быстрой сортировки включает в себя два основных этапа:

• 
  разбиение массива относительно опорного элемента;
  
• 
  рекурсивная сортировка каждой части массива.
  

4. 
   Блок-схема алгоритма
   

Рисунок 4.1 – Блок-схема алгоритма

5. 
   Результаты выполнения программы
   

При запуске программы пользователю предлагается ввести количество элементов массива, которое должно быть целым и положительным. Демонстрация на рисунке 5.1.Рисунок 5.1 – Ввод количества элементов массиваПосле того, как пользователь введет число, оно появится в окне, а программа выведет на экран сгенерированный неупорядоченный массив из заданного количества элементов. Демонстрация на рисунке 5.2.Рисунок 5.2 – Вывод неупорядоченного массиваЗатем, используя метод Хоара, программа отсортирует заданный массив и выведет его на экран. Демонстрация на рисунке 5.3.Рисунок 5.3 – Вывод упорядоченного массиваВ конце программа выведет время, за которое была совершена сортировка (в секундах). Демонстрация на рисунке 5.4.Рисунок 5.4 – Вывод времени работы алгоритма

6. 
   Результаты выполнения работы
   

В таблице, приведенной ниже, представлены результаты выполнения работы. Из данной таблицы можно сделать вывод, что время сортировки растет с количеством элементов в массиве примерно как 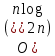.Таблица 6.1 – Результаты выполнения работы

Метод сортировки	Количество элементов	Время сортировки (сек)
Метод Хоара	1900	0,001
	2700	0,002
	8000	0,008

---

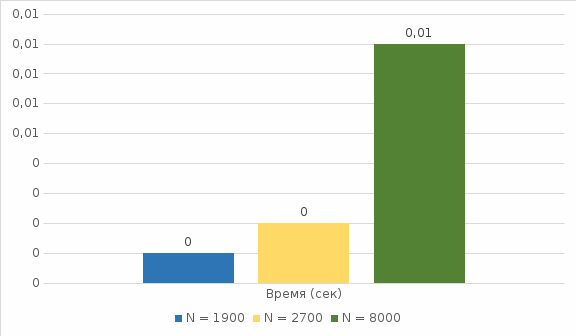
На приведенной ниже диаграмме представлена зависимость времени сортировки от количества элементов сортируемого массива.Рисунок 6.1 – Зависимость времени от количества элементовВ таблице, приведенной ниже, представлена сложность выполнения алгоритма, для лучшего, среднего и наихудшего случая.Таблица 6.2 – Сложность алгоритма

Лучший случай	Средний случай	Наихудший случай

7. 
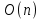   Выводы по работе
   

В ходе выполнения данной лабораторной работы:

• 
  были изучены методы сортировки;
  
• 
  написана программа, реализующая быструю сортировку, т.е. метод Хоара
  

Был предусмотрен учет времени сортировки для значений . По результатам запусков программы можно сделать вывод, что время сортировки растет с увеличением количества элементов в массиве примерно как 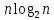. Соответственно, теоретическая сложность алгоритма совпадает с практической сложностью алгоритма. В ходе лабораторной работы была построена графическая зависимость времени сортировки от количества элементов в массиве. По итогам лабораторной работы №1 можно сделать вывод, что данный метод сортировки рекомендуется использовать в массивах с большим количеством элементов, так как он эффективен по времени.ПРИЛОЖЕНИЕ 1ИСХОДНЫЙ КОД ПРОГРАММЫФайл Метод Хоара.cpp#include

#include

#include

#include

#include
using namespace std;
void FillingTheMas(vector& mas)

{

for (size_t i = 0; i < mas.size(); i++)

{

mas[i] = static_cast(rand() % 100);

cout << mas[i] << " ";

}

cout << endl;

}
float Quicksort(vector& mas, int first, int last)

{

clock_t start = clock();
int mid = 0;

int f = first;

int l = last;
mid = mas[(f + l) / 2];

do

{

while (mas[f] < mid) f++;

while (mas[l] > mid) l--;

if (f <= l)

{

swap(mas[f], mas[l]);

f++;

l--;

}

} while (f < l);

if (first < l) Quicksort(mas, first, l);

if (f < last) Quicksort(mas, f, last);
return (float)(clock() - start) / CLOCKS_PER_SEC;

}
int main()

{

setlocale(LC_ALL, "Russian");

cout << "Леонова Мария, группа 0361, представляю программу, реализующую метод Хоара." << endl;

cout << "В конце программа выведет время, за которое была совершена сортировка (в секундах)." << endl;

cout << endl;
Sleep(3000);
int U;

cout << "Введите количество элементов массива (это должно быть положительное и целое число): ";
while (!(cin >> U) || U <= 0)

{

cin.clear();

cin.ignore(100, '\n');

cout << endl;

cout << "Ошибка! Попробуйте ввести заново: ";

}

cout << endl;

vector mas;
mas.reserve(U);
for (int i = 0; i < U; i++) mas.push_back(0);
srand(time(0));
cout << "Сортировка для массива из " << U << " элементов (неупорядоченный): " << endl;

cout << endl;
Sleep(4000);
FillingTheMas(mas);

cout << endl;
cout << "Сортировка для массива из " << U << " элементов (упорядоченный): " << endl;

cout << endl;
Sleep(4000);
float time = Quicksort(mas, 0, mas.size() - 1);
for (int i = 0; i < mas.size(); i++) cout << mas[i] << " ";

cout << endl;

cout << endl;
cout << "Время сортировки = " << time << " секунд" << endl;
Sleep(3000);
mas.clear();

cin.ignore();

}

---

Смотрите также файлы

• Баширова Райсат Кадиевна.pdf

• Что такое брови и какую роль они играют.odt

• Тарас Бульба характер, рожденный временем.docx

• 3mavzu Determinantning xossalari.docx

• Инструкция Прикрепите фитиля к банке с помощью наклейки. Растопите воск на водяной бане.docx