ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Математических и естественно-научных дисциплин
| Рейтинговая работа | Расчетно-аналитическое задание |
| по дисциплине | Теория вероятностей и математическая статистика |
| | |
| Задание / Вариант | № |
| | |
| | |
| Выполнена обучающимся группы | _______________________________ |
| ФИО обучающегося | _______________________________ |
| | |
| Преподаватель | _______________________________ |
Москва – 2023 г.
Оглавление
-
Вероятность……………………………………...……………… 3-4 -
Дисперсия случайной величины…………………………………5 -
Список использованной литературы…………………….………6
-
Вероятность
Задание 1. В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, и для третьей – 4%. Чему равна вероятность того, что оказавшееся нестандартным изделие произведено на ПЕРВОЙ фабрике?
Решение:
Наугад взятое изделие оказалось нестандартным (событие A), это связано с одним из трех событий: изделие изготовлено на первой фабрике (
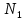); изделие изготовлено на второй фабрике (
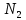) или изделие изготовлено на третей фабрике (
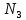). Объединение событий 
, 
и 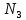дает полную группу вариантов. 
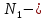продукция поступила с первой фабрики.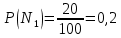
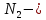продукция поступила с первой фабрики.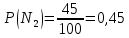
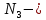продукция поступила с первой фабрики.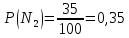
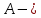изделие оказалось нестандартным.Условия вероятности этого события равны:
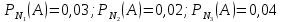
Далее обратимся к формуле полной вероятности.
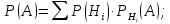
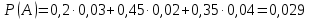
Наугад взятое изделие оказалось нестандартным, то есть событие A наступило. Для вычисления вероятность того, что изделие было произведено на первой фабрике, обратимся к формуле Байеса:
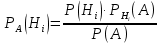
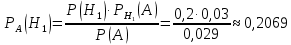
Ответ: вероятность того, что оказавшееся нестандартным изделие произведено на первой фабрике равно 0,2069.
-
Дисперсия случайной величины
Задание 2. Найти дисперсию случайной величины Х, имеющей следующий закон распределения
| Значение X | 1 | 2 | 3 | 4 | 5 |
| Вероятность | 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Решение:
Обратимся к формуле для определения математического ожидания:
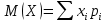
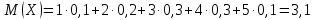
Далее обратимся к формуле дисперсии для дискретной случайной величины:
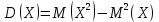
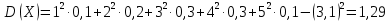
Ответ:
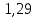
Список использованной литературы
-
Омельченко В.П., Карасенко Н.В., Математика [Электронный ресурс]. Издательство: НИЦ ИНФРА-М, 2022. – 349 с. https://znanium.com/catalog/document?pid=1855784 -
Балдин К. В., Башлыков В. Н., Рукосуев А. В. Теория вероятностей и математическая статистика Теория вероятностей Математическая статистика., Издательство: Дашков и К°, 2021, 472 с. -
Материал из Википедии — свободной энциклопедии https://ru.wikipedia.org/wiki/ -
Учебная статья Дисперсия случайной величины https://www.matematicus.ru/teoriya-veroyatnosti/dispersiya-sluchajnoj-velichiny -
Учебная статья Орел или решка? Основы теории вероятностей простыми словами https://proglib.io/p/orel-ili-reshka-osnovy-teorii-veroyatnostey-prostymi-slovami-2022-07