КОНТРОЛЬНАЯ РАБОТА
ЗАДАЧА 1

1 – 10.

1. 
   Подбрасываются две игральные кости. Требуется:
   

1) описать множество элементарных случайных событий,

2) найти вероятности событий А ={выпадение двух «шестерок»}, В = {выпадение хотя бы одной «шестерки»}, С = {выпадение одной «шестерки»}.

2. 
   В контейнере находятся 40 телевизоров, среди которых 5 имеют скрытые дефекты. Найти вероятность того, что 3 наудачу выбранных телевизора не будут иметь дефектов.
   
3. 
   Аудитор проверяет три счета. Вероятность правильного оформления счета равна 0,9. Найти вероятности событий А = {правильно оформлены три счета}, В = {правильно оформлены два счета}, С = {правильно оформлен один счет}, D = {правильно оформлен хотя бы один счет}.
   
4. 
   Инвестор наудачу приобретает акции двух фондов из 10. Среди 10 фондов 4 невыгодные. Найти вероятности событий А = {инвестор вкладывает деньги в выгодные фонды}, В = {инвестор вкладывает деньги в невыгодные фонды}, С ={инвестор вкладывает деньги хотя бы в один выгодный фонд}.
   
5. 
   В каждом из двух ящиков содержатся 6 черных и 4 белых шара. Из первого ящика наудачу переложили во второй ящик 1 шар. Найти вероятность того, что два наугад взятые шара из второго ящика будут белыми.
   
6. 
   На склад поступают однотипные детали с двух заводов – №1 и №2. Завод №1 поставляет 30% деталей, из которых 10% имеют низкое качество. Завод №2 производит детали, из которых 80% имеют высокое качество. Найти вероятность того, что наугад взятая со склада деталь будет высокого качества.
   
7. 
   Из трех урн наудачу извлекается один шар в соответствии с правилом: при подбрасывании игральной кости, если выпадает 1 очко, то выбирается урна 1; если выпадает 2, 3 или 4 очка, то выбирается урна 2; если выпадает 5 или 6 очков, то урна 3. В урне 1 находится 10 шаров, из них 2 красных, в урне 2 – 15 шаров, из них 3 красных, в урне 3 – 20 шаров, из них 10 красных. Найти вероятности событий А = {будет извлечен красный шар}, В = {извлеченный красный шар принадлежит урне 1}.
   
8. 
   В магазине представлена обувь трех фабрик: 30% обуви поставила фабрика 1, 25% – фабрика 2, остальную обувь – фабрика 3. Покупатель выбирает обувь наудачу. Процент возврата обуви, изготовленной фабрикой 1 – 3%, фабрикой 2 – 1%, фабрикой 3 – 0,5%. Найти вероятности событий А = {обувь покупателем не будет возвращена}, В = {невозвращенная обувь изготовлена фабрикой 3}.
   
9. 
   Автомат изготавливает однотипные детали, 5% произведенной продукции оказывается бракованной. Найти вероятность того, что из четырех последовательно изготовленных деталей будут бракованными не более двух.
   
10. 
    Вероятность поражения стрелком мишени при одном выстреле равна 0,8. Найти вероятность того, что при пяти последовательных выстрелах будет не менее четырех попаданий.
    

---

ЗАДАЧА 2

11 – 20. Задана функция плотности распределения вероятностей f(x) непрерывной случайной величины Х.

11.		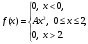a = 1, b = 1,7.
12.		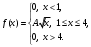a = 2, b = 3.
13.		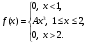a = 1,1, b = 1,5.
14.		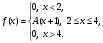a = 3, b = 3,5.
15.		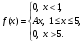a = 2, b = 3.
16.		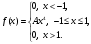a = 0,5, b = 1.

Требуется:

1. 
   найти коэффициент А;
   
2. 
   найти функцию распределения F(x);
   
3. 
   схематично построить графики F(x), f(x);
   
4. 
   найти математическое ожидание и дисперсию Х;
   
5. 
   найти вероятность того, что Х примет значение из интервала (a, b).
   

17 – 20. Задана функция распределения вероятностей F(x) непрерывной случайной величины Х.

17.		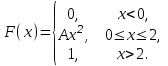a = 1, b = 2.
18.		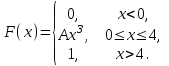a = 2, b = 3.
19.		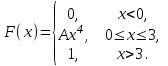a = 1, b = 2.
20.		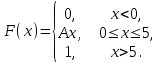a = 2, b = 4.

Требуется:

1. 
   найти функцию плотности распределения вероятностей f(x);
   
2. 
   найти коэффициент А;
   
3. 
   схематично построить графики F(x), f(x);
   
4. 
   найти математическое ожидание и дисперсию Х;
   
5. 
   найти вероятность того, что Х примет значение из интервала (a, b).
   

ЗАДАЧА 3

21 – 30. Заданы математическое ожидание aи среднее квадратическое отклонение

---

σ нормально распределенной случайной величины Х.

21.	a = 1, σ = 5, α = 0,5, β = 3.	22.	a = 9, σ = 5, α = 2, β = 8.
23.	a = 2, σ = 4, α = 1, β = 5.	24.	a = 8, σ = 3, α = 1, β = 6.
25.	a = 3, σ = 2, α = 2, β = 8.	26.	a = 6, σ = 4, α = 0, β = 5.
27.	a = 4, σ = 4, α = 3, β = 6.	28.	a = 4, σ = 6,α = 5, β = 9.
29.	a = 5, σ = 6, α = 4, β = 9.	30.	a = 2, σ = 3, α = 4, β = 8.

Требуется:

1. 
   написать функцию плотности распределения вероятностей f(x) и схематично построить ее график;
   
2. 
   найти вероятность того, что Х примет значение из интервала (a, b).
   

ЗАДАЧА 4

31 – 40. Производится некоторый опыт, в котором случайное событие А может появиться с вероятностью p. Опыт повторяют в неизменных условиях n раз.

31. n = 900; p = 0,3 . Определить вероятность того, что в 900 опытах событие А произойдет от 250 до 320 раз.

32. n = 800; p = 0,4 . Определить вероятность того, что относительная частота появления события А отклонится от p = 0,4 не более, чем на 0,05.

33. n = 1000; p = 0,6 . Определить вероятность того, что в 1000 опытах событие А произойдет не менее чем 580 раз.

34. n = 700; p = 0,45 . Определить вероятность того, что в 700 опытах событие А произойдет в меньшинстве опытов.

35. n = 900; p = 0,5 . Определить вероятность того, что в 900 опытах событие А произойдет в большинстве опытов.

36. n = 800; p = 0,6 . Определить вероятность того, что в 800 опытах относительная частота появления события А отклонится от вероятности p = 0,6 не более, чем на 0,05.

37. n = 1000; p = 0,4 . Найти, какое отклонение относительной частоты появления события А от p = 0,4 можно ожидать с вероятностью 0,9.

38. p = 0,6 . Определить сколько раз (n) надо провести опыт, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события А от

---

p = 0,6 не более, чем 0,05.

39. n = 900; p = 0,8 . Найти вероятность того, что относительная частота появления события А отклонится от p = 0,8 не более, чем на 0,1.

40. n = 800; p = 0,4 . Определить вероятность того, что в 800 опытах событие А произойдет от 300 до 400 раз.

ЗАДАЧА 5

41 – 50. В результате 10 независимых измерений некоторой величины Х, выполненных с одинаковой точностью, получены опытные данные, приведенные в таблице. Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины Хпри помощи доверительного интервала, покрывающего истинное значение величины Хс доверительной вероятностью 0,95.
_{Исходныеданные}

№ задачи	х1	х2	х3	х4	х5	х6	х7	х8	х9	х10
41. 42. 43. 44. 45. 46. 47. 48. 49. 50.	1,2 3,7 5,3 6,3 7,1 7,9 6,3 6,9 8,7 3,1	2,3 4,2 3,7 6,8 6,3 7,7 8,2 7,3 8,9 5,2	2,7 4,4 6,2 4,9 6,2 8,7 8,4 7,1 6,9 3,9	2,1 5,3 3,9 5,5 5,8 8,1 9,1 9,5 9,4 4,4	2,6 3,5 4,4 5,3 7,7 6,3 8,6 9,7 9,3 5,3	3,1 4,0 4,9 5,2 6,8 9,0 8,3 7,9 8,5 5,9	1,8 3,3 5,0 6,1 6,7 7,8 8,9 7,6 9,2 4,2	3,0 3,8 4,1 6,6 5,9 8,3 8,0 9,1 9,9 4,6	1,7 4,1 3,8 6,0 5,7 8,6 9,6 6,6 8,6 4,8	1,4 5,2 4,2 5,7 5,1 8,4 7,9 9,9 6,4 3,9

---

ЗАДАЧА 6

51 – 60. Отдел технического контроля проверил n партий однотипных изделий и установил, что число Х нестандартных изделий в одной партии имеет эмпирическое распределение, приведенное в таблице, в одной строке которой указано количество x_i нестандартных изделий в одной партии, а в другой строке – количество n_i партий, содержащих x_i нестандартных изделий. Требуется при уровне значимости α = 0,05 проверить гипотезу о том, что случайная величина Х (число нестандартных изделий в одной партии) распределена по закону Пуассона.
_{Исходныеданные}

№ задания	n= ∑ ni	xi	0	1	2	3	4	5
51. 52. 53. 54. 55. 56. 57. 58. 59. 60.	1000 500 1000 500 1000 400 1000 500 1000 500	ni ni ni ni ni ni ni ni ni	370 70 380 220 403 185 155 194 440 201	360 140 380 180 370 180 265 186 365 184	190 135 170 75 167 13 266 88 145 85	63 95 58 20 46 13 194 26 41 22	14 40 10 4 12 7 83 5 8 7	3 20 2 1 2 2 37 1 1 1

---

Смотрите также файлы

• Государственное бюджетное профессиональное образовательное учреждение Пермский колледж транспорта и сервиса.docx

• Дополнительные типы данных в python множества, кортежи, словари.pptx

• "Технология виртуальных частных сетей vpn ".doc

• Контрольные вопросы для самостоятельной подготовки к семинарскому занятию 1 Вопросы Социальная динамика или концепция общественного прогресса О. Конта. Ответ Социальная динамика это теория прогресса, который О. Конт понимает как развитие порядка.docx

• Учебное пособие Пермь 2017.pdf