ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 59
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема: Истечение жидкости через отверстия и насадки
Лекция 7
7.1. Истечение жидкости через насадки.
Н
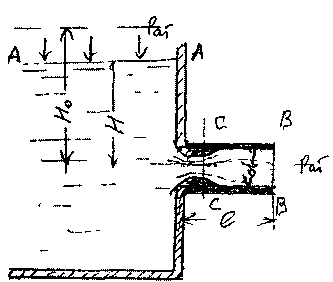 асадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадка полностью соответствовал размеру отверстия в тонкой стенке.
асадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадка полностью соответствовал размеру отверстия в тонкой стенке.Насадком называется короткая труба длиной обычно от 3 до 6 d, улучшающая условия вытекания жидкости. Например, если вода вытекает из бака через отверстие и насадок (рис. 15), которые расположены на одной и той же глубине и диаметры которых равны, то в насадке расход воды будет примерно на 30 % больше, чем в отверстии. Наличие такой направляющей трубки приведет к увеличению расхода жидкости при прочих равных условиях. Причины увеличения следующие. При отрыве струи от острой кромки отверстия струя попадает в канал насадка, а поскольку струя испытывает сжатие, то стенок насадка она касается на расстоянии от 1,0 до 1,5 его диаметра. Воздух, который первоначально находится в передней части насадка, вследствие неполного заполнения его жидкостью постепенно выносится вместе с потоком жидкости. Таким образом, в этой области образуется «мёртвая зона», давление в которой ниже, чем давление в окружающей среде (при истечении в атмосферу в «мёртвой зоне» образуется вакуум). За счёт этих факторов увеличивается перепад давления между резервуаром и областью за внешней его стенкой и в насадке генерируется так называемый эффект подсасывания жидкости из резервуара.
Однако наличие самого насадка увеличивает гидравлическое сопротивление для струи жидкости, т.к. в самом насадке появляются потери напора по длине трубки. Если трубка имеет ограниченную длину, то влияние подсасывающего эффекта с лихвой компенсирует дополнительные потери напора по длине. Практически эти эффекты (подсасывание и дополнительные сопротивления по длине) компенсируются при соотношении: / = 55 d. По этой причине длина насадков ограничивается / = (3 -5)d . По месту расположения насадки принято делить на внешние и внутренние насадки. Когда насадок монтируется с внешней стороны резервуара (внешний насадок), то он оказывается более технологичным, что придаёт ему преимущество перед внутренними насадками. По форме исполнения насадки подразделяются на цилиндрические и конические, а по форме входа в насадок выделяют ещё коноидальные насадки, вход жидкости в которые выполнен по форме струи.
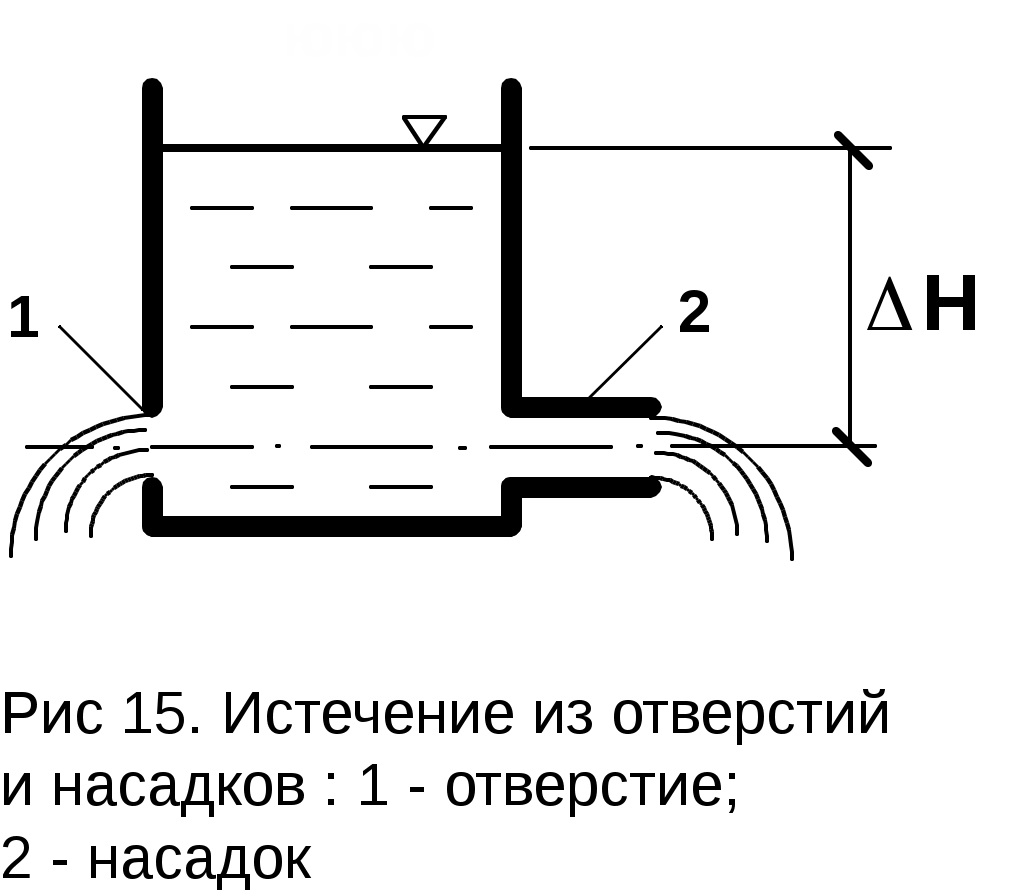
Простейшим насадком является цилиндрический насадок. Течение в нём может происходить в двух разных режимах. В первом случае на острых входных кромках насадка происходит совершенное сжатие струи и далее она движется, не касаясь стенок насадка. В этом случае истечение ничем не отличается от истечения через малое отверстие в тонкой стенке. Скорость при этом истечении высокая, а расход минимален.
Во втором случае, как и при истечении через отверстие в тонкой стенке, струя жидкости вначале сжимается на некотором удалении от входного сечения, образуя вихревую зону, давление в этом сечении струи становится меньше атмосферного. Далее струя постепенно расширяется и заполняет всё сечение насадка. Из-за того, что сжатия на выходе насадка нет (ε = 1,0) а коэффициент расхода через такой насадок равняется
При этом расход жидкости через насадок при прочих равных условиях превышает расход в первом случае, а скорость жидкости становится меньше из-за более высокого сопротивления.
Е

щё лучшие условия истечения наблюдаются при движении жидкости через так называемый тороидальный насадок, который обеспечивает более высокий коэффициент расхода. Его значение, в зависимости от увеличения радиуса скругления кромки, доходит до

.
Когда радиус кривизны становится больше длины насадка, насадок становится коноидальным. Коэффициент расхода в таких условиях истечения приближается к значению
Сходящиеся насадки. Если придать насадку форму конуса, сходящемуся по направлению к его выходному отверстию, то такой насадок будет относиться к группе сходящихся конических насадков. Такие насадки характеризуются углом конусности а. От величины этого угла зависят все характеристики насадков. Как коэффициент скорости, так и коэффициент расхода увеличиваются с увеличением угла конусности, при угле
»
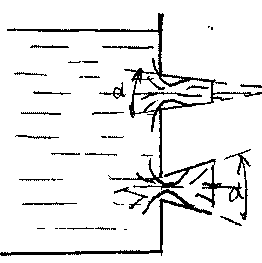 конусности в 13° достигается максимальное значение ко-
конусности в 13° достигается максимальное значение ко-эффициента расхода превышающее 0,94. При дальнейшем увеличении угла конусности насадок начинает работать как отверстие в тонкой стенке, при этом коэффициент скорости продолжает увеличиваться, а коэффициент расхода начинает убывать. Это объясняется тем, что уменьшаются потери на расширение струи после её сжатия. Область применения сходящихся насадков связана с теми случаями, когда необходимостью иметь большую выходную скорость струи жидкости при значительном напоре (сопла турбин, гидромониторы, брандспойты).
Расходящиеся насадки. Вакуум в сжатом сечении расходящихся насадков больше, чем у цилиндрических насадков и увеличивается с возрастанием угла конусности, что увеличивает расход жидкости. Но с увеличением угла конусности расходящихся насадков возрастает опасность отрыва струи от стенок насадков. Необходимо отметить, что потери энергии в расходящемся насадке больше, чем в насадках других типов. Область применения расходящихся насадков охватывает те случаи, где требуется большая пропускная способность при малых выходных скоростях жидкости (водоструйные насосы, эжекторы, гидроэлеваторы и др.)
К
 оноидальные насадки. В коноидальных насадках вход в насадки выполнен по профилю входящей струи. Это обеспечивает уменьшение потерь напора до минимума. Так значение коэффициентов скорости и расхода в коноидальных цилиндрических насадков достигает 0,97 - 0,99. 7.4. Истечение жидкости через широкое отверстие в боковой стенке. Истечение жидкости через большое отверстие в боковой стенке сосуда отличается от истечения через малое отверстие тем, что величина напора будет различной для различных площадок в сечении отверстия. Максимальным напором будет напор в площадках примыкающих к нижней кромке отверстия. В связи с этим и скорости в различных элементарных струйках проходящих через сечение отверстия также будут неодинаковы В то же время давление во внешней среде, в которую происходит истечение жидкости одинаково и равно атмосферному давлению.
оноидальные насадки. В коноидальных насадках вход в насадки выполнен по профилю входящей струи. Это обеспечивает уменьшение потерь напора до минимума. Так значение коэффициентов скорости и расхода в коноидальных цилиндрических насадков достигает 0,97 - 0,99. 7.4. Истечение жидкости через широкое отверстие в боковой стенке. Истечение жидкости через большое отверстие в боковой стенке сосуда отличается от истечения через малое отверстие тем, что величина напора будет различной для различных площадок в сечении отверстия. Максимальным напором будет напор в площадках примыкающих к нижней кромке отверстия. В связи с этим и скорости в различных элементарных струйках проходящих через сечение отверстия также будут неодинаковы В то же время давление во внешней среде, в которую происходит истечение жидкости одинаково и равно атмосферному давлению.7.2. Истечение жидкости из отверстий
Истечение жидкости из отверстий и насадков (коротких трубок различной формы и сечений) характерно тем, что в этом процессе потенциальная энергия жидкости на очень коротком расстоянии и за очень короткое время превращается в кинетическую энергию струи (или капель в общем случае). При этом происходят какие-то, большие или не очень, потери напора. Подобные режимы течения жидкости возникают при вытекании жидкости из резервуаров, баков, котлов в атмосферу или пространство, заполненное жидкостью. Аналогичные явления происходят при протекании жидкости через малые отверстия и щели в направляющей, контрольной и регулирующей аппаратуре различных гидравлических систем.
Основной вопрос, на который нужно найти ответ, состоит в том, как определить расход и скорость истечения через отверстия или насадки различной формы.
7.3. Сжатие струи
П
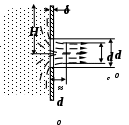 ри вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдается совершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия
ри вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдается совершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия  ,
,В том случае, если истечение происходит из резервуара такой формы, что его стенки влияют на траекторию движения частиц при входе в отверстие, наблюдается несовершенное сжатие струи.
В
 следствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия
следствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия
 ;
;где
 ;
;где, в свою очередь,
7.3. Истечение через малое отверстие в тонкой стенке
Рассмотрим большой резервуар с жидкостью, из которого через малое отверстие в боковой стенке вытекает струйка. Термины «большой резервуар» и «малое отверстие» означает, что эти размеры не сказываются на изменении высоты жидкости (напора) в резервуаре при вытекании из него жидкости. Термин «тонкая стенка» означает, что после сжатия струя вытекающей жидкости не касается цилиндрической поверхности отверстия.
Рассмотрим два сечения в этом резервуаре, обозначенные индексами 0 и С. Запишем уравнение Бернулли для этих условий:
 .
.Д
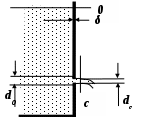 ля описанных условий можно считать, что движения жидкости в сечении 0 нет, следовательно, скоростной напор равен нулю. Разницей нивелирных высот, из-за их малого влияния можно пренебречь. Коэффициентом
ля описанных условий можно считать, что движения жидкости в сечении 0 нет, следовательно, скоростной напор равен нулю. Разницей нивелирных высот, из-за их малого влияния можно пренебречь. Коэффициентом  .
.После перегруппировки членов получим