Файл: Методические рекомендации по выполнению работы, линейка, карандаш. Указание.docx
Добавлен: 23.11.2023
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Основы электростатики. Теорема Гаусса
Цели работы: закрепить умения и навыки решения задач с использованием основного закона электростатики.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы, линейка, карандаш.
Указание: Практическая работа состоит из двух частей – теоритической и практической.
После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из двух и более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.
На выполнение практической работы отводится два академических часа.
1. Ознакомьтесь и повторите теоритические сведения, изученные на лекциях
а так же материал, размещённый в ЭОС по ссылкам:
https://edu.stankin.ru/mod/resource/view.php?id=301748
https://edu.stankin.ru/mod/resource/view.php?id=301864
https://edu.stankin.ru/mod/resource/view.php?id=301867
1. Теория. Основные понятия и формулы
3.1 Электростатика
По закону Кулона сила электростатического взаимодействия между двумя заряженными телами, размеры которых малы по сравнению с расстоянием r между ними, определяется формулой
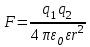
,где q1 и q2 – электрические заряды тел,
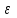- относительная диэлектрическая проницаемость среды, 
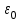= 8, 85 
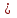10 -12 Ф/м – электрическая постоянная.Напряженность электрического поля определяется формулой
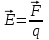,Где F – сила, действующая на заряд q.
Напряженность поля точечного заряда
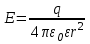
Напряженность электрического поля нескольких зарядов (например, поле диполя) находится по правилу векторного сложения.
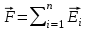
По теореме Гаусса поток напряженности сквозь любую замкнутую поверхность
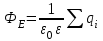,где
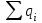- алгебраическая сумма зарядов, находящихся внутри этой поверхности.При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами:
А) напряженность поля, образованного бесконечно длинной нитью
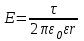,где τ – линейная плотность заряда на нити, r – расстояние от нити.
Если нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити на расстоянии r от неё
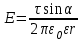,где α - угол между направлением нормали к нити и радиус-вектором, проведенным из рассматриваемой точки к концу нити.
Б) напряженность поля, образованного заряженной бесконечно длинной плоскостью
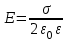,где
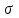- поверхностная плотность заряда на плоскости.В) напряженность поля, образованного разноименно заряженными параллельными бесконечными плоскостями (поле плоского конденсатора)
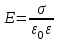.Г) напряженность поля, образованного заряженным шаром
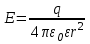
где q- заряд шара радиусом R, г – расстояние от центра шара до точки.
Разность потенциалов между двумя точками электрического поля определяется работой, которую надо совершить, чтобы единичный положительный заряд перенести из одной точки в другую:
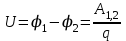.Потенциал поля точечного заряда
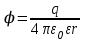,где r – расстояние от заряда.
Напряженность электрического поля и потенциал связаны соотношением
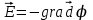
В случае однородного поля плоского конденсатора напряженность
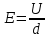,где U – разность потенциалов между пластинами конденсатора, d – расстояние между ними.
Потенциал уединенного проводника и его заряд связаны соотношением
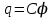,где С – емкость уединенного проводника.
Емкость плоского конденсатора
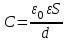,где S – площадь каждой пластины конденсатора.
Емкость сферического конденсатора
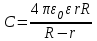,где r и R – радиусы внутренней и внешней сферы.
В частном случае, когда R = ∞,
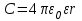
- емкость уединенного шара.
Емкость цилиндрического конденсатора
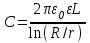,где L – высота коаксиальных цилиндров, r и R – радиусы внутреннего и внешнего цилиндров.
Емкость системы конденсаторов:
- при параллельном соединении конденсаторов
C = С1 + С2 + С3 + …
- при последовательном соединении
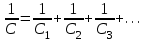
Энергия заряженного конденсатора может быть найдена по одной из следующих формул:
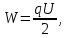
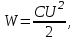
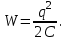
В случае плоского конденсатора энергия
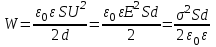,где S – площадь каждой пластины конденсатора,
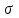- поверхностная плотность заряда на пластинах, U – разность потенциалов между пластинами, d – расстояние между ними.Объемная плотность энергии электростатического поля:
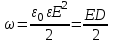,где D – электрическое смещение (D =
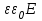).Сила притяжения между пластинами плоского конденсатора:
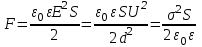.2 Примеры решения задач
Задача на теорему Гаусса №1: напряженность поля плоскости
Условие
Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.
Решение
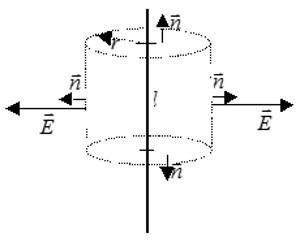
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:
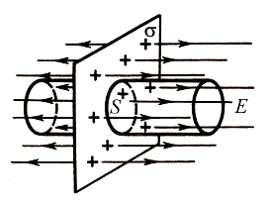
По теореме Гаусса:
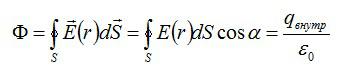
Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:
Согласно теореме Гаусса:
Отсюда:
Ответ:
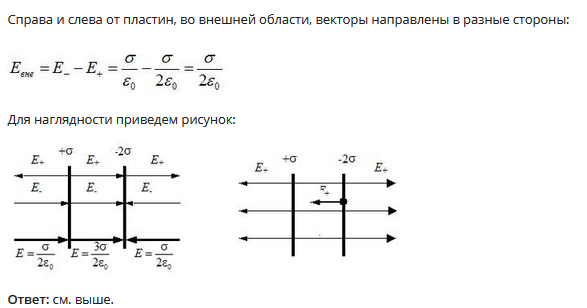
Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити
Условие
Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.
-
Ознакомьтесь с разбором и ходом решения задач. Решите подобную задачу для своего варианта.
Пример 1. Точечный заряд q = 25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R = 1 см, равномерно заряженным с поверхностной плотностью δ = 0,2 нКл/см2. Определить силу F, действующую на заряд, если его расстояние от оси цилиндра r = 10 см.
Р е ш е н и е. Значение силы F, действующей на точечный заряд q, находящийся в электрическом поле, определяется по формуле
F =qЕ, (1)
где Е - напряженность поля.
Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра
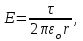(2)где τ – линейная плотность заряда.
Выразим линейную платность τ через поверхностную плотность δ. Для этого выделим элемент цилиндра длиной l и выразим находящийся на нем заряд q двумя способами: q = δS = δ2πRl. Приравняв правые части этих формул и сократив полученное равенство на l, найдем τ = 2πRδ. С учетом этого (2) примет вид Е=Rδ/(εо r). Подставив выражение Е в (1), получим F = qδR/εо r.
Произведем вычисления:
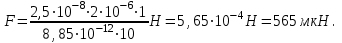
Сила F сонаправлена с напряженностью Е, которая в силу симметрии (цилиндр бесконечно длинный) перпендикулярна поверхности цилиндра.
Таблица 1 – Варианты заданий для решения Пример№1
| Вариант | q = нКл | R = 1 см | δ = нКл/см2 | r = 10 см. |
| 1 | 20 | = | 0,25 | = |
| 2 | 30 | = | 0,4 | = |
| 3 | 30 | = | 0,2 | = |
| 4 | 22 | = | 0,22 | = |
| 5 | 20 | = | 0,24 | = |
| 6 | 25 | = | 0,2 | = |
| 7 | 20 | = | 0,4 | = |
| 8 | 20 | = | 0,25 | = |
| 9 | 30 | = | 0,4 | = |
| 10 | 30 | = | 0,2 | = |
| 11 | 22 | = | 0,22 | = |
| 12 | 20 | = | 0,24 | = |
| 13 | 25 | = | 0,2 | = |
| 14 | 20 | = | 0,4 | = |
Пример 2. По тонкому кольцу размещён равномерно заряд q =40 нКл с линейной плотностью τ = 50нКл/м. Определить напряженность Е электрического поля, создаваемого этим зарядом в точке А, лежащей да оси кольца и удаленной от его центра на расстояние, равное половине радиуса.
Р е ш е н и е. Совместим координатную. плоскость х0у с плоскостью кольца, а ось 0z - с осью кольца (рис. 4).
Н
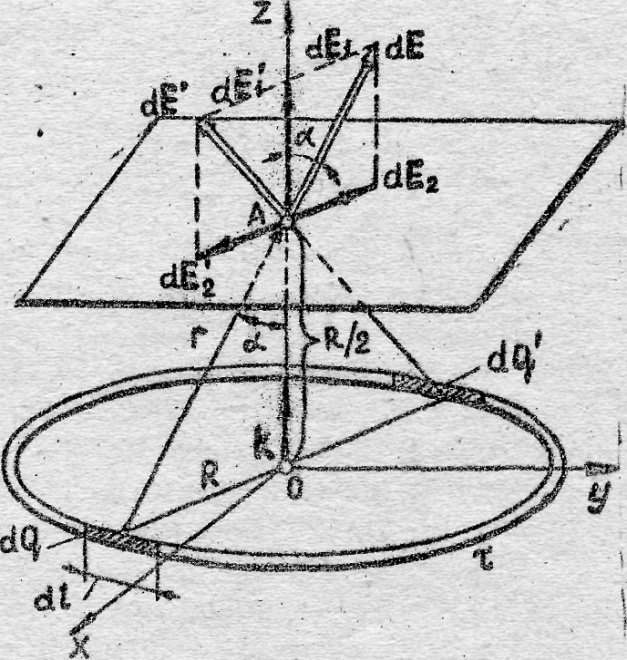а кольце выделим малый участок длиной dl. Так как заряд dq = τdl, находящейся на этом участке, можно считать точечным, то напряженность dE электрического поля, создаваемого этим зарядом, может быть записана в виде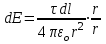 
где к - радиус-вектор, направленный от элемента dl к т. А.
Рис. 4
Разложим вектор dE на две составляющие: dЕ1 , перпендикулярную плоскости кольца (сонаправленную с осью 0z), и Е2 , параллельную плоскости кольца (плоскости х0у), т.е. dE = dE1 + dE2.
Напряженность электрического поля в т. А найдем интегрированием.
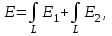
где интегрирование ведется по всем элементам заряженного кольца. Заметим, что для каждой пары зарядов dq и dq’(dq = dq’), расположенных симметрично относительно центра кольца, векторы dE2 и dE2’ в точке А равны по и противоположны по направлений: dE2= - dE2’. Поэтому векторная (интеграл)
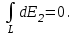Составляющие dE1 для всех элементов кольца сонаправлены с осью 0z (единичным вектором k), т. е, dE = kdE1. Тогда Е =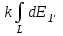
Так как
, 
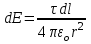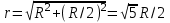и 
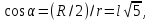то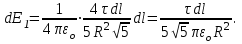
Таким образом,
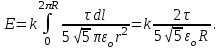
Из соотношения q=2πRτ определим радиус кольца: R = q/ (2πτ). Тогда
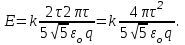
Модуль напряженности |E| = 4 πτ2 /
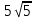εо q.Проворим, дает ли правая часть полученного равенства единицу напряженности (В/м):