Файл: Содержание введение 3 глава основы теории и вопросы моделирования.docx
Добавлен: 23.11.2023
Просмотров: 165
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.3. Диполь
Электрическое поле, образующееся системами из нескольких положительных и отрицательных зарядов, имеет определённые специфические особенности. Простейшая из таких систем - электрический диполь - два равных по величине и противоположных по знаку электрических заряда, расположенные на некотором расстоянии друг от друга, называемом плечом диполя.
Диполь в буквальном переводе с греческого языка означает двухполюсник, то есть система, состоящая из двух полюсов. Определение самого термина «диполь» безотносительно к тому, каким он является, не нашел.
Слово полюс (на латыни polus, от греческого pоlos) буквально означает ось, но это ничего не поясняет. Наиболее абстрактно звучит определение полюса в БСЭ: это «нечто диаметрально противоположное другому». Такому определению соответствуют положительный и отрицательный заряды в электромагнетизме, если считать, что имеется в виду противоположность по знаку. Учитывая это, диполь можно считать не столько двухполюсником, сколько двухзарядником, и определить диполь как физическую систему, состоящую из двух пространственно разделенных зарядов одной природы, но противоположного знака.
Многие атомы и молекулы представляют собой электрические диполи. Например, молекула. У неё избыток отрицательного заряда около кислородного атома и положительного около водородных атомов. Молекула, в которой центры отрицательного и положительного заряда ядер не совпадают, является электрическим диполем
Электрический диполь – это совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Впрочем, речь идет не столько о точечных статических зарядах (терминология зарядов поясняется отдельно), сколько о заряженных системах, центры которых отстоят друг от друга на расстоянии, названном дипольным расстоянием и обозначенным символом d. Каждый из двух зарядов называют монополем. Обозначение d выбрано потому, что при повороте диполя во-
круг своего центра дипольное расстояние становится диаметром окружности, по которой движутся монополи. В статье, посвященной повороту диполя, пока- зано, почему дипольное расстояние нельзя называть плечом диполя, как это принято в современной электродинамике.
Электрические заряды разного знака (+ q и – q) можно назвать электрическими монополями. Единичными электрическими монополями разного знака являются электроны и позитроны. У электрона и позитрона противоположны направления их орбитального движения вокруг ядра атома относительно направления их вращения вокруг собственной оси. Противоположность этих направлений и указывает на разные знаки монополей, что подробно изложено в работе В. Пакулина [2] и кратко на странице, посвященной единичным электрическим зарядам.
Теперь о магнитном диполе. Однако четкое и короткое определение для магнитного диполя, подобное тому, которое приведено выше для электрическо го диполя не найдено. Возможно, потому, что в современной физике категорически, хотя и необоснованно, говорится об отсутствии существования магнитных монополей (магнитных зарядов), которые как раз и образуют магнитный диполь. Причины такой необоснованности разъяснены в статье, посвященной магнитным зарядам. Как видно из схемы, и электрический, и магнитный диполи имеют одну и ту же структуру, разница лишь в характере заряда: статический он или динамический.
Несколько слов о магнитных зарядах. В любом замкнутом токовом контуре (а незамкнутых токовых контуров не бывает) в противоположных ветвях контура существуют заряды, названные нами токовыми зарядами (+ q и – q), являющиеся синонимами магнитных зарядов. Они равны по модулю, но разные по знаку, так как потоки зарядов (электрические токи), образующие эти токовые заряды, движутся в противоположных направлениях. В статье, посвящен- ной магнитному заряду, детально разъяснено
, что противоположно расположенные в магнитном диполе токовые заряды можно называть магнитными монополями или магнитными зарядами.
Дипольный электрический момент– это векторная физическая величина, численно равная произведению величины заряда на расстояние между ними.
|????⃗????| = ????????. (1.7)
Вектор направлен от отрицательного заряда к положительному(рис.1.7).
Напряжённость электрического поля диполя вычисляется с использованием принципа суперпозиции.
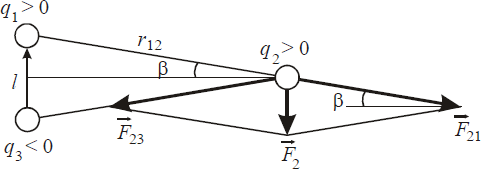
Рис.1.7. Электрическое поле диполя
Как видно из рисунка (рис.1.7.), для суммарной силы получим
????
????2 = 2????21 sin ???? = ????21????, (1.8)
21
где ????12= ????21– расстояние между зарядами ????1и ????2.
На линии, проходящей через центр диполя, перпендикулярно его оси, и на большом расстоянии rот его центра, напряженность [1]
???? =????????. (1.9)
4????????????0????3
- 1 2 3 4 5 6 7 8 9 ... 12
1.4. Моделирование электрического поля
Пусть мы хотим найти электрическое поле E(r) в точке r, создаваемое точечными зарядами
????1, ????2, … , ????????.
Поскольку поле E(r) удовлетворяет принципу суперпозиции, то выражение для него может быть записано в следующем виде (закон Кулона) [2]:
????(????) = K ∑N qi (???? − ????????), (1.10)
i=1 |r−ri|3
где ????????– координата неподвижного точечного заряда, K− константа (постоянная Кулона), зависящая от выбора системы единиц: в системе СИ
 K = 1
K = 14π????0
≈ 9 × 109Нм2/Кл2, (1.11)
ε0− диэлектрическая проницаемость вакуума.
С микроскопической точки зрения кулон – очень большая единица, например заряд электрона e ≈ 1.6×10−19 Кл. Поэтому, во многих модельных рас- четах приходится выбирать разные единицы. Следует обратить внимание, что поле Е является векторным, отсюда возникают принципиальные трудности в его изображении [2]. Один из способов – разбить пространство дискретной сет- кой, найти Е в каждом узле и начертить из этих узлов стрелки в направлении вектора Е. Однако этот способ мало что может нам дать относительно величи- ны поля Е.
Принципиальная трудность здесь – это то, что векторное поле определя- ется шестью независимыми переменными: 3 координаты точки и 3 угла, а нари- совать на двумерном экране или листе бумаги функцию 6 аргументов – прин- ципиально невозможно! Это невозможно и в случае, если задача ставится в двумерной геометрии [1].
Более наглядным способом представления векторного поля является его изображение в виде силовых линий электрического поля, которые обладают следующими свойствами [1]:
а) каждая силовая линия есть направленная линия, касательная к которой в любой точке параллельна электрическому полю в этой точке;
б) эти линии – гладкие и непрерывные, за исключением особых точек, в которых располагаются точечные заряды; силовые линии начинаются на
положительных зарядах ("источниках" поля) и заканчиваются на отрицатель- ных ("стоках");
в) полное число электрических силовых линий, выходящих из точечного заряда или входящих в него, пропорционально величине этого заряда; коэффи- циент пропорциональности выбирается из соображений наибольшей ясности при изображении поля.
Алгоритм[1]:
-
выбирается некоторая точка плоскости (х, у) и вычисляются компоненты Ex и Ey вектора электрического поля по формуле, а именно:
Ex(r) = K ∑N qi (x − xi), (1.12)
i=1 |r−ri|3
Ey(r) = K ∑N qi (y − yi), (1.13)
i=1 |r−ri|3


r = �x2 + y2,ri = �x2 + y2; (1.14)
i i
-
из этой точки проводится небольшой прямолинейный отрезок заданной длины Δs в направлении Е, компоненты которого равны:
∆x = ∆s Ex , ∆y = ∆s Ey ; (1.15)
|E| |E|
-
данная процедура повторяется с новой точки (x+Δx, y+Δy) до тех пор, по- ка силовая линия не уйдет в бесконечность (за пределы окна рисования на экране), или не подойдет к какому-нибудь отрицательному заряду.
- 1 2 3 4 5 6 7 8 9 ... 12